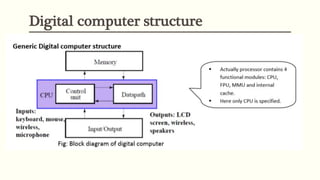
Digital systems process and store information in digital form using discrete values, usually binary digits 0 and 1. A computer manipulates information in binary form using transistors in on or off states. Digital systems are found in a wide range of applications and have advantages over analog systems like lower cost, greater reliability, and flexibility. Digital computers represent numbers, instructions, and data using binary numbers and perform arithmetic and logical operations on them.

1. Er. Nawaraj Bhandari
Digital Logic
Chapter 1: Binary System

2. Analog System
Analog systems process analog signals (continuous time signals) which
can take any value within a range, for example the output from a
speaker or a microphone

3. Digital Systems
 Digital systems are designed to store, process, and communicate
information in digital form.
 They are found in a wide range of applications, including process
control, communication systems, digital instruments, and consumer
products. The digital computer, more commonly called the computer,
is an example of a typical digital system.
 They are involved in our business transactions, communications,
transportation, medical treatment and entertainment. In industrial
world they are heavily employed in design, manufacturing, distribution
and sales.

4. Digital Systems
 Digital systems process digital signals which can take only a limited
number of values (discrete steps), usually just two values are used:
the positive supply voltage (+Vs) and zero volts (0V).
 Digital systems contain devices such as logic gates, flip-flops, shift
registers and counters.

5. Digital Systems
 A computer manipulates information in digital, or more precisely,
binary form.
 A binary number has only two discrete values — zero or one. Each
of these discrete values is represented by the OFF and ON status of
an electronic switch called a transistor.
 All computers, therefore, only understand binary numbers. Any
decimal number (base 10, with ten digits from 0 to 9) can be
represented by a binary number (base 2, with digits 0 and 1).

6. Digital computer structure

7. Digital computer structure
 Memory stores programs as well as input, output and intermediate
data
 The Datapath performs arithmetic and other data-processing
operations as specified by the program.
 The control unit supervises the flow of information between the
various units.
 A data path, when combined with the control unit, forms a
component referred to as a central processing unit, or CPU.
 The program and data prepared by the user are transferred into
memory by means of an input device such as a keyboard. An output
device, such as a CRT (cathode-ray tube) monitor, displays the results
of the computations and presents them to the user.

8. Advantages of digital system
 Have made possible many scientific, industrial, and commercial
advances that would have been unattainable otherwise.
 Less expensive
 More reliable
 Easy to manipulate
 Flexibility and Compatibility
 Information storage can be easier in digital computer systems than in
analog ones. New features can often be added to a digital system
more easily too.

9. Disadvantages of digital system
 Use more energy than analog circuits to accomplish the same tasks,
thus producing more heat as well.
 Digital circuits are often fragile, in that if a single piece of digital data
is lost or misinterpreted, the meaning of large blocks of related data
can completely change.
 Digital computer manipulates discrete elements of information by
means of a binary code

10. Binary numbers
 Binary Numbers are the flow of information in the form of zeros and
ones used by digital computers and systems

11. Binary numbers
For example: (24)10 = (?)2

12. Decimal Number System (Base-10 system)
(11010.01)2 can be interpreted using power series as:
(11010.01)2 = 1X 24 + 1 X 23 + 0 X 22 + 1 X 21 + 0 X 20 +0 X 2-1 + 1 X
2-2 = (26.25)10

13. Octal Number System (Base-8 system)
An octal numbers are expressed with a strings of symbols defined
above, possibly, an octal point within it. The decimal equivalent of a
octal number can be found by expanding the number into a power
series with a base of 8.
Example: (40712.56)8 can be interpreted using power series as:
(40712.56)8 = 4 X 84 + 0 X 83 + 7 X 82 + 1 X 81 + 2 X 80 + 5 X 8-1 + 6
X 8-2 = (16842.1)10
8-1 = {0, 1, 2…6, 7}

14. Hexadecimal Number System (Base-16
system)
A hexadecimal numbers are expressed with a strings of symbols
defined above, possibly, a hexadecimal point with in it. The decimal
equivalent of a hexadecimal number can be found by expanding the
number into a power series with a base of 16.
16-1 = {0, 1, 2…9, A, B, C, D, E, F}
(4D71B.C6)16 = 4 X 164 + D X 163 + 7 X 162 + 1 X 161 + B X 160 + C
X 16-1 + 6 X 16-2 = 4 X 164 + 13 X 163 + 7 X 162 + 1 X 161 + 11 X
160 + 12 X 16-1 + 6 X 16-2 = (317211.7734375)10

15. Number

16. Number

17. Complements
 Complements are used in digital computers for simplifying the
subtraction operation and for logical manipulation. There are two
types of complements for each base-r system.
a. r's complement
b. (r - 1)'s complement

18. Signed Binary Numbers

19. Signed Magnitude Convention

20. Signed Magnitude Convention
 The signed magnitude convention uses the left-most bit to represent
the sign (0 for positive and 1 for negative).
 The user determines whether the number is signed or unsigned
 If the binary number is signed then the leftmost bit represents the
sign and the rest of the bits represents the number
 If the binary number is unsigned then the leftmost bit is the most
significant bit of the number
 For example:
 01001 can be considered as 9 (unsigned binary) or a +9 because
the left most bit is zero.

21. Signed Complement System
 In signed Complement System, negative number is indicated by its
complement (Complement of positive number)
 Positive numbers always start with 0 (plus), its complement
(representing negative number) will always start with 1
 Signed complement system can use either 1’s complement or 2’s
complement.
 For example:
 +9 is represented only as 00001001 but –9 can be represented as:
 11110110 Signed 1’s complement representation
 11110111 Signed 2’s complement representation

22. Number Representations
 The following is the representation for +11:
 00001011
 The following are different methods for representing -11:
 Signed magnitude: 10001011
 Signed-1’s-complement: 11110100
 Signed-2’s-complement: 11110101

23. Signed Binary Numbers

24. Arithmetic Addition (Signed Magnitude
System)
 The addition of two signed binary numbers in the signed magnitude
system follows the rules of ordinary arithmetic
 If the signs are the same we add the two magnitudes and give the sum
the common sign
 If the signs are different we subtract the smaller magnitude from the
larger and give the result the sign of the larger magnitude

25. Example
 Consider the subtraction (–6) –(–13) = +7
 This subtraction is changed to addition by taking 2’s complement of
the subtrahend (– 13) to give (+ 13)
 In binary this is 11010 + 01101 = 1 00111
 Removing the end carry, we obtain the correct answer: 00111(+7)

26. Example
 Let us perform the subtraction of two decimal numbers +4 and +7 using 2’s
complement method.
 The subtraction of these two numbers is
 (+4)10 − (+7)10 = (+4)10 + (−7)10.
 The 2’s complement representation of +4 and -7 with 5 bits each are shown below.
 (+4)10 = (00100)2
 (-7)10 = (11001)2
 ⇒(+4)10 + (-7)10 = (00100)2 + (11001)2 = (11101)2
 Here, carry is not obtained from sign bit. The sign bit ‘1’ indicates that the resultant sum
is negative. So, by taking 2’s complement of it we will get the magnitude of resultant sum
as 3 in decimal number system. Therefore, subtraction of two decimal numbers +4 and
+7 is -3.

27. Binary Codes for Decimal digits(BCD)

28. BCD:8421
 The weights of this code are 8, 4, 2 and 1.
 This code has all positive weights. So, it is a positively weighted code.
 This code is also called as natural BCD (Binary Coded Decimal) code.
 Example
 Let us find the BCD equivalent of the decimal number 786. This
number has 3 decimal digits 7, 8 and 6. From the table, we can write
the BCD (8421) codes of 7, 8 and 6 are 0111, 1000 and 0110
respectively.
 ∴ (786)10 = (011110000110)BCD

29. 2 4 2 1 code
oThe weights of this code are 2, 4, 2 and 1.
oThis code has all positive weights. So, it is a positively
weighted code.
oIT is a self-complementing code. Self-complementing codes
provides the 9’s complement of a decimal number.

30. 2 4 2 1 code
 Example
 Let us find the 2421 equivalent of the decimal number 786.
This number has 3 decimal digits 7, 8 and 6. From the table,
we can write the 2421 codes of 7, 8 and 6 are 1101, 1110 and
1100 respectively.
 Therefore, the 2421 equivalent of the decimal number 786 is
110111101100.

31. 8 4 -2 -1 code
 The weights of this code are 8, 4, -2 and -1.
 This code has negative weights along with positive weights. So, it is a
negatively weighted code.
 It is a self-complementing code.

32. 8 4 -2 -1 code
Example
 Let us find the 8 4-2-1 equivalent of the decimal number 786. This
number has 3 decimal digits 7, 8 and 6. From the table, we can write
the 8 4 -2 -1 codes of 7, 8 and 6 are 1001, 1000 and 1010
respectively.
 Therefore, the 8 4 -2 -1 equivalent of the decimal number 786 is
100110001010.

33. Excess 3 code
 We will get the Excess 3 code of a decimal number by adding
three(0011) to the binary equivalent of that decimal number. Hence, it
is called as Excess 3 code.
 It is a self-Complementing code.

34. Excess 3 code
Example
 Let us find the Excess 3 equivalent of the decimal number 786. This
number has 3 decimal digits 7, 8 and 6. From the table, we can write
the Excess 3 codes of 7, 8 and 6 are 1010, 1011 and 1001
respectively.
 Therefore, the Excess 3 equivalent of the decimal number 786 is
101010111001

35. Gray Code
 A numerical code used in computing in which consecutive integers are
represented by binary numbers differing in only one digit.
 Binary code to Gray Code Conversion
Follow these steps for converting a binary code into its equivalent Gray code.
 Consider the given binary code and place a zero to the left of MSB.
 Compare the successive two bits starting from zero. If the 2 bits are same, then
the output is zero. Otherwise, output is one.
 Repeat the above step till the LSB of Gray code is obtained.

36. Gray Code

37. Gray Code
Example
 From the table, we know that the Gray code corresponding to binary
code 1000 is 1100. Now, let us verify it by using the above procedure.
 Given, binary code is 1000.
 Step 1 − By placing same to the left of MSB, the MSB is 1.
 Step 2 − By comparing successive two bits of new binary code, we
will get the gray code as 1100.

38. ANY QUESTIONS?