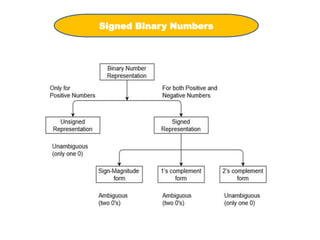
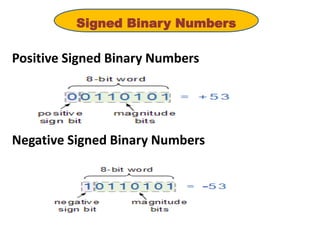
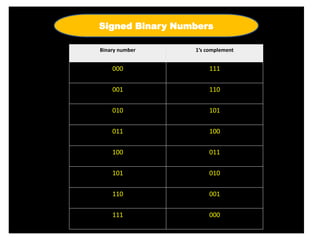
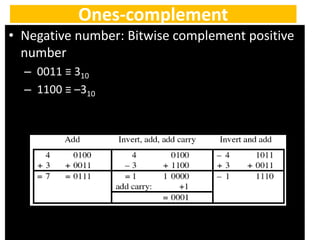
The document discusses different methods for representing signed binary numbers: 1) Sign-magnitude notation represents positive and negative numbers by using the most significant bit to indicate the sign (0 for positive, 1 for negative) and the remaining bits for the magnitude. 2) One's complement represents negative numbers by inverting all bits of the positive number. 3) Two's complement, the most common method, represents negative numbers by inverting all bits and adding 1 to the result. This allows simple addition to perform subtraction.

1. Dr.M.Pyingkodi
AP/MCA
Kongu Engineering College
Erode, Tamilnadu
Signed Binary Numbers

2. • Both positive and negative numbers may be represented.
• The most significant bit represents the sign
• Three main signed binary number codes are used.
– Sign magnitude
– 2s complement
– 1s complement
• Sign-magnitude notation is the simplest and one of the
most common methods of representing positive and
negative numbers either side of zero, (0).
• for example, +2 and -2, +10 and -10, etc.
• If the sign bit is “0”, this means the number is positive in
value. If the sign bit is “1”, then the number is negative in
value.
Signed Binary Numbers

3. Signed Binary Numbers

4. Positive Signed Binary Numbers
Negative Signed Binary Numbers
Signed Binary Numbers

5. 1) -5610 as a 8-bit number
101110002
2) 8510 as a 8-bit number
010101012
3) -12710
111111112
Signed Binary Numbers

6. • Unsigned numbers don’t have any sign
• Contain only magnitude of the number.
Representation of unsigned binary numbers are all
positive numbers only.
• For example, representation of positive decimal
numbers are positive by default.
• We always assume that there is a positive sign symbol
in front of every number.
Unsigned Numbers

7. • Signed numbers contain sign flag, this representation
distinguish positive and negative numbers
• For example, in representation of negative decimal numbers,
we need to put negative symbol in front of given decimal
number.
Representation of Signed Binary Numbers:
– Sign-Magnitude form
– 1’s complement form
– 2’s complement form
Signed Binary Numbers

8. • For n bit binary number,
• 1 bit is reserved for sign symbol.
• If the value of sign bit is 0, then the given number will be
positive,
• else if the value of sign bit is 1, then the given number will be
negative.
• Remaining (n-1) bits represent magnitude of the number.
• The positive number is simply represented as a magnitude
form.
Sign-Magnitude form

9. • 1’s complement of a number is obtained by
inverting each bit of given number.
• method which we can use to represent
negative binary numbers in a signed binary
number system.
• the one’s complement of “1” is “0” and vice
versa, then the one’s complement
of 100101002 is simply 011010112 as all the 1’s
are changed to 0’s and the 0’s to 1’s.
1’s complement form

10. Signed Binary Numbers
Binary number 1’s complement
000 111
001 110
010 101
011 100
100 011
101 010
110 001
111 000

11. • Negative number: Bitwise complement positive
number
– 0011 ≡ 310
– 1100 ≡ –310
Why 1’s complement

12. Ones-complement
• Negative number: Bitwise complement positive
number
– 0011 ≡ 310
– 1100 ≡ –310
• Solves th arithmetic problem

13. • Binary subtraction is very much difficult as
compare to addition.
• To do subtraction
• first the binary number subtracted from
another number is represented in 1s
complemented form and then add with the
another number.
Why 1’s complement

14. • To get 2’s complement of a binary number, simply invert the
given number and add 1 to the least significant bit (LSB) of
given result.
• performing arithmetic operations such as subtraction, addition
2’s complement