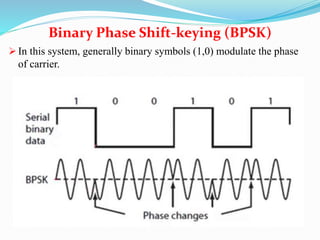
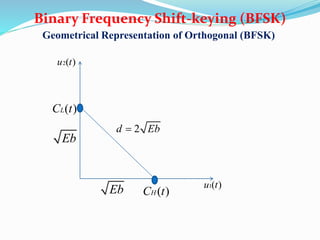
This document discusses various digital modulation techniques including: - Coherent and non-coherent detection methods for baseband and broadband signals - Phase-locked loops used in frequency demodulation - Digital modulation techniques where binary symbols modulate the carrier phase, including BPSK where the carrier phase is shifted by 180 degrees to represent 1s and 0s - BFSK where the carrier frequency is shifted according to the binary symbols while keeping the phase unchanged - ASK where the carrier amplitude is shifted according to the binary symbols to keep the frequency constant - Pulse modulation techniques where pulse amplitude, width, or time is varied to transmit analog data.

1. Instructor
Engr. Muhammad Yaseen

2.  Baseband Transmission.
 Broadband Transmission / Pass-band Transmission.
Coherent (Synchronous) Detection
 In this method, the local carrier generated at the receiver is phase
locked with carrier at the transmitter.
Non-Coherent (Envelop) Detection
 In this method, the receiver carrier need not be phase locked with
transmitter carrier.
Phase-Locked Loop (PLL)
 A frequency-or phase-sensitive feedback control circuit used in
frequency demodulation. frequency synthesizers, and various
filtering and signal detection applications.
Digital Modulation Techniques

3.  In this system, generally binary symbols (1,0) modulate the phase
of carrier.
Binary Phase Shift-keying (BPSK)

4. Let the carrier be:
A→ Peak value of sinusoidal carrier
1Ω→ Load resistor
Then, Power dissipated:
 When symbol will change then phase of the carrier signal changed in 1800
If,
Binary Phase Shift-keying (BPSK)
c( ) cos2 t--------------(1)c t Ac f
21
2
2
P A
A P


1
2
1 ( ) 2 cos(2 )
0 ( ) 2 cos(2 )
c
c
C t P f t
C t P f t

 
 
  

5. Then (BPSK) combine signal will be:
b(t) = +1 when binary 1 is transmitted
b(t) = -1 when binary 0 is transmitted
Geometrical Representation of (BPSK) signal
Orthogonal carrier signal
Binary Phase Shift-keying (BPSK)
( ) ( ) 2 cos(2 )cC t b t P f t
cos( ) cos    
1
1
( ) ( ) 2 cos(2 )
2
( ) ( ) . cos(2 )
2
, ( ) cos(2 )
( ) ( ) . ( )
c
c
c
C t b t P f t
C t b t P Tb f t
Tb
let t f t
Tb
C t b t P Tb t


 


 
    
 

6. Bit energy
 If d increases then probability of signal error will be will be
decreased and vice versa.
 Band width of (BPSK)
Binary Phase Shift-keying (BPSK)
.Eb PTb
1( ) . ( )
( ) 1
C t Eb t
b t
 
  
1( )t
Eb Eb
2d Eb
Represents
symbol (0)
Represents
symbol (1)
. 2 bBW f

7.  In this system, generally binary symbols (1,0) modulate the
frequency of carrier. And phase will be un-effected.
OR
 In this system, it shifts the frequency of carrier signal according to
the binary symbols (1,0) and phase will be un-effected.
Binary Frequency Shift-keying (BFSK)

8. Mathematical representation of BFSK
Here,
According to logic level 1 and 0
Binary Frequency Shift-keying (BFSK)
 ( ) 2 cos ( )
( ) 1 1
( ) 2 cos( )
( ) 2 cos( )
( ) ( )
( )
( )
BFSK o
H o
L o
o o
H o
L o
V t P t d t t
d t or
C t P t
C t P t
or



 
 
 
  
  
  
 
  
  
 
Angular Frequency
Higher Frequency
Lower Frequency

9. Geometrical Representation of Orthogonal (BFSK)
Binary Frequency Shift-keying (BFSK)
2d Eb
Eb
Eb ( )HC t
( )LC t
1( )u t
2( )u t

10.  In this system, generally binary symbols (1,0) modulate the
amplitude of the carrier. It is also known as on-off keying (ook)
OR
 In this system, it shifts the amplitude of carrier signal according to
the binary symbols (1,0) and frequency will be constant.
Amplitude Shift-keying (ASK)

11.  Modulation used to transmit analog data in the form of pulses
whose amplitude, width, or time portion is varied.
Pulse Modulation (PM)