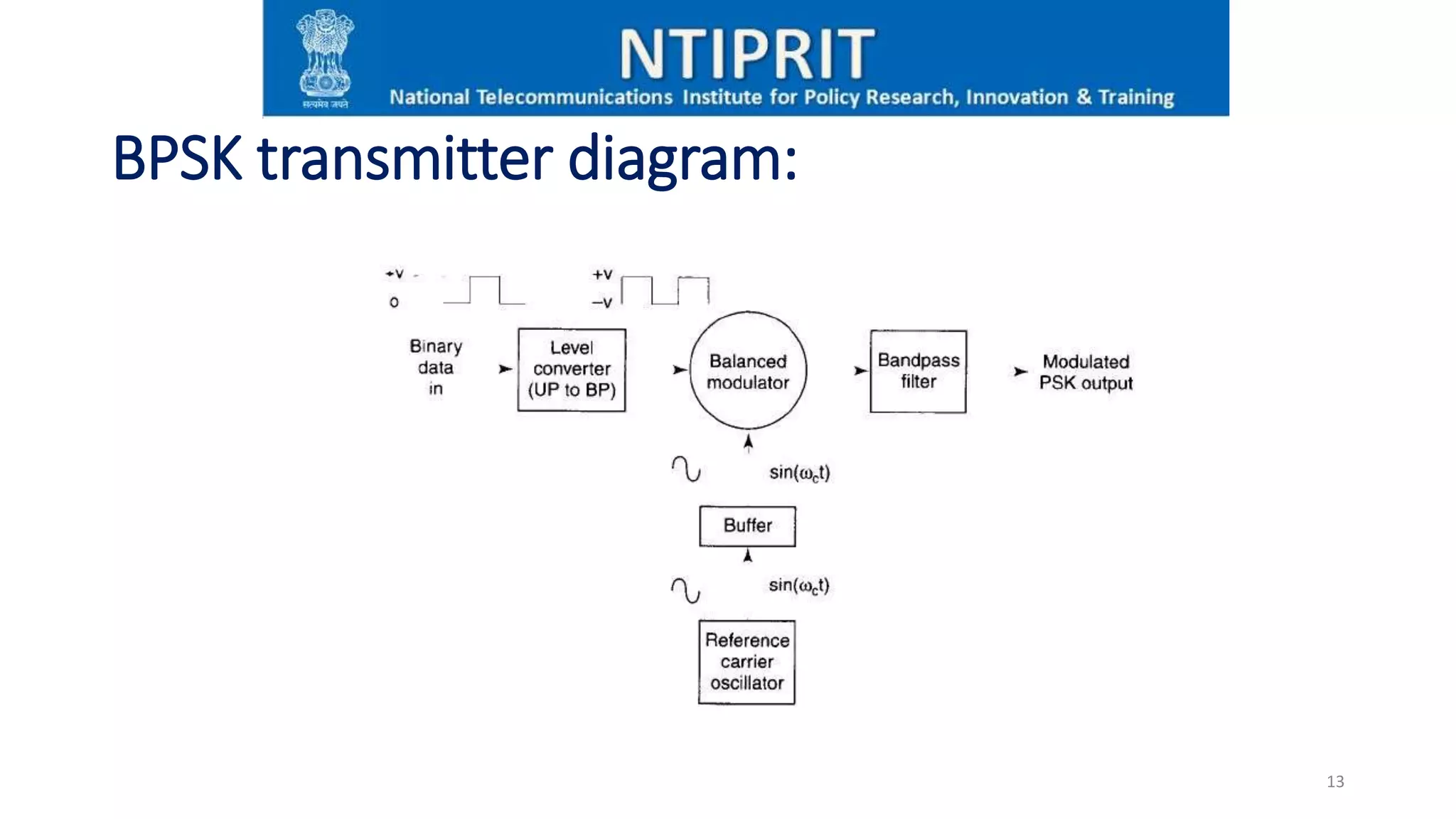
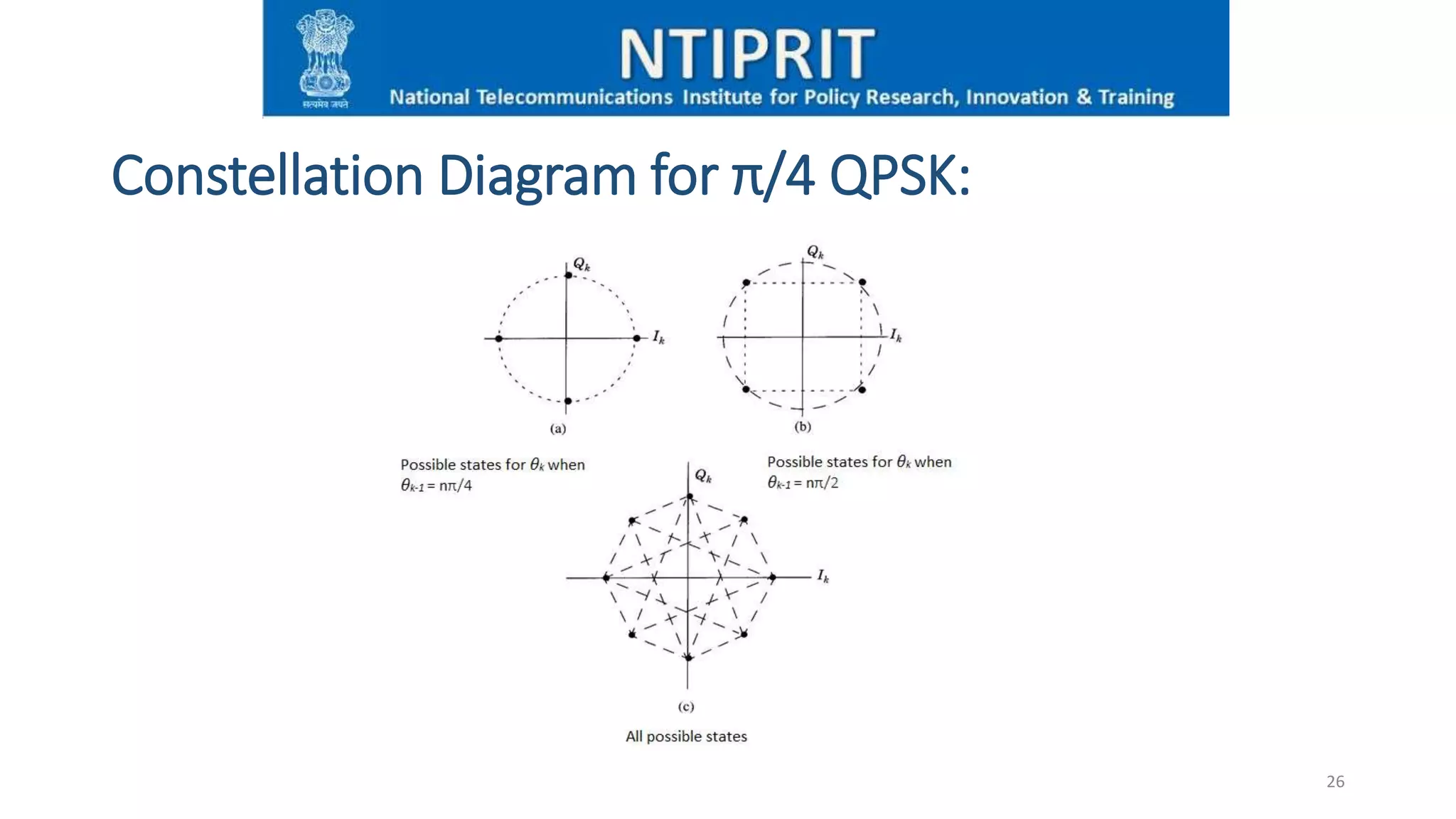
The presentation covers digital communication concepts and phase shift keying (PSK), including binary PSK (BPSK) and π/4-quadrature PSK (QPSK). It explains their modulation techniques, advantages, disadvantages, and applications, highlighting the significance of bandwidth and information capacity. The document also details the design of BPSK transmitters and receivers, along with alternative PSK schemes like 8-PSK and QAM.

1. Phase Shift Keying &
π/4 -Quadrature Phase Shift
Keying
Presentation by:
Naveen Jakhar, ITS
1

2. Topics covered in this presentation:
 Some basic definitions & concepts of digital communication
What is Phase Shift Keying(PSK) ?
Binary Phase Shift Keying – BPSK
BPSK transmitter & receiver
Advantages & Disadvantages of BPSK
Pi/4 – QPSK
Pi/4 – QPSK transmitter & receiver
Advantages of Pi/4- QPSK
2

3. Some basic concepts of Digital Communication:
Information capacity: linear function of bandwidth and transmission
time i.e. 𝐼 ∝ 𝐵 × 𝑡
where I is information capacity(bits per second)
B is bandwidth (hertz)
t is transmission time (sec)
 Shannon limit for information capacity
𝐼 = 𝐵 log2(1 + 𝑆𝑁𝑅)
Where SNR is signal to noise power ratio (unit less quantity)
3

4. M-ary coding:
M-ary is a term derived from binary
M represents a digit that corresponds to the number of conditions,
levels, or combinations possible for a given number of binary
variables, for e.g. a digital signal with four possible conditions (voltage
levels, frequencies, phases) is an M-ary system where M = 4
Number of bits necessary to produce a given number of conditions is
expressed mathematically as 𝑁 = log2 𝑀 or 2 𝑁 = 𝑀 where N is
number of necessary bits & M is number of
conditions/combinations/levels
4

5. Baud and Minimum bandwidth:
Baud or symbols per second- rate of change of a signal on the
transmission medium after encoding and modulation have occurred
Baud is a unit of transmission rate, modulation rate or symbol rate
𝐵𝑎𝑢𝑑 =
1
𝑡 𝑠
where 𝑡 𝑠is time of one signalling element (seconds)
Minimum theoretical bandwidth necessary to propagate a signal is
called the minimum Nyquist bandwidth or minimum Nyquist
frequency. Thus,𝑓𝑏 = 𝐵, where 𝑓𝑏 is the bit rate in bits per second
and B is the ideal Nyquist bandwidth.
5

6. Baud and Minimum bandwidth: continued ….
 The relationship between bandwidth and bit rate also applies to the
opposite situation. For a given bandwidth (B), the highest theoretical
bit rate is 2B.
Using multilevel signalling, the Nyquist formula for channel capacity
is 𝑓𝑏 = 𝐵log2 𝑀 or 𝑓𝑏 = 𝐵 × 𝑁 => 𝐵 =
𝑓 𝑏
𝑁
where 𝑓𝑏 is channel capacity in bits per second, B is minimum Nyquist
bandwidth and M is number of discrete signal or voltage levels
𝐵𝑎𝑢𝑑 =
𝑓 𝑏
𝑁
, so Baud is also the bit rate divided by the number of bits
encoded into one signalling element
6

7. Phase Shift Keying (PSK): Introduction
PSK is a digital modulation scheme which conveys data by
changing/modulating the phase of the carrier signal
Phase of carrier signal is varied in proportional to the information
signal
The carrier signal is also called reference signal
The modulation is done by varying sine and cosine inputs at a precise
time
PSK is often called angle modulated constant amplitude digital
modulation
Simplest form of PSK is Binary phase shift keying (BPSK)
7

8. Binary Phase Shift Keying (BPSK):
BPSK has values of N=1 and M=2, so two phases for the carrier are
possible
One phase represents a logic 1 and the other phase represents a logic
0. As the input digital signal changes state (i.e., 1 -> 0 or 0 -> 1), the
phase of the output carrier shifts between two angles that are
separated by 180°
8

9. Binary Phase Shift Keying (BPSK): continued …..
 Any carrier signal is s(t) = A cos (2π𝑓𝑐t +θ) where θ is the phase
For BPSK, we have θ=0 or θ=π, separated by 180 degrees
So, the BPSK signals become A m(t)cos (2π𝑓𝑐t +θ)
𝑣1 𝑡 = Acos2π𝑓𝑐 𝑡 0 ≤ t ≤ T, for 1 and
𝑣2 𝑡 = −Acos2π𝑓𝑐 𝑡 0 ≤ t ≤ T, for 0
where A is a constant, 𝑓𝑐is the carrier frequency and T is the bit
duration
 The signal has a power 𝑃 =
𝐴2
2
means 𝐴 = 2𝑃
9

10. Binary Phase Shift Keying (BPSK): continued …..
So, the signals 𝑣1,2 𝑡 = ±Acos2π𝑓𝑐 𝑡 becomes
𝑣1,2 𝑡 = ± 2𝑃cos2π𝑓𝑐 𝑡
= ± 𝑃𝑇
2
𝑇
cos2π𝑓𝑐 𝑡
= ± 𝐸
2
𝑇
cos2π𝑓𝑐 𝑡
where E=P*T is the energy contained in a bit duration.
ᶲ1,2 𝑡 = ±
2
𝑇
cos2π𝑓𝑐 𝑡 are the orthonormal functions with unit
energy in a bit duration
10

11. BPSK Constellation Diagram
 Constellation points are drawn on a
2 dimensional complex co-ordinate
system
ᶲ1 𝑡 =
2
𝑇
cos2π𝑓𝑐 𝑡 0 ≤ t ≤ T
ᶲ2 𝑡 = −
2
𝑇
sin2π𝑓𝑐 𝑡 0 ≤ t ≤ T
11

12. BPSK transmitter:
Other names for BPSK are phase reversal keying (PRK) and biphase
modulation
BPSK is a form of square-wave modulation of a continuous wave (CW)
signal
Important components of a BPSK transmitter are : Balanced
modulator, level converter, Band pass filter and Reference Carrier
Oscillator
Balanced modulator acts as a phase reversing switch
Another name of Balanced modulator is Balanced Ring modulator
12

13. BPSK transmitter diagram:
13

14. BPSK Balanced Ring Modulator:
The balanced modulator has two inputs: (1) a carrier which is in
phase with the reference oscillator and (2) the binary digital data
For the balanced modulator to operate properly, the digital input
voltage must be much greater than the peak carrier voltage
14

15. BPSK Balanced Ring Modulator Function:
When the binary input logic is 1 When the binary input logic is 0
15

16. Output of a BPSK waveform:
Logic 1 input produces an analog output signal with a 0°phase angle,
and a logic 0 input produces an analog output signal with a 180°
phase angle
16

17. BPSK Receiver:
Input signal to receiver maybe +𝑠𝑖𝑛𝜔𝑐 𝑡 or - 𝑠𝑖𝑛𝜔𝑐 𝑡
The coherent carrier recovery circuit detects and regenerates a
carrier signal that is both frequency and phase coherent with the
original transmit carrier
The balanced modulator is a product detector; the output is the
product of the two inputs (the BPSK signal and the recovered carrier)
The low-pass filter (LPF) separates the recovered binary data from
the complex demodulated signal
Coherent BPSK requires that the reference signal at the receiver to be
synchronized in phase and frequency with the received signal
17

18. BPSK Receiver output:
18
For a BPSK input signal of +𝑠𝑖𝑛𝜔𝑐 𝑡 (logic 1), the output of the
balanced modulator is:
output = (𝑠𝑖𝑛𝜔𝑐 𝑡 )(𝑠𝑖𝑛𝜔𝑐 𝑡 ) = 𝑠𝑖𝑛2
𝑤𝑐 𝑡
Now 𝑠𝑖𝑛2 𝑤𝑐 𝑡 = 0.5(1 –𝑐𝑜𝑠2𝜔𝑐 𝑡 ) = 0.5 - 0.5 𝑐𝑜𝑠2𝜔𝑐 𝑡
output = + 0.5 V = logic 1
filtered out

19. Advantages and Disadvantages of BPSK:
Advantages
The bit error rate is least in case
of BPSK due to the presence of a
spacing of 2 𝐸 between the
points on the constellation
diagram
BPSK requires half the
transmission energy for the
same bit error rate as in FSK and
ASK
Disadvantages
Costly due to use of Costas
square loop or Costas PLL in
coherent demodulation
The abrupt change of phase in
time domain is an impulse
function which requires infinite
bandwidth for transmission in
frequency domain
19

20. Applications of BPSK:
BPSK is widely used for wireless LANs, RFID and Bluetooth
communication
BPSK is used in radio communications due to robust BER
20

21. Other types of Phase Shift Keying:
QPSK - Quadrature Phase Shift Keying
π/4-QPSK - Quadrature Phase Shift Keying
O-QPSK - Offset Quadrature Phase Shift Keying
8 PSK - 8 Point Phase Shift Keying
16 PSK - 16 Point Phase Shift Keying
QAM - Quadrature Amplitude Modulation
16 QAM - 16 Point Quadrature Amplitude Modulation
64 QAM - 64 Point Quadrature Amplitude Modulation
21

22. QPSK- Quadrature Phase Shift Keying
 Four different phase states in one symbol period
 Two bits of information are transmitted in each symbol
 Twice the bandwidth efficiency of the BPSK
Phase: 0 π/2 π 3π/2 → possible phase values
Symbol: 00 01 11 10
The QPSK signal is given by, s(t) =
2Es
𝑇
cos (2π𝑓𝑐t +(i-1) π/2)
0 ≤ t ≤ T, i=1,2,3,4
22

23. QPSK Constellation Diagram
23
Now we have two basic functions
Es = 2 Eb since 2 bits are transmitted per symbol
I = in-phase component from sI(t).
Q = quadrature component that is sQ(t).

24. QPSK Bit Error Rate:
24
BER is related to the distance between constellation points

25. π/4 -QPSK :
25
 In π/4 QPSK, the maximum phase change is limited to ± 135o , as
compared to 180o for QPSK
 Hence the signal preserves the constant envelop property better
than the band limited QPSK
 This can be demodulated in a coherent or non-coherent fashion
thereby, simplifying the receiver design greatly
 In presence of multipath spread and fading, π/4 QPSK is found to
perform better

26. Constellation Diagram for π/4 QPSK:
26

27. QPSK Transmission Technique:
27

28. π/4 QPSK phase components:
28
Ik = 𝑐𝑜𝑠θk = Ik-1 𝑐𝑜𝑠ϕk - Qk-1 𝑠𝑖𝑛ϕk
Qk = 𝑠𝑖𝑛θk = Ik-1 𝑠𝑖𝑛ϕk + Qk-1 𝑐𝑜𝑠ϕk
where,
Θk = θk -1 + ϕk
θk and θk -1 are the phases of the kth and (k-1)st symbols
The phase shift ϕk is related to the input symbols mik and mqk

29. π/4 QPSK mathematical analysis:
29
The waveform is represented by:
S(t)= I(t) cos𝜔𝑐 𝑡 – Q(t) 𝑠𝑖𝑛𝜔𝑐 𝑡
where,
I 𝑡 = 𝑘=0
𝑁−1
𝐼k p(t - kTs - Ts /2) = 𝑘=0
𝑁−1
𝑐𝑜𝑠Ɵk p(t - kTs - Ts /2)
Q 𝑡 = 𝑘=0
𝑁−1
𝑄k p(t - kTs - Ts /2) = 𝑘=0
𝑁−1
𝑠𝑖𝑛Ɵk p(t - kTs - Ts /2)

30. π/4 QPSK FM Discriminator Detection
30

31. Advantages of π/4- QPSK:
 Among all MPSK schemes, QPSK is the most-often-used scheme
since it does not suffer from BER degradation while the bandwidth
efficiency is increased
In the presence of the multipath spread and fading conditions, pi/4
QPSK performs the best
Signal is demodulated in coherent and non-coherent fashion and
hence the design of the receiver is simple
31

32. Thank You
An efficient Telecommunications network is the
foundation
upon which an information society is built
32