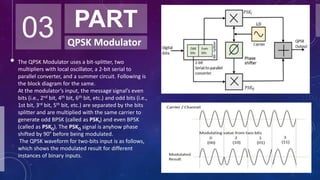
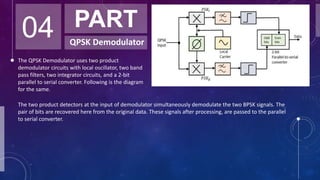
Quadrature Phase Shift Keying (QPSK) is a digital modulation scheme that transmits two bits of information at a time, effectively doubling the data rate compared to Binary Phase Shift Keying (BPSK) while requiring half the bandwidth. QPSK uses four distinct phase shifts to encode data, making it more efficient and robust for various wireless communication standards like GSM, CDMA, and LTE. The document discusses the modulation and demodulation process, technical implementation using MATLAB, and concludes by highlighting QPSK's advantages over BPSK in data transmission.

1. Quadrature
Phase
Shift Keying
SNEHESH DUTTA 11500317052
SINJON NATH 11500317053
SIDDHARTHA VYAS 11500317052

2. 01 PART
ABSTRACT
The Quadrature Phase Shift Keying QPSK is a variation of
BPSK, and it is also a Double Side Band Suppressed Carrier
DSBSC modulation scheme, which sends two bits of digital
information at a time, called as bigits.Instead of the
conversion of digital bits into a series of digital stream, it
converts them into bit pairs. This decreases the data bit rate
to half, which allows space for the other users.QPSK
(Quadrature Phase Shift Keying) is type of phase shift keying.
Unlike BPSK which is a DSBCS modulation scheme with digital
information for the message, QPSK is also a DSBCS
modulation scheme but it sends two bits of digital
information a time (without the use of another carrier
frequency).The amount of radio frequency spectrum required
to transmit QPSK reliably is half that required for BPSK signals,
which in turn makes room for more users on the channel.
The figure below shows a QPSK modulated waveform.

3. 02 PART
INTRODUCTION
This technical brief covers the basic characteristics of a digital modulation scheme known as
quadrature phase shift keying.
In the world of wired electronics, analog signals exhibit continuous variations whereas digital signals
assume (ideally) one of two discrete states. This distinction can be extended to systems that transmit
data via electromagnetic radiation instead of electric current traveling through wires.
When used for analog signals, frequency modulation and amplitude modulation lead to continuous
variations in the frequency or amplitude of a carrier wave. When modulation techniques are used for
digital communication, the variations applied to the carrier are restricted according to the discrete
information being transmitted.
Examples of common digital modulation types are OOK (on/off keying), ASK (amplitude shift keying),
and FSK (frequency shift keying). These schemes cause the carrier to assume one of two possible
states depending on whether the system must transmit a binary 1 or a binary 0; each discrete carrier
state is referred to as a symbol.

4. Quadrature phase shift keying (QPSK) is another modulation technique, and it’s a
particularly interesting one because it actually transmits two bits per symbol. In
other words, a QPSK symbol doesn’t represent 0 or 1—it represents 00, 01, 10, or
11.
This two-bits-per-symbol performance is possible because the carrier variations are
not limited to two states. In ASK, for example, the carrier amplitude is either
amplitude option A (representing a 1) or amplitude option B (representing a 0). In
QPSK, the carrier varies in terms of phase, not frequency, and there are four possible
phase shifts.
We can intuitively determine what these four possible phase shifts should be: First
we recall that modulation is only the beginning of the communication process; the
receiver needs to be able to extract the original information from the modulated
signal. Next, it makes sense to seek maximum separation between the four phase
options, so that the receiver has less difficulty distinguishing one state from another.
We have 360° of phase to work with and four phase states, and thus the separation
should be 360°/4 = 90°. So our four QPSK phase shifts are 45°, 135°, 225°, and 315°.

5. 03 PART
QPSK Modulator
The QPSK Modulator uses a bit-splitter, two
multipliers with local oscillator, a 2-bit serial to
parallel converter, and a summer circuit. Following is
the block diagram for the same.
At the modulator’s input, the message signal’s even
bits (i.e., 2nd bit, 4th bit, 6th bit, etc.) and odd bits (i.e.,
1st bit, 3rd bit, 5th bit, etc.) are separated by the bits
splitter and are multiplied with the same carrier to
generate odd BPSK (called as PSKI) and even BPSK
(called as PSKQ). The PSKQ signal is anyhow phase
shifted by 90° before being modulated.
The QPSK waveform for two-bits input is as follows,
which shows the modulated result for different
instances of binary inputs.

6. 04 PART
QPSK Demodulator
The QPSK Demodulator uses two product
demodulator circuits with local oscillator, two band
pass filters, two integrator circuits, and a 2-bit
parallel to serial converter. Following is the diagram
for the same.
The two product detectors at the input of demodulator simultaneously demodulate the two BPSK signals. The
pair of bits are recovered here from the original data. These signals after processing, are passed to the parallel
to serial converter.

7. 05 PART
QPSK Modulation Applications
Similar to BPSK, QPSK is used in various cellular wireless standards such as GSM, CDMA, LTE, 802.11 WLAN,
802.16 fixed and mobile WiMAX, Satellite and CABLE TV applications.
• As difference between any two constellation point is 90 degree maximum, QPSK modulation type has many
benefits. It is robust compare to other modulation techniques except BPSK.
• It has double data rate carrying capacity compare to BPSK as two bits are mapped on each constellation points.
In BPSK only 1 bit is mapped to each constellation point.

8. 06 PART
MATLAB Code for QPSK
Modulation and Demodulation
clc;
clear all;
close all;
data=[0 1 0 1 1 1 0 0 1 1]; % information
%Number_of_bit=1024;
%data=randint(Number_of_bit,1);
figure(1)
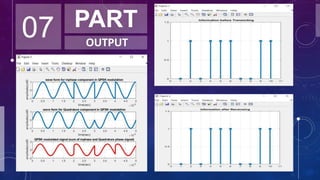
stem(data, 'linewidth',3), grid on;
title(' Information before Transmiting ');
axis([ 0 11 0 1.5]);
data_NZR=2*data-1; % Data Represented at NZR form for QPSK modulation
s_p_data=reshape(data_NZR,2,length(data)/2); % S/P convertion of data
br=10.^6; %Let us transmission bit rate 1000000
f=br; % minimum carrier frequency
T=1/br; % bit duration
t=T/99:T/99:T; % Time vector for one bit information
% XXXXXXXXXXXXXXXXXXXXXXX QPSK modulation XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

9. y=[];
y_in=[];
y_qd=[];
for(i=1:length(data)/2)
y1=s_p_data(1,i)*cos(2*pi*f*t); % inphase component
y2=s_p_data(2,i)*sin(2*pi*f*t) ;% Quadrature component
y_in=[y_in y1]; % inphase signal vector
y_qd=[y_qd y2]; %quadrature signal vector
y=[y y1+y2]; % modulated signal vector
end
Tx_sig=y; % transmitting signal after modulation
tt=T/99:T/99:(T*length(data))/2;
figure(2)
subplot(3,1,1);
plot(tt,y_in,'linewidth',3), grid on;
title(' wave form for inphase component in QPSK modulation ');
xlabel('time(sec)');
ylabel(' amplitude(volt0');
subplot(3,1,2);
plot(tt,y_qd,'linewidth',3), grid on;
title(' wave form for Quadrature component in QPSK modulation ');
xlabel('time(sec)');

10. ylabel(' amplitude(volt0');
subplot(3,1,3);
plot(tt,Tx_sig,'r','linewidth',3), grid on;
title('QPSK modulated signal (sum of inphase and Quadrature phase signal)');
xlabel('time(sec)');
ylabel(' amplitude(volt0');
% XXXXXXXXXXXXXXXXXXXXXXXXXXXX QPSK demodulation XXXXXXXXXXXXXXXXXXXXXXXXXX
Rx_data=[];
Rx_sig=Tx_sig; % Received signal
for(i=1:1:length(data)/2)
%%XXXXXX inphase coherent dector XXXXXXX
Z_in=Rx_sig((i-1)*length(t)+1:i*length(t)).*cos(2*pi*f*t);
% above line indicat multiplication of received & inphase carred signal
Z_in_intg=(trapz(t,Z_in))*(2/T);% integration using trapizodial rull
if(Z_in_intg>0) % Decession Maker
Rx_in_data=1;
else
Rx_in_data=0;
end

11. %%XXXXXX Quadrature coherent dector XXXXXX
Z_qd=Rx_sig((i-1)*length(t)+1:i*length(t)).*sin(2*pi*f*t);
%above line indicat multiplication ofreceived & Quadphase carred signal
Z_qd_intg=(trapz(t,Z_qd))*(2/T);%integration using trapizodial rull
if (Z_qd_intg>0)% Decession Maker
Rx_qd_data=1;
else
Rx_qd_data=0;
end
Rx_data=[Rx_data Rx_in_data Rx_qd_data]; % Received Data vector
end
figure(3)
stem(Rx_data,'linewidth',3)
title('Information after Receiveing ');
axis([ 0 11 0 1.5]), grid on;

12. 07 PART
OUTPUT

13. 08 PART
CONCLUSION
The mathematical analysis shows that QPSK can be used either to double the data rate compared
with a BPSK system while maintaining the same bandwidth of the signal, or to maintain the data-rate
of BPSK but halving the bandwidth needed. In this latter case, the BER of QPSK is exactly the same as
the BER of BPSK – and deciding differently is a common confusion when considering or describing
QPSK. The transmitted carrier can undergo numbers of phase changes.
Given that radio communication channels are allocated by agencies such as the Federal
Communications Commission giving a prescribed (maximum) bandwidth, the advantage of QPSK over
BPSK becomes evident: QPSK transmits twice the data rate in a given bandwidth compared to BPSK -
at the same BER. The engineering penalty that is paid is that QPSK transmitters and receivers are
more complicated than the ones for BPSK. However, with modern electronics technology, the penalty
in cost is very moderate.
As with BPSK, there are phase ambiguity problems at the receiving end, and differentially encoded
QPSK is often used in practice.

14. 09 PART
REFERANCES
1. www.google.com
2. https://www.tutorialspoint.com/
3. https://www.allaboutcircuits.com/
4. http://vlab.amrita.edu/
5. https://en.wikipedia.org/

15. Thanks For Watching