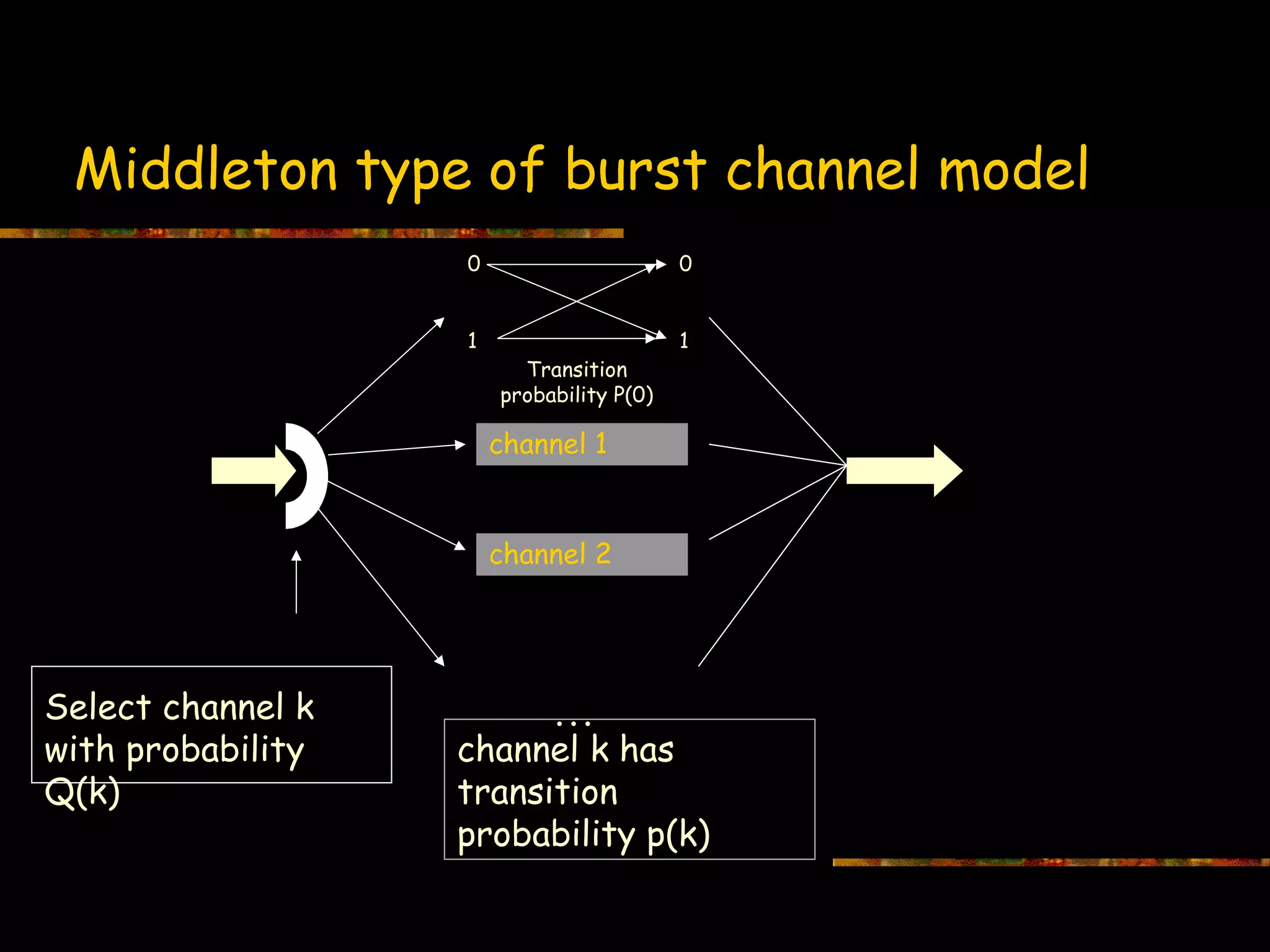
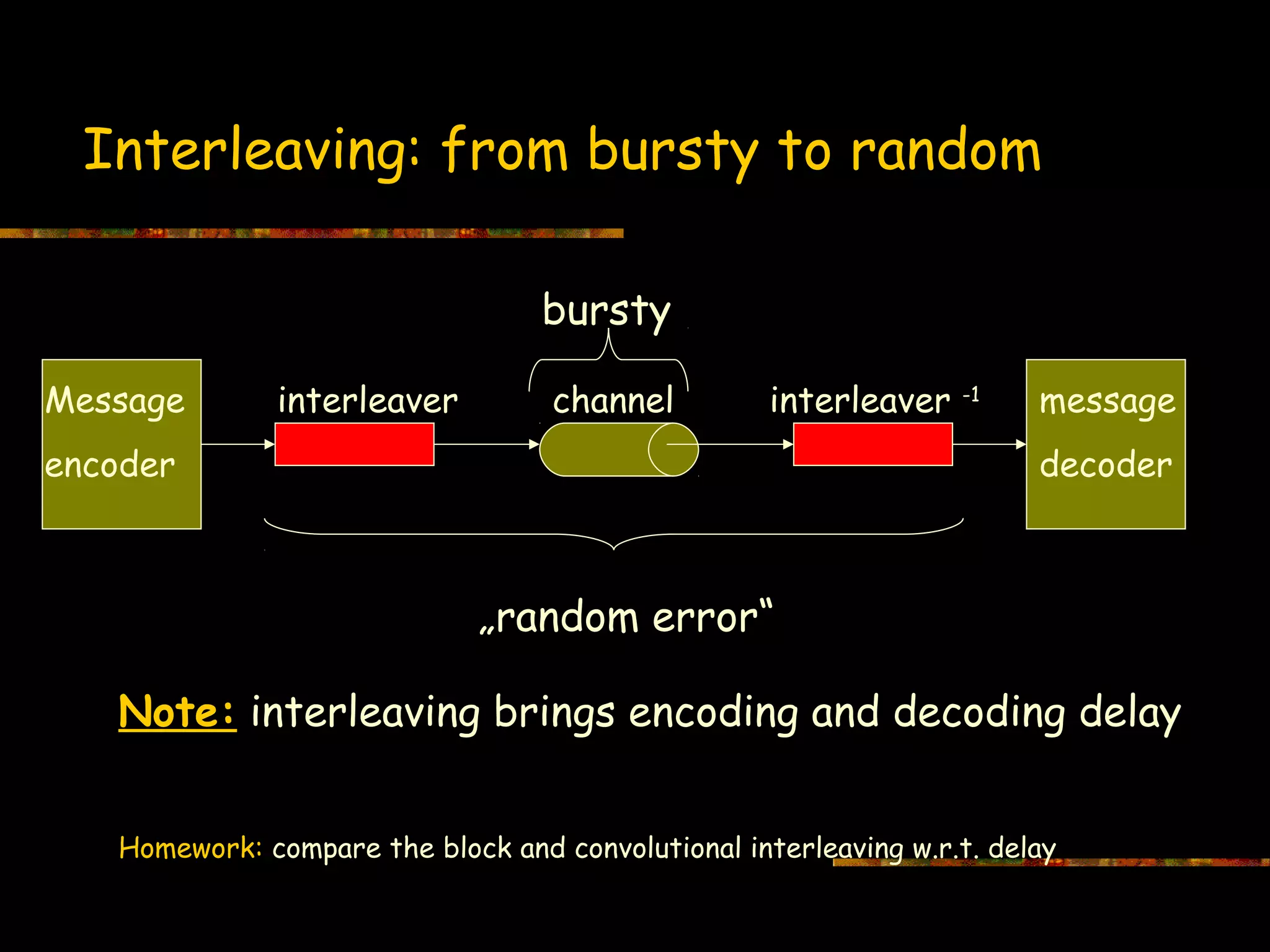
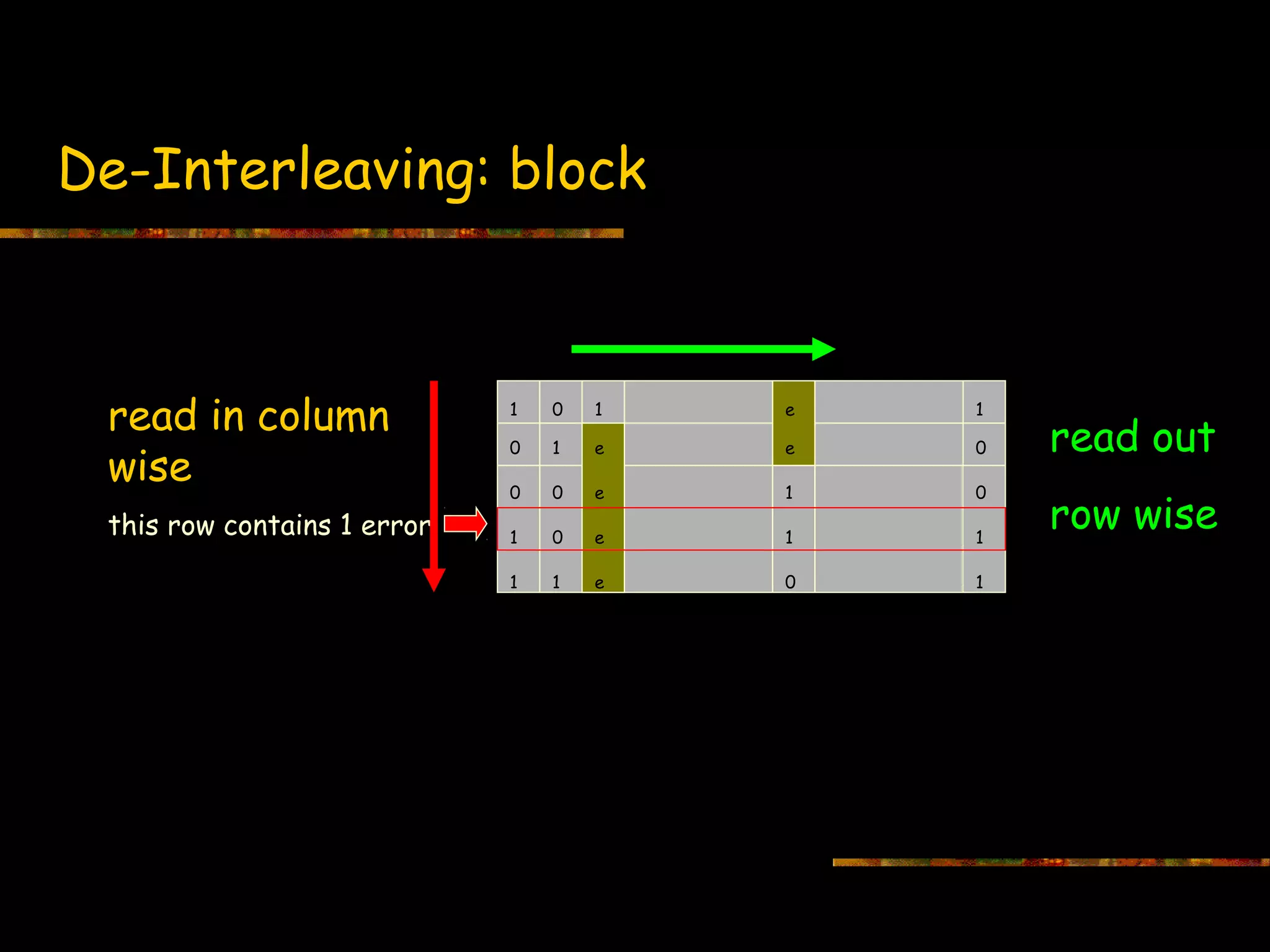
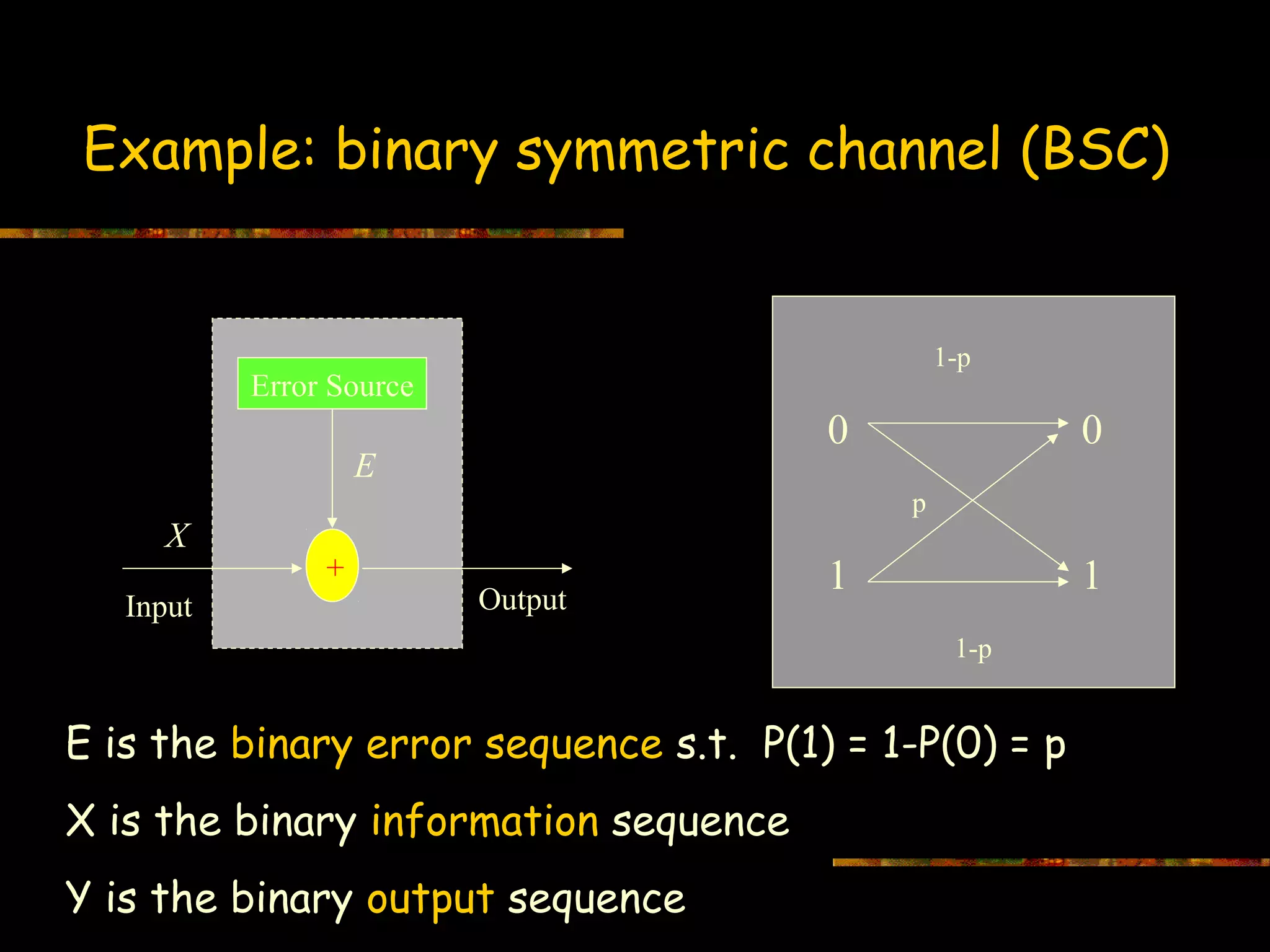
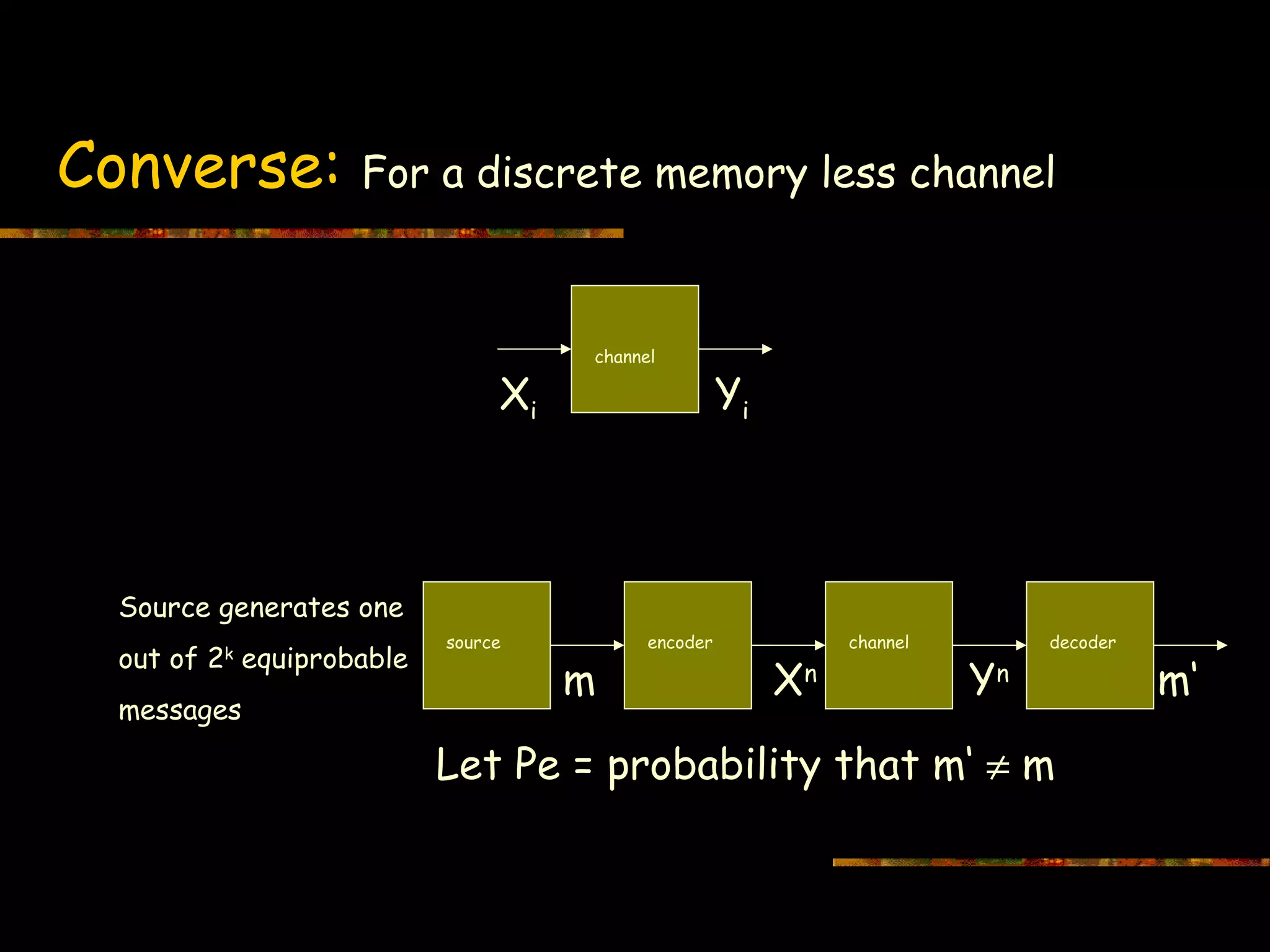
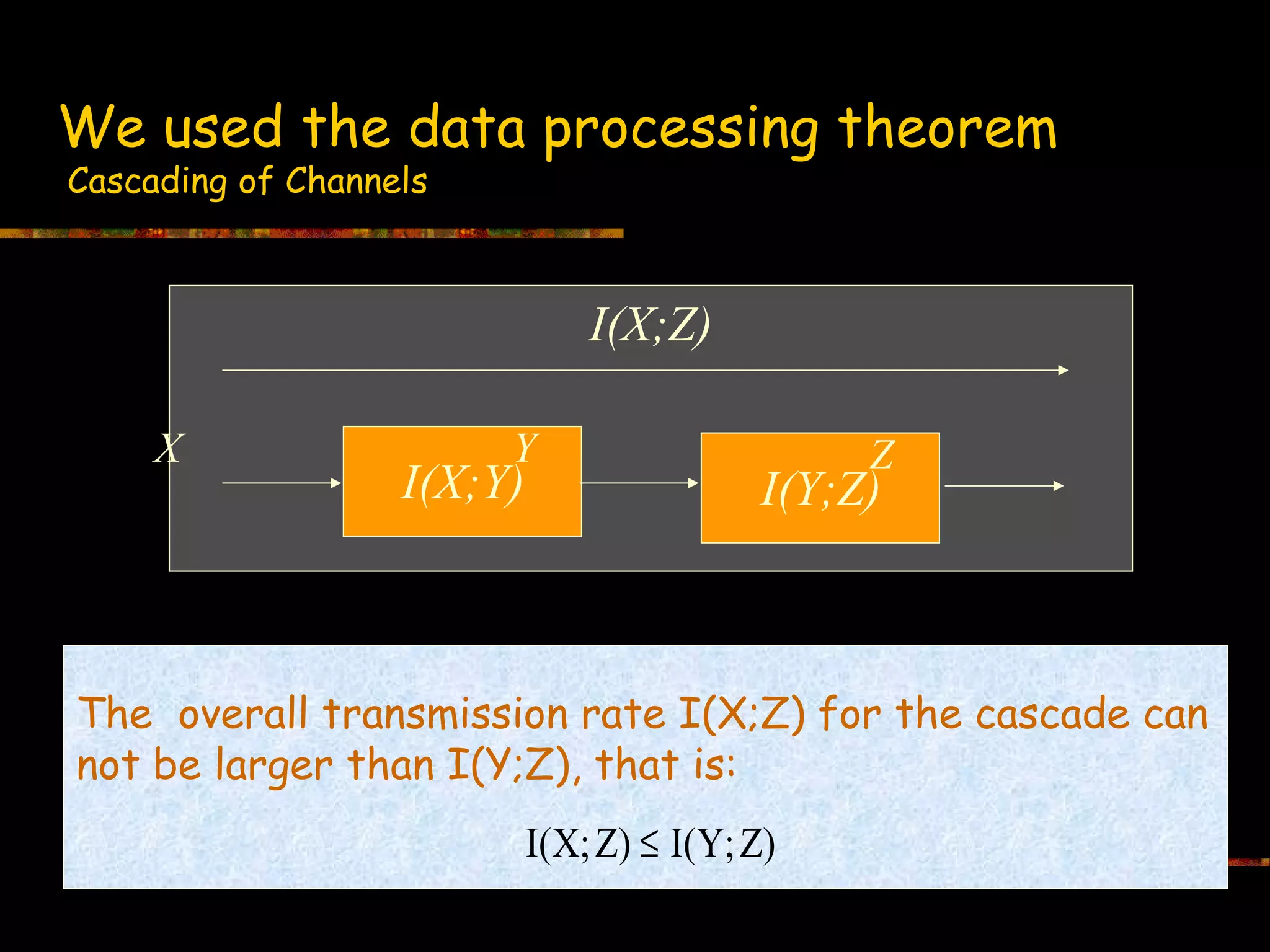
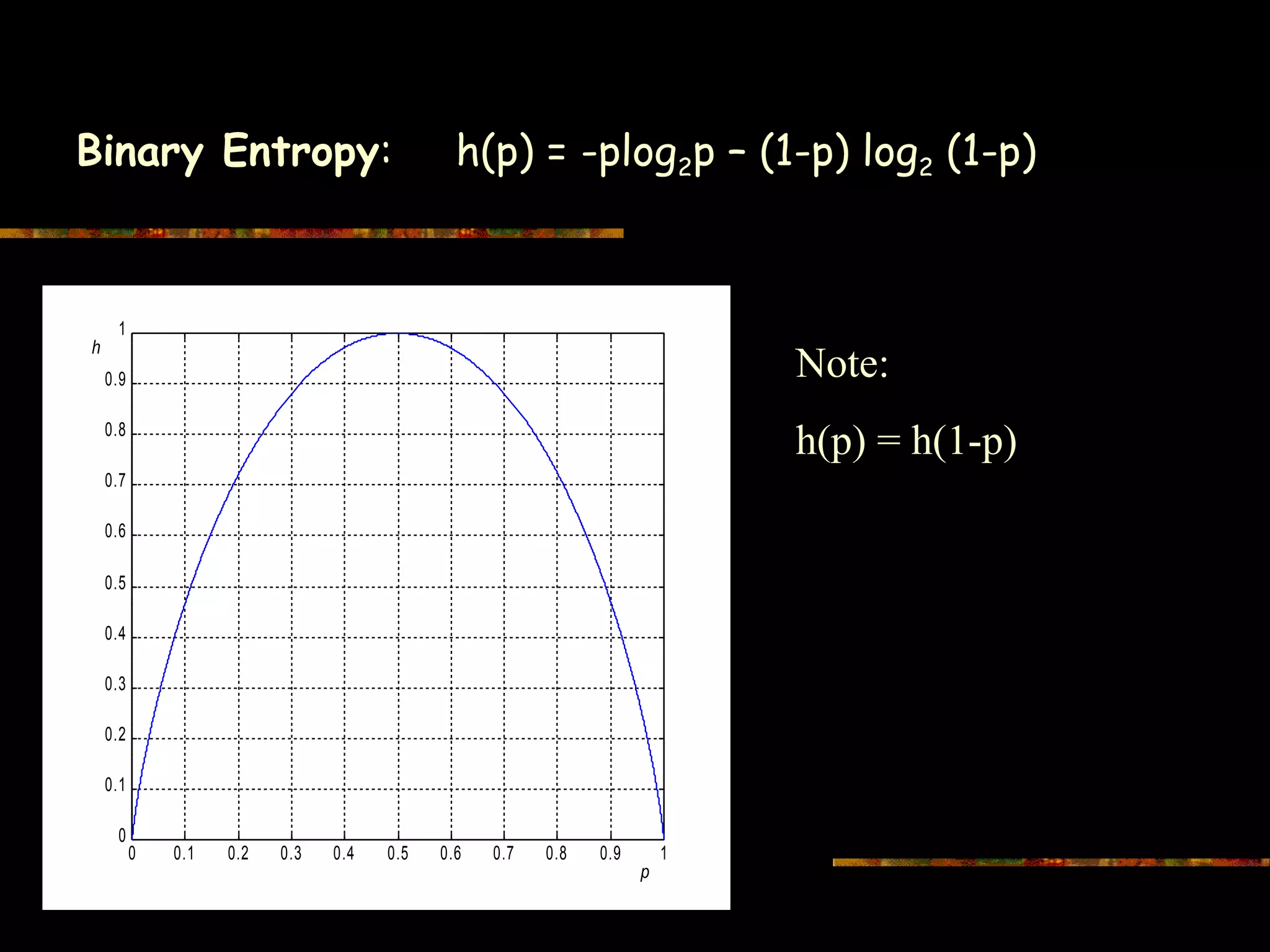
This document introduces information theory and channel capacity models. It discusses several channel models including the binary symmetric channel (BSC), binary erasure channel, and additive white Gaussian noise channel. It explains how channel capacity is defined as the maximum rate of error-free transmission and derives the capacity for some basic channels. The document also covers channel coding techniques like interleaving that can improve performance by converting burst errors into random errors.

1. Introduction to Information
theory
channel capacity and models
A.J. Han Vinck
University of Essen
May 2011

2. This lecture
 Some models
 Channel capacity
 Shannon channel coding theorem
 converse

3. some channel models
Input X P(y|x) output Y
transition probabilities
memoryless:
- output at time i depends only on input at time i
- input and output alphabet finite

4. Example: binary symmetric channel (BSC)
1-p
Error Source
0 0
E
p
X Y = X ⊕E
+ 1 1
Input Output
1-p
E is the binary error sequence s.t. P(1) = 1-P(0) = p
X is the binary information sequence
Y is the binary output sequence

5. from AWGN
to BSC
p
Homework: calculate the capacity as a function of A and σ2

6. Other models
1-e
0 0 (light on) 0 0
e
X p Y
1-p 1 (light off)
1
e
1 1
P(X=0) = P0
P(X=0) = P0
Z-channel (optical) Erasure channel
(MAC)

7. Erasure with errors
1-p-e
0 0
e
p
p e
1 1
1-p-e

8. burst error model (Gilbert-Elliot)
Random error channel; outputs independent
Error Source P(0) = 1- P(1);
Burst error channel; outputs dependent
P(0 | state = bad ) = P(1|state = bad ) = 1/2;
Error Source
P(0 | state = good ) = 1 - P(1|state = good ) = 0.999
State info: good or bad transition probability
Pgb
Pgg good bad Pbb
Pbg

9. channel capacity:
I(X;Y) = H(X) - H(X|Y) = H(Y) – H(Y|X) (Shannon 1948)
X Y
H(X) channel H(X|Y)
max I(X; Y) = capacity
P( x )
notes:
capacity depends on input probabilities
because the transition probabilites are fixed

10. Practical communication system design
Code book
Code receive
message word in
estimate
2k channel decoder
Code book
with errors
n
There are 2k code words of length n
k is the number of information bits transmitted in n channel uses

11. Channel capacity
Definition:
The rate R of a code is the ratio k/n, where
k is the number of information bits transmitted in n channel uses
Shannon showed that: :
for R ≤ C
encoding methods exist
with decoding error probability 0

12. Encoding and decoding according to Shannon
Code: 2k binary codewords where p(0) = P(1) = ½
Channel errors: P(0 →1) = P(1 → 0) = p
i.e. # error sequences ≈ 2nh(p)
Decoder: search around received sequence for codeword
with ≈ np differences
space of 2n binary sequences

13. decoding error probability
1. For t errors: |t/n-p|> Є
→ 0 for n → ∞
(law of large numbers)
2. > 1 code word in region
(codewords random)
2 nh ( p)
P(> 1) ≈ (2 k − 1)
2n
→ 2 − n (1− h ( p)− R ) = 2 − n (C BSC − R ) → 0
k
for R = < 1 − h (p)
n
and n → ∞

14. channel capacity: the BSC
1-p I(X;Y) = H(Y) – H(Y|X)
0 0 the maximum of H(Y) = 1
X p Y since Y is binary
1 1 H(Y|X) = h(p)
1-p = P(X=0)h(p) + P(X=1)h(p)
Conclusion: the capacity for the BSC CBSC = 1- h(p)
Homework: draw CBSC , what happens for p > ½

15. channel capacity: the BSC
Explain the behaviour!
1.0
Channel capacity
0.5 1.0
Bit error p

16. channel capacity: the Z-channel
Application in optical communications
0 0 (light on) H(Y) = h(P0 +p(1- P0 ) )
X p Y
H(Y|X) = (1 - P0 ) h(p)
1-p 1 (light off)
1
For capacity,
P(X=0) = P0 maximize I(X;Y) over P0

17. channel capacity: the erasure channel
Application: cdma detection
1-e
0 0 I(X;Y) = H(X) – H(X|Y)
e
H(X) = h(P0 )
X Y
H(X|Y) = e h(P0)
e
1 1
Thus Cerasure = 1 – e
P(X=0) = P0
(check!, draw and compare with BSC and Z)

18. Erasure with errors: calculate the capacity!
1-p-e
0 0
e
p
p e
1 1
1-p-e

19. 0 0
1/3
example 1 1
1/3
2 2
 Consider the following example
 For P(0) = P(2) = p, P(1) = 1-2p
H(Y) = h(1/3 – 2p/3) + (2/3 + 2p/3); H(Y|X) = (1-2p)log23
Q: maximize H(Y) – H(Y|X) as a function of p
Q: is this the capacity?
hint use the following: log2x = lnx / ln 2; d lnx / dx = 1/x

20. channel models: general diagram
P1|1 y1
x1
P2|1 Input alphabet X = {x1, x2, …, xn}
P1|2
x2 y2
P2|2 Output alphabet Y = {y1, y2, …, ym}
: Pj|i = PY|X(yj|xi)
:
:
:
: In general:
:
xn calculating capacity needs more
Pm|n
theory
ym
The statistical behavior of the channel is completely defined by
the channel transition probabilities Pj|i = PY|X(yj|xi)

21. * clue:
I(X;Y)
is convex ∩ in the input probabilities
i.e. finding a maximum is simple

22. Channel capacity: converse
For R > C the decoding error probability > 0
Pe
k/n
C

23. Converse: For a discrete memory less channel
channel
Xi Yi
n n n n
I ( X ; Y ) = H (Y ) − ∑ H (Yi | X i ) ≤ ∑ H (Yi ) − ∑ H (Yi | X i ) = ∑ I ( X i ; Yi ) ≤ nC
n n n
i =1 i =1 i =1 i =1
Source generates one
source encoder channel decoder
out of 2k equiprobable
m Xn Yn m‘
messages
Let Pe = probability that m‘ ≠ m

24. converse R := k/n
k = H(M) = I(M;Yn)+H(M|Yn)
1 – C n/k - 1/k ≤ Pe
≤ I(Xn;Yn) + 1 + k Pe
≤ nC + 1 + k Pe
Pe ≥ 1 – C/R - 1/nR
Hence: for large n, and R > C,
the probability of error Pe > 0

25. We used the data processing theorem
Cascading of Channels
I(X;Z)
X Y Z
I(X;Y) I(Y;Z)
The overall transmission rate I(X;Z) for the cascade can
not be larger than I(Y;Z), that is:
I(X; Z) ≤ I(Y; Z)

26. Appendix:
Assume:
binary sequence P(0) = 1 – P(1) = 1-p
t is the # of 1‘s in the sequence
Then n → ∞ , ε > 0
Weak law of large numbers
Probability ( |t/n –p| > ε ) → 0
i.e. we expect with high probability pn 1‘s

27. Appendix:
Consequence:
1. n(p- ε) < t < n(p + ε) with high probability
n ( p + ε) n n
2. ∑   ≈ 2nε  ≈ 2nε2 nh ( p)
t  pn 
n ( p −ε)    
1 log 2nε  n 
lim n 2   → h ( p) h (p) = − p log 2 p − (1 − p) log 2 (1 − p)
3. n→ ∞
 pn 
 
Homework: prove the approximation using ln N! ~ N lnN for N large.
N −N
Or use the Stirling approximation: N ! → 2π N N e

28. Binary Entropy: h(p) = -plog2p – (1-p) log2 (1-p)
1
h
0.9 Note:
0.8
h(p) = h(1-p)
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
p

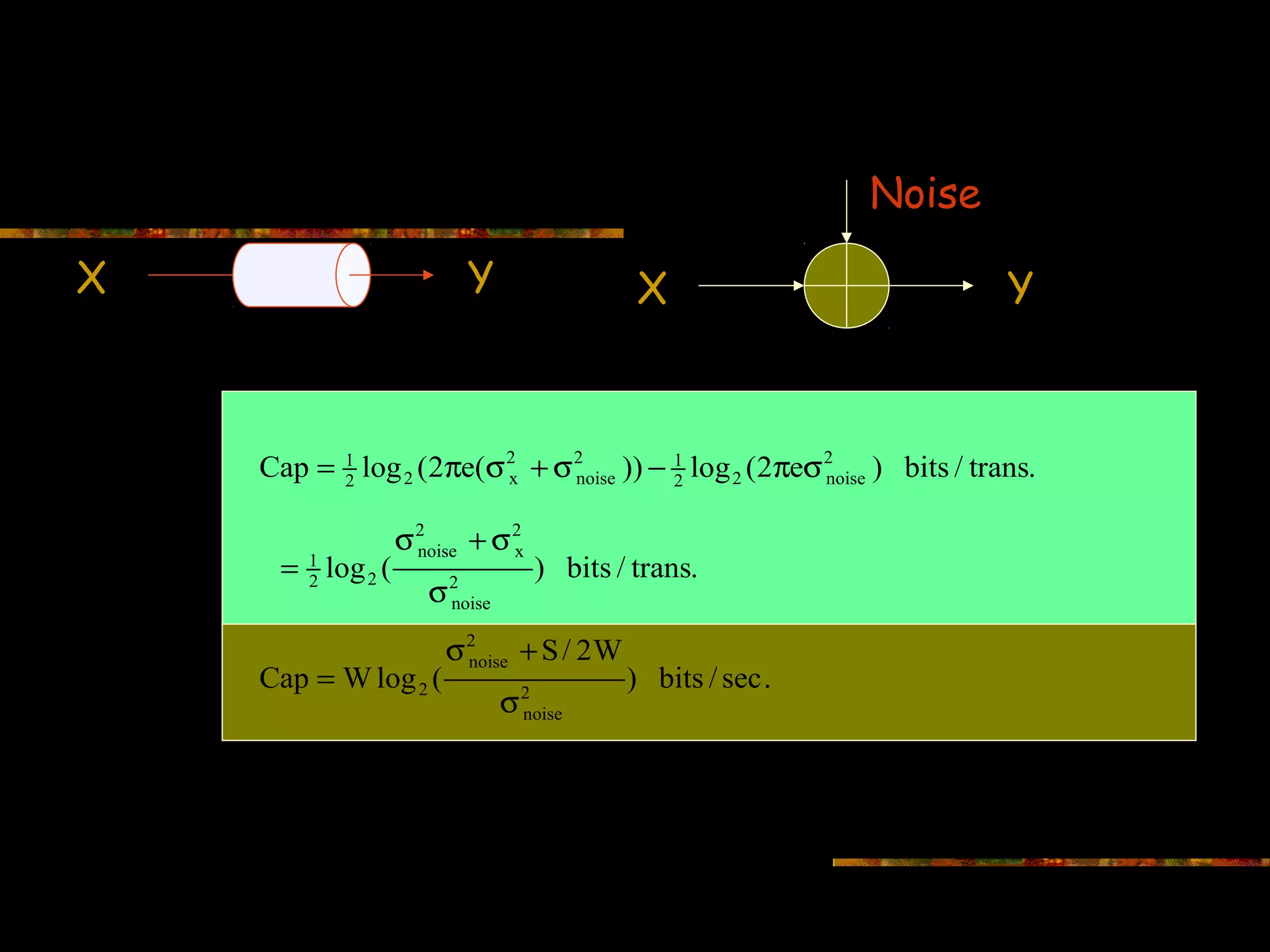
29. Capacity for Additive White Gaussian Noise
Noise
Input X Output Y
Cap := sup [H(Y) − H( Noise)]
p( x )
x 2 ≤S / 2 W W is (single sided) bandwidth
Input X is Gaussian with power spectral density (psd) ≤S/2W;
Noise is Gaussian with psd = σ2noise
Output Y is Gaussian with psd = σy2 = S/2W + σ2noise
For Gaussian Channels: σy2 = σx2 +σnoise2

30. Noise
X Y X Y
Cap = 1 log 2 (2πe(σ 2 + σ 2 )) − 1 log 2 (2πeσ 2 ) bits / trans.
2 x noise 2 noise
σ2 + σ2
noise x
= 1 log 2 (
2
) bits / trans.
σ 2
noise
σ2 + S / 2W
noise
Cap = W log 2 ( ) bits / sec .
σ2
noise
1 −z2 / 2 σ2
p(z) = e z
; H(Z) = 2 log2 (2πeσ2 ) bits
1
z
2πσ2
z

31. Middleton type of burst channel model
0 0
1 1
Transition
probability P(0)
channel 1
channel 2
Select channel k …
with probability channel k has
Q(k) transition
probability p(k)

32. Fritzman model:
multiple states G and only one state B
Closer to an actual real-world channel
1-p
G1 … Gn B
Error probability 0 Error probability h

33. Interleaving: from bursty to random
bursty
Message interleaver channel interleaver -1
message
encoder decoder
„random error“
Note: interleaving brings encoding and decoding delay
Homework: compare the block and convolutional interleaving w.r.t. delay

34. Interleaving: block
Channel models are difficult to derive:
- burst definition ?
- random and burst errors ?
for practical reasons: convert burst into random error
read in row wise 1 0 1 0 1
transmit
0 1 0 0 0
0 0 0 1 0 column wise
1 0 0 1 1
1 1 0 0 1

35. De-Interleaving: block
read in column 1 0 1 e 1
read out
wise
0 1 e e 0
0 0 e 1 0
this row contains 1 error 1 0 e 1 1
row wise
1 1 e 0 1

36. Interleaving: convolutional
input sequence 0
input sequence 1 delay of b elements
•••
input sequence m-1 delay of (m-1)b elements
in
Example: b = 5, m = 3
out