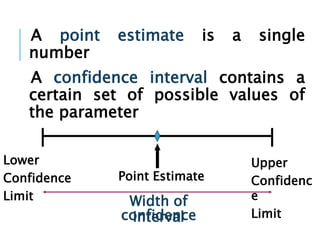
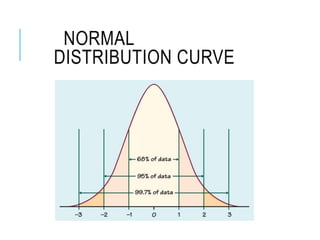
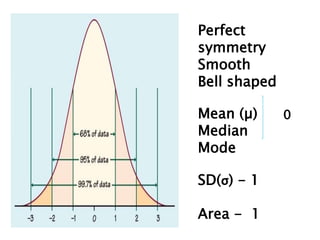
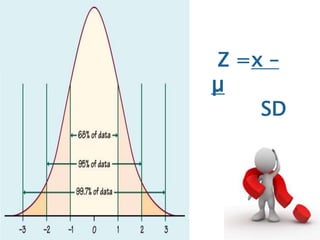
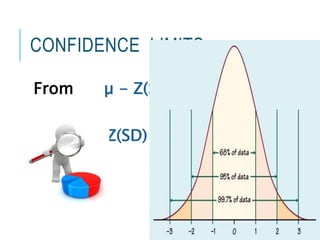
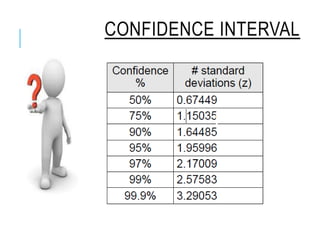
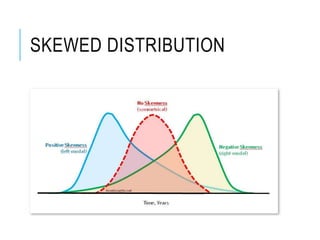
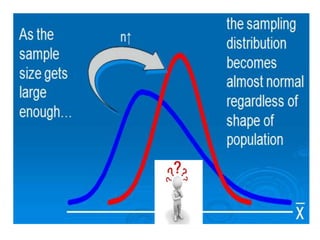
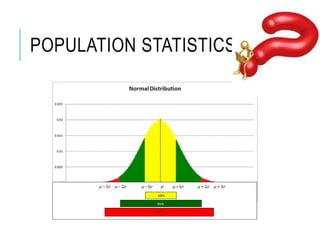
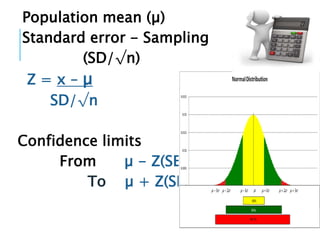
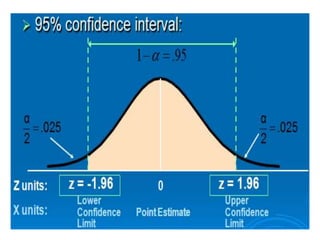
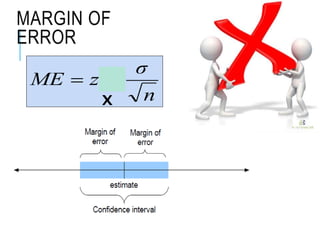
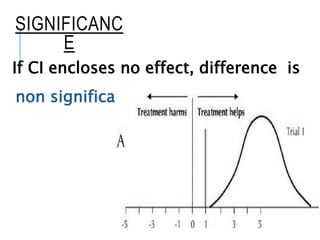
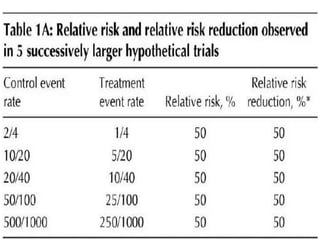
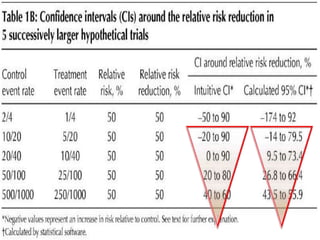
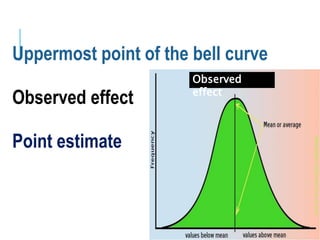
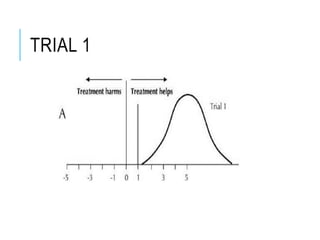
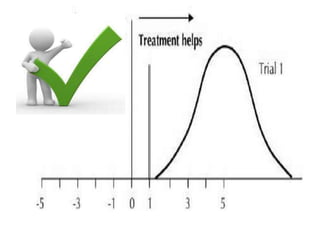
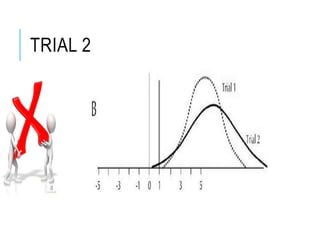
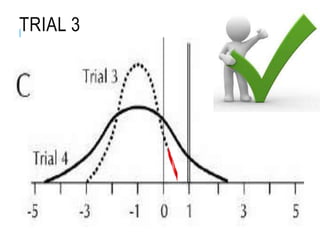
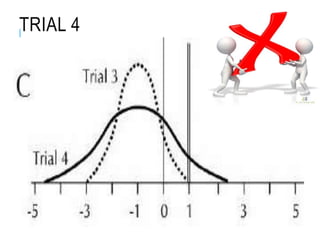
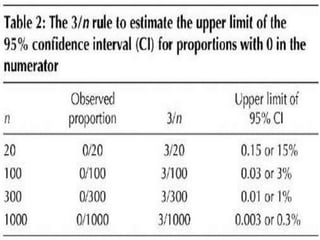
This document discusses confidence intervals, which provide a range of values that is likely to include an unknown population parameter based on a sample statistic. It defines key concepts like confidence level, confidence limits, and factors that determine how to set the confidence interval like sample size, population variability, and precision of values. It explains how larger sample sizes and more precise measurements result in narrower confidence intervals. Applications to clinical trials are discussed, showing how sample size impacts the ability to make definitive recommendations based on trial results.

1. CONFIDENCE
INTERVAL
Dr.RENJ
U

2. OVERVIEW
INTRODUCTION
CONFIDENCE INTERVAL
CONFIDENCE LEVEL
CONFIDENCE LIMITS
HOW TO SET?
FACTORS – SET
SIGNIFICANCE
APPLICATIONS

3. INTRODUCTIO
N
Statistical parameter
Descriptive statistics :
Describe what is there in our data
Inferential statistics :
Make inferences from our data to
more general conditions

4. Inferential statistics
Data taken from a sample is
used to estimate a population
parameter
Hypothesis testing (P-values)
Point estimation (Confidence
intervals)

5. POINT ESTIMATE
Estimate obtained from a sample
Inference about the population
Point estimate is only as good as the
sample it represents
Random samples from the
population - Point estimates likely to
vary

6. ISSUE ???
Variation in sample statistics

7. SOLUTION
Estimating a population
parameter with a confidence
interval

8. CONFIDENCE INTERVAL
A range of values so constructed
that there is a specified probability
of including the true value of a
parameter within it

9. CONFIDENCE LEVEL
Probability of including the true
value of a parameter within a
confidence interval
Percentage

10. CONFIDENCE LIMITS
Two extreme measurements
within which an observation
lies
End points of the confidence
interval
Larger confidence – Wider

11. A point estimate is a single
number
A confidence interval contains a
certain set of possible values of
the parameter
Point Estimate
Lower
Confidence
Limit
Upper
Confidenc
e
Limit
Width of
confidenceinterval

12. HOW TO
SET

13. CONCEPTS
NORMAL DISTRIBUTION CURVE
MEAN ( µ )
STANDARD DEVIATION (SD)
RELATIVE DEVIATE (Z)

14. NORMAL
DISTRIBUTION CURVE

15. Perfect
symmetry
Smooth
Bell shaped
Mean (µ)
Median
Mode
SD(σ) - 1
Area - 1
0

16. RELATIVE DEVIATE (Z)
Distance of a value (X) from mean
value (µ) in units of standard
deviation (SD)
Standard normal variate

17. Z =x –
µ
SD

18. CONFIDENCE LIMITS
From µ - Z(SD)
To µ + Z(SD)

19. CONFIDENCE INTERVAL

20. FACTORS – TO SET CI
Size of sample
Variability of population
Precision of values

21. SAMPLE SIZE
Central Limit Theorem
“Irrespective of the shape of the
underlying distribution, sample mean &
proportions will approximate normal
distributions if the sample size is
sufficiently large”
Large sample – Narrow CI

22. SKEWED DISTRIBUTION

24. VARIABILITY OF
POPULATION

25. POPULATION
STATISTICS
Repeated samples
Different means
Standard normal curve
Bell shape
Smooth
Symmetrical

26. POPULATION STATISTICS

27. Population mean (µ)
Standard error - Sampling
(SD/√n)
Z = x – µ
SD/√n
Confidence limits
From µ - Z(SE)
To µ + Z(SE)

28. 95%
95% sample means are
within 2 SD of population
mean

29. PRECISION OF VALUES
Greater precision

Narrow confidence interval
Larger sample size

30. PRECISION OF
VALUES

31. SIGNIFICANCE

32. 95%
Significance
Observed value
within 2 SD of true
value

33. CONFIDENCE INTERVAL AND
Α ERROR
Type I error
Two groups
Significant difference is detected
Actual – No difference exists
False Positive

35. Confidence level is usually set at
95%
(1– ) = 0.95

36. MARGIN OF
ERROR
n
σ
zME α/ 2
x

37. Margin of error
Reduce the SD (σ↓)
Increase the sample size (n↑)
Narrow confidence level (1 – ) ↓

38. P VALUE
95% CI corresponds to
hypothesis testing with P <0.05

39. SIGNIFICANC
E
If CI encloses no effect, difference is
non significant

40. P value – Statistical significance
Confidence Interval – Clinical
significance

41. APPLICATIONS
CLINICAL TRIALS

42. Margin of error
Increase the sample size
Reduce confidence level
Dynamic relation
Confidence intervals and
sample size

43. EXAMPLE
Series of 5 trials
Equal duration
Different sample sizes
To determine whether a novel
hypolipidaemic agent is better than
placebo in preventing stroke

44. Smallest trial  8 patients
Largest trial 2000 patients
½ of the patients in each trial – New drug
All trials - Relative risk reduction by 50%

46. QUESTION
S
In each individual trial, how
confident can we be regarding
the relative risk reduction
Which trials would lead you to
recommend the treatment
unequivocally to your patients

47. MORE CONFIDENT - LARGER
TRIALS
CI - Range within
which the true effect
of test drug might
plausibly lie in the
given trial data

49. Greater precision
Narrow confidence intervals
Large sample size

50. THERAPEUTIC
DECISIONS
Recommend for or against
therapy ?

51. Minimally Important Treatment
Effect
Smallest amount of benefit that
would justify therapy
Points

52. Uppermost point of the bell curve
Observed effect
Point estimate
Observed
effect

53. Tails of the bell curve
Boundaries of the 95% confidence
interval
Observed
effect

54. TRIAL 1

56. TRIAL 2

57. CI overlaps the smallest
treatment benefit
Not Definitive
Need narrower Confidence
interval
Larger sample size

58. TRIAL 3

59. TRIAL 4

60. CI overlaps the smallest
treatment benefit
Not Definitive
Need narrower Confidence
interval
Larger sample size

61. CONFIDENCE INTERVALS
FOR
EXTREME PROPORTIONS
Proportions with numerator – 0
Proportions approaching - 1
Proportions with numerators very
close to the corresponding
denominators

62. NUMERATOR - 0
Rule of 3
Proportion – 0/n
Confidence level – 95%
Upper boundary – 3/n

63. EXAMPL
E
20 people – Surgery
None had serious complications
Proportion 0/20
3/n – 3/20
15%

65. PROPORTIONS APPROACHING - 1
Translate 100% into its complement

66. EXAMPL
E
Study on a diagnostic test
100% sensitivity when the test is
performed for 20 patients who have
the disease.
Test identified all 20 with the
disease as positive – 100%
No falsely negatives – 0%

67. 95% Confidence level
Proportion of false negatives - 0 /20
3/n rule
Upper boundary - 15% (3 /20 )
Sensitivity
Lower boundary
Subtract this from 100%
100 – 15 = 85%

68. NUMERATORS VERY CLOSE TO
THE DENOMINATORS
Rule
Numerator X
1 5
2 7
3 9
4 10

69. 95% Confidence level
Upper boundary –

70. CONCLUSION
Confidence interval
Confidence level
Confidence limits
95%
Observed value within 2 SD
Population statistics

71. THANK YOU