This document discusses statistical estimation and provides information about objectives, outline, statistical inference, estimation types (point and interval), confidence intervals, and sample size calculation. The key points are:
- The objectives are to describe statistical inference, differentiate between point and interval estimation, compute confidence intervals, and describe sample size calculation methods.
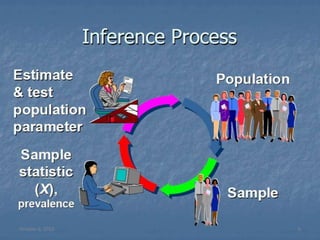
- Point estimation provides a single value to estimate a population parameter, while interval estimation provides a range of values that the population parameter is likely to fall within.
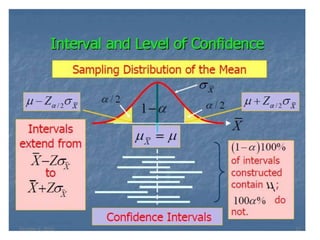
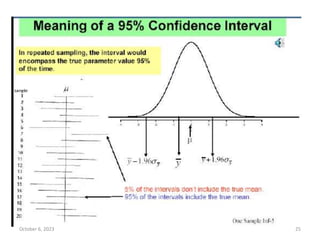
- Confidence intervals account for sample to sample variation and give a measure of precision for estimates. Common confidence levels are 90%, 95%, and 99%.


















![proportion
estimating
for
n
P
P
z
p
n
P
P
z
p
e
s
by
estimated
be
can
it
unknown
is
if
mean
estimating
for
n
z
x
n
z
x
]
/
)
1
(
.
,
/
)
1
(
.
[
.
,
]
.
,
.
[
2
2
2
2
October 6, 2023 20
A (1-α) 100% confidence interval for unknown population mean
and population proportion is given as follows;](https://image.slidesharecdn.com/estimation-231006163158-3fd219ca/85/estimation-pptx-20-320.jpg)