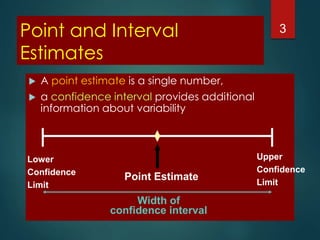
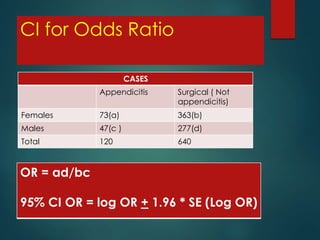
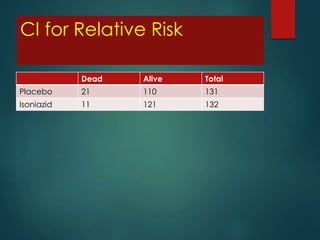
This document discusses confidence intervals and probability. It defines confidence intervals as a range of values that provide more information than a point estimate by taking into account variability between samples. The document provides examples of how to calculate 95% confidence intervals for a proportion, mean, odds ratio, and relative risk using sample data and the appropriate formulas. It explains that confidence intervals convey the level of uncertainty associated with point estimates and allow estimation of how close a sample statistic is to the unknown population parameter.

1. Confidence Interval
&
Probability
Dr Zahid Khan
SENIOR LECTURER KING FAISAL UNIVERSITY

2. 2
Confidence Intervals

How much uncertainty is associated with
a point estimate of a population
parameter?

An interval estimate provides more
information about a population
characteristic than does a point estimate

Such interval estimates are called
confidence intervals

3. Point and Interval
Estimates


3
A point estimate is a single number,
a confidence interval provides additional
information about variability
Lower
Confidence
Limit
Point Estimate
Width of
confidence interval
Upper
Confidence
Limit

4. 4
Point Estimates
We can estimate a
Population Parameter …
with a Sample
Statistic
(a Point Estimate)
Mean
μ
x
Proportion
p
p

5. Confidence Interval
Estimate

An interval gives a range of values:
 Takes
into consideration variation in
sample statistics from sample to
sample
 Based
on observation from 1 sample
 Gives
information about closeness to
unknown population parameters
 Stated
in terms of level of confidence
Never
100% sure

6. Estimation Process
Random Sample
Population
(mean, μ, is
unknown)
Sample
Mean
x = 50
I am 95%
confident that
μ is between
40 & 60.

7. Confidence interval
endpoints

Upper and lower confidence limits for the
population proportion are calculated with the
formula
p  z/2

p(1p)
n
where

z is the standard normal value for the level of confidence desired

p is the sample proportion

n is the sample size

8. Example

A random sample of 100 people shows that 25 are left-handed.

Form a 95% confidence interval for the true proportion of left-handers

9. Example

A random sample of 100 people shows that 25 are lefthanded. Form a 95% confidence interval for the true
proportion of left-handers.


.25
1. p 25/100
(1
p 

.0433
2. S p  )/n .25(.75)/n
p
3.
.251.96

(.0433)
0.16510.3349
.....

10. Interpretation

We are 95% confident that the true percentage of lefthanders in the population is between
16.51% and 33.49%.

Although this range may or may not contain the true
proportion, 95% of intervals formed from samples of size
100 in this manner will contain the true proportion.

11. Changing the sample size

Increases in the sample size reduce the width of the confidence
interval.
Example:

If the sample size in the above example is doubled to 200,
and if 50 are left-handed in the sample, then the interval
is still centered at .25, but the width shrinks to
.19 …… .31

12. 95% CI for Mean
 μ+
1.96 * SE


SE=
SD²/n


SE difference =
SD²/n1 + SD²/n2

13. CI for Odds Ratio
CASES
Appendicitis
Surgical ( Not
appendicitis)
Females
73(a)
363(b)
Males
47(c )
277(d)
Total
120
640
OR = ad/bc
95% CI OR = log OR + 1.96 * SE (Log OR)

14. CI for OR

SE ( loge OR) = 1/a + 1/b + 1/c + 1/d

= 1/73 + 1/363 + 1/47 + 1/277 = 0.203

Loge of the Odds Ratio is 0.170.

95% CI = 0.170 – 1.96 * 0.203 to 0.170 * 1.96 * 0.203

Loge OR = -0.228 to 0.578

Now by taking antilog ex we get 0.80 to 1.77 for 0.228 and
0.578 respectively.

15. CI for Relative Risk
Dead
Alive
Total
Placebo
21
110
131
Isoniazid
11
121
132

16. CI for Relative Risk

SE ( LogRR) =
1/a – 1/a+b + 1/c – 1/c+d

SE (LogRR) = 1/21-1/131 + 1/11 – 1/132 = 0.351

RR = a/ a+b / c/ c+d = 0.52

LogRR = Log 0.52 = - 0.654

95% CI = -0.654 -1.96 * 0.351 , -0.654 +1.96 * 0.351

= -1.42, 0.040 so by taking anti log we have

95% CI = 0.242, 1.04