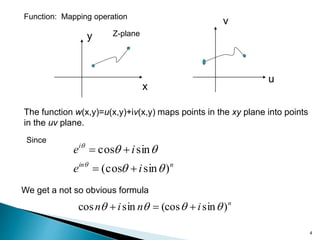
1) Complex numbers can be represented in Cartesian (x + iy) or polar (r(cosθ + i sinθ)) form, with conversions between the two. 2) The derivative of a complex function f(z) is defined if the Cauchy-Riemann equations are satisfied. 3) A function is analytic if it is differentiable and its partial derivatives are continuous, implying the Cauchy-Riemann equations always hold. Analytic functions have properties like equality of second partial derivatives.

1. We here go through the complex algebra briefly.
A complex number z = (x,y) = x + iy, Where
We will see that the ordering of two real numbers (x,y) is significant,
i.e. in general x + iy  y + ix
X: the real part, labeled by Re(z); y: the imaginary part, labeled by Im(z)
Three frequently used representations:
(1) Cartesian representation: x+iy
(2) polar representation, we may write
z=r(cos  + i sin) or
r – the modulus or magnitude of z
 - the argument or phase of z
1


i
1

i
e
r
z 


2. 2
r – the modulus or magnitude of z
 - the argument or phase of z
The relation between Cartesian
and polar representation:
The choice of polar representation or Cartesian representation
is a
matter of convenience. Addition and subtraction of complex
variables
are easier in the Cartesian representation. Multiplication,
division, powers, roots are easier to handle in polar form,
 
 
1/ 2
2 2
1
tan /
r z x y
y x
 
  

 
2
1
2
1
2
1

 
 i
e
r
r
z
z
   
2
1
2
1
2
1 /
/ 
 
 i
e
r
r
z
z

in
n
n
e
r
z 
)
(
)
(
)
(
)
(
2
2
2
1
2
1
2
1
2
1
2
1
2
1
2
1
y
x
y
x
i
y
y
x
x
z
z
y
y
i
x
x
z
z










3. From z, complex functions f(z) may be constructed.
They can be written
f(z) = u(x,y) + iv(x,y)
in which v and u are real functions.
For example if , we have
The relationship between z and f(z) is best pictured
as a mapping operation, we address it in detail
later.
)
arg(
)
arg(
)
arg( 2
1
2
1 z
z
z
z 

3
2
1
2
1 z
z
z
z 
    xy
i
y
x
z
f 2
2
2



Using the polar form,
2
)
( z
z
f 

4. 4
Function: Mapping operation
x
y Z-plane
u
v
The function w(x,y)=u(x,y)+iv(x,y) maps points in the xy plane into points
in the uv plane.
n
in
i
i
e
i
e
)
sin
(cos
sin
cos










We get a not so obvious formula
Since
n
i
n
i
n )
sin
(cos
sin
cos 


 



5. Complex Conjugation: replacing i by –i, which is denoted by (*),
We then have
Hence
Note:
ln z is a multi-valued function. To avoid ambiguity, we usually
set n=0
and limit the phase to an interval of length of 2. The value of
lnz with
n=0 is called the principal value of lnz.
5
iy
x
z 

*
2
2
2
*
r
y
x
zz 


  2
1
*
zz
z  Special features: single-valued function of a
real variable ---- multi-valued function

i
re
z   

 n
i
re 2



 i
r
ln
z
ln  

 n
i
r
z 2
ln
ln 



6. 6
Another possibility




even
and
1
|
cos
|
|,
sin
|
possibly
however,
x;
real
a
for
1
|
cos
|
|,
sin
|
z
z
x
x
Question:
y
x
y
x
y
x
i
y
x
iy
x
y
x
i
y
x
iy
x
i
e
e iz
iz
2
2
2
2
2
2
iz
iz
sinh
cos
|
cosz
|
sinh
sin
|
sinz
|
(b)
sinh
sin
cosh
cos
)
cos(
sinh
cos
cosh
sin
)
sin(
(a)
show
to
2
e
sinz
;
2
e
cosz
:
identities
the
Using

















7. Having established complex functions, we now proceed to
differentiate them. The derivative of f(z), like that of a real
function, is
defined by
provided that the limit is independent of the particular
approach to the
point z. For real variable, we require that
Now, with z (or zo) some point in a plane, our requirement that
the
limit be independent of the direction of approach is very
restrictive.
Consider
7
       
z
f
dz
df
z
z
f
z
z
f
z
z
f
z
z







 




 0
0
lim
lim
     
o
x
x
x
x
x
f
x
f
x
f
o
o









lim
lim
y
i
x
z 

 

v
i
u
f 

 

,
y
i
x
v
i
u
z
f










8. Let us take limit by the two different approaches as in the
figure. First,
with y = 0, we let x0,
Assuming the partial derivatives exist. For a second approach,
we set
x = 0 and then let y 0. This leads to
If we have a derivative, the above two results must be identical.
So,
8









 x
v
i
x
u
z
f
x
z 






 0
0
lim
lim
x
v
i
x
u






y
v
y
u
i
z
f
z 






 

 0
lim
y
v
x
u





,
x
v
y
u







9. These are the famous Cauchy-Riemann conditions. These
Cauchy-
Riemann conditions are necessary for the existence of a
derivative, that
is, if exists, the C-R conditions must hold.
Conversely, if the C-R conditions are satisfied and the partial
derivatives of u(x,y) and v(x,y) are continuous, exists. (see
the proof
in the text book).
9
 
x
f
 
z
f

10. 10
Analytic functions
If f(z) is differentiable at and in some small region around ,
we say that f(z) is analytic at
Differentiable: Cauthy-Riemann conditions are satisfied
the partial derivatives of u and v are continuous
Analytic function:
Property 1:
Property 2: established a relation between u and v
0
2
2



 v
u
Example:
x
e
y
x
v
b
xy
x
y
x
u
a
y
x
iv
y
x
u
z
w
y
sin
)
,
(
)
(
3
)
,
(
)
(
if
)
,
(
)
,
(
)
(
functions
analytic
the
Find
2
3






0
z
z 
0
z
z 
0
z