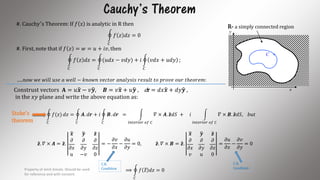
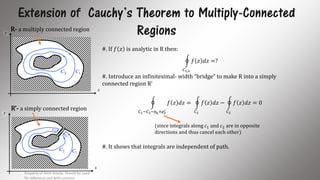
The document discusses line integrals in the complex plane. It defines line integrals, shows how complex line integrals are equivalent to two real line integrals, and reviews how to parameterize curves to evaluate line integrals. It also covers Cauchy's theorem, which states that the line integral of an analytic function around a closed curve in its domain is zero. The fundamental theorem of calculus for complex variables and the Cauchy integral formula are also summarized.

1.  ntegration in the Complex Plane
Property of Amit Amola. Should be used
for reference and with consent.
1
Prepared by:
Amit Amola
SBSC(DU)

2. Defining Line Integrals in the Complex Plane
0a z
Nb z
1z
2z
1
3z
2
3
N
1Nz 
nz
n
x
y
#.  𝑛 𝑜𝑛 𝐶 𝑏𝑒𝑡𝑤𝑒𝑒𝑛 𝑧 𝑛−1 𝑎𝑛𝑑 𝑧 𝑛
#. 𝐶𝑜𝑛𝑠𝑖𝑑𝑒𝑟 𝑡ℎ𝑒 𝑠𝑢𝑚𝑠
𝐼 𝑛 = 𝑛=1
𝑁
𝑓( 𝑛)(𝑧 𝑛 − 𝑧 𝑛−1)
#. 𝐿𝑒𝑡 𝑡ℎ𝑒 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑠𝑢𝑏𝑑𝑖𝑣𝑖𝑠𝑖𝑜𝑛𝑠 𝑁 → ∞,
𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡 ∆𝑧 𝑛= 𝑧 𝑛 − 𝑧 𝑛−1 → 0 𝑎𝑛𝑑 𝑑𝑒𝑓𝑖𝑛𝑒
𝐼 =
𝑎
𝑏
𝑓 𝑧 𝑑𝑧 = lim
𝑁→∞
𝐼 𝑁
= lim
𝑁→∞
𝑛=1
𝑁
𝑓( 𝑛)(𝑧 𝑛 − 𝑧 𝑛−1)
(𝑟𝑒𝑠𝑢𝑙𝑡 𝑖𝑠 𝑖𝑛𝑑𝑒𝑝𝑒𝑛𝑑𝑒𝑛𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑑𝑒𝑡𝑎𝑖𝑙𝑠 𝑜𝑓 𝑡ℎ𝑒 𝑝𝑎𝑡ℎ 𝑠𝑢𝑏𝑑𝑖𝑣𝑖𝑠𝑖𝑜𝑛)
C
Property of Amit Amola. Should be used
for reference and with consent.
2

3. Equivalence Between Complex and Real Line Integrals
Note that-
So the complex line integral is equivalent to two real line integrals on C.
Property of Amit Amola. Should be used
for reference and with consent.
3

4. Review of Line Integral Evaluation
t
t
-a a t
-a a
1t
2t 3t
1Nt C
nt
x
y
0t
f Nt t
1t 2t 3t 1Nt nt
… …
0t f Nt t
t
A line integral written as
is really a shorthand for:
where t is some parameterization of C :
or
Example- Parameterization of the circle x2 + y2 = a2
1) x= a cos(t), y= a sin(t), 0 t(=) 2
2) x= t, y= 𝑎2 − 𝑡2, t0 = 𝑎, tf = −a
And x= t, y=− 𝑎2 − 𝑡2, t0 = −𝑎, tf = a
}
(𝒙 𝒕 , 𝒚 𝒕 )
Property of Amit Amola. Should be used
for reference and with consent.
4

5. Review of Line Integral Evaluation, cont’d
1t
2t
3t
1Nt 
C
nt
x
y
0t
f Nt t
While it may be possible to parameterize C(piecewise) using x
and/or y as the independent parameter, it must be remembered
that the other variable is always a function of that parameter i.e.-
(x is the independent parameter)
(y is the independent parameter)
(𝒙 𝒕 , 𝒚 𝒕 )
Property of Amit Amola. Should be used
for reference and with consent.
5

6. Line Integral Example
Consider-
x
y
C

r
z z
It’s a useful result and a
special case of the
“residue theorem”
𝑄. 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒
𝑐
𝑧 𝑛 𝑑𝑧 , 𝑤ℎ𝑒𝑟𝑒
𝐶: 𝑥 = 𝑟𝑐𝑜𝑠𝜃, 𝑦 = 𝑟𝑠𝑖𝑛𝜃, 0 ≤ 𝜃 ≤ 2𝜋
⟹ 𝑧 = 𝑟𝑐𝑜𝑠𝜃 + 𝑖𝑟𝑠𝑖𝑛𝜃 = 𝑟𝑒 𝑖𝜃
,
⟹ 𝑑𝑧 = 𝑟𝑖𝑒 𝑖𝜃
𝑑𝜃
Property of Amit Amola. Should be used
for reference and with consent.
6

7. Cauchy’s Theorem
x
y
C
#. Cauchy′
s Theorem: If 𝑓 z is analytic in R then
𝐶
𝑓 𝑧 𝑑𝑧 = 0
#. First, note that if 𝑓 𝑧 = 𝑤 = 𝑢 + 𝑖𝑣, then
𝐶
𝑓 𝑧 𝑑𝑧 =
𝐶
(𝑢𝑑𝑥 − 𝑣𝑑𝑦) + 𝑖
𝐶
𝑣𝑑𝑥 + 𝑢𝑑𝑦 ;
….. 𝑛𝑜𝑤 𝑤𝑒 𝑤𝑖𝑙𝑙 𝑢𝑠𝑒 𝑎 𝑤𝑒𝑙𝑙 − 𝑘𝑛𝑜𝑤𝑛 𝑣𝑒𝑐𝑡𝑜𝑟 𝑎𝑛𝑎𝑙𝑦𝑠𝑖𝑠 𝑟𝑒𝑠𝑢𝑙𝑡 𝑡𝑜 𝑝𝑟𝑜𝑣𝑒 𝑜𝑢𝑟 𝑡ℎ𝑒𝑜𝑟𝑒𝑚:
R- a simply connected region
Construst vectors 𝐀 = 𝑢 𝒙 − 𝑣 𝒚, … 𝑩 = 𝑣 𝒙 + 𝑢 𝒚 , dr = 𝑑𝑥 𝒙 + 𝑑𝑦 𝒚 ,
in the 𝑥𝑦 plane and write the above equation as:
𝐶
𝑓(𝑧) 𝑑𝑧 =
𝐶
𝑨. 𝑑𝒓 + 𝑖
𝐶
𝑩. 𝑑𝒓 =
𝑖𝑛𝑡𝑒𝑟𝑖𝑜𝑟 𝑜𝑓 𝐶
𝛻 × 𝑨. 𝒛𝑑𝑆 + 𝑖
𝑖𝑛𝑡𝑒𝑟𝑖𝑜𝑟 𝑜𝑓 𝐶
𝛻 × 𝑩. 𝒛𝑑𝑆, 𝑏𝑢𝑡
𝒛. 𝛻 × 𝑨 = 𝒛.
𝒙 𝒚 𝒛
𝜕
𝜕𝑥
𝜕
𝜕𝑦
𝜕
𝜕𝑧
𝑢 −𝑣 0
= −
𝜕𝑣
𝜕𝑥
−
𝜕𝑢
𝜕𝑦
= 0, 𝒛. 𝛻 × 𝑩 = 𝒛.
𝒙 𝒚 𝒛
𝜕
𝜕𝑥
𝜕
𝜕𝑦
𝜕
𝜕𝑧
𝑣 𝑢 0
=
𝜕𝑢
𝜕𝑥
−
𝜕𝑣
𝜕𝑦
= 0
⟹
𝐶
𝑓 𝑧 𝑑𝑧 = 0
Stoke’s
theorem
C.R.
Condition
C.R.
ConditionProperty of Amit Amola. Should be used
for reference and with consent.
7

8. Cauchy’s Theorem(cont’d)
x
y
C
Consider R- a simply connected region
#. Cauchy′s Theorem:
If 𝑓 z is analytic in R then
𝐶
𝑓 𝑧 𝑑𝑧 = 0
#. The proof using Stoke′s theorem requires that u x, y , v x, y have
continuous first derivatives and that C be smooth …
#. But the Goursat proof removes these restrictions; hence the theorem
is often called the Cauchy − Goursat theorem
Property of Amit Amola. Should be used
for reference and with consent.
8

9. Extension of Cauchy’s Theorem to Multiply-Connected
Regions
x
y
1C2C
1c
2c
x
y
1C2C
R- a multiply connected region
R’- a simply connected region
#. If 𝑓 𝑧 is analytic in R then:
𝐶1,2
𝑓 𝑧 𝑑𝑧 =?
#. Introduce an infinitesimal- width “bridge” to make R into a simply
connected region R’
𝐶1−𝐶2−𝑐1+𝑐2
𝑓 𝑧 𝑑𝑧 =
𝐶1
𝑓 𝑧 𝑑𝑧 −
𝐶2
𝑓 𝑧 𝑑𝑧 = 0
#. It shows that integrals are independent of path.
(since integrals along 𝑐1 and 𝑐2 are in opposite
directions and thus cancel each other)
Property of Amit Amola. Should be used
for reference and with consent.
9

10. Fundamental Theorem of the Calculus of Complex Variables
az
bz
1z
2z 3z
1Nz C
nz
x
y
1z
2z
3z
Nz
𝑧 𝑎
𝑧 𝑏
𝑓 𝑧 𝑑𝑧 is a path independent in a simply connected region R
𝑧 𝑎
𝑧 𝑏
𝑓 𝑧 𝑑𝑧 = lim
𝑁→∞
𝑛=1
𝑁
𝑓  𝑛 ∆𝑧 𝑛 , ∆𝑧 𝑛 = 𝑧 𝑛 − 𝑧 𝑛−1,
 𝑛 on C between zn−1 and zn
Suppose we can find 𝐹 z such that 𝐹′ z
=
𝑑𝐹
𝑑𝑧
= 𝑓 𝑧 ; hence 𝑓  𝑛 ≈
Δ𝐹𝑛
Δ𝑧 𝑛
=
𝐹 𝑧 𝑛 − 𝐹(𝑧 𝑛−1)
∆𝑧 𝑛
= 𝐹 𝑧 𝑏 − 𝐹 𝑧 𝑎 (path independent if 𝑓 𝑧 is analytic on the paths from 𝑧 𝑎 𝑡𝑜 𝑧 𝑏)
⇒
Property of Amit Amola. Should be used
for reference and with consent.
10

11. Fundamental Theorem of the Calculus of Complex Variables
(cont’d)
#. Fundamental Theorem of Calculus:
Suppose we can find 𝐹 𝑧 such that 𝐹′
𝑧 =
𝑑𝐹
𝑑𝑧
= 𝑓 𝑧 :
⟹
𝑧 𝑎
𝑧 𝑏
𝑓 𝑧 𝑑𝑧 =
𝑧 𝑎
𝑧 𝑏
𝑑𝐹
𝑑𝑧
𝑑𝑧 = 𝐹 𝑧 𝑏 − 𝐹 𝑧 𝑎
#. This permits us to define indefinite integrals:
𝑧 𝑛
𝑑𝑧 =
𝑧 𝑛+1
𝑛 + 1
, sin 𝑧 𝑑𝑧 = − cos 𝑧, 𝑒 𝑎𝑧
𝑑𝑧 =
𝑒 𝑎𝑧
𝑎
, 𝑒𝑡𝑐
#. In general
F(z)=
𝑧0
𝑧
𝑓  𝑑 for arbitrary 𝑧0
#. All the indefinite integrals differ by only a constant.
Property of Amit Amola. Should be used
for reference and with consent.
11

12. Cauchy Integral Formula
x
y
C
R
0z
0C
1c2c
x
y
C
R- a simply connected region
#. 𝑓 𝑧 is assumed analytic in R but we multiply by a factor
1
𝑧 − 𝑧0
that is analytic
except at 𝑧0 and consider the integral around 𝐶
𝐶
𝑓(𝑧)
(𝑧 − 𝑧0)
𝑑𝑧
#. To evaluate, consider the path 𝐶 + 𝑐1 + 𝑐2 + 𝐶0 shown that encloses a simply −
connected region for which the integrand is analytic on and inside the path:
𝐶+𝑐1+𝑐2+𝐶0
𝑓(𝑧)
(𝑧 − 𝑧0)
𝑑𝑧 = 0 ⟹
𝐶
𝑓(𝑧)
(𝑧 − 𝑧0)
𝑑𝑧 = −
𝐶0
𝑓(𝑧)
(𝑧 − 𝑧0)
𝑑𝑧
Property of Amit Amola. Should be used
for reference and with consent.
12

13. Cauchy Integral Formula, cont’d
   
0
0 0C C
f z f z
dz dz
z z z z
 
  
0z
0C
C
Evaluate the 𝐶0 integral on a circular path,
for r ⟶ 0
⇒ ⇒
Cauchy Integral
Formula
The value of 𝑓 𝑧 at 𝑧0 is completely determined by its values on 𝐶!
Property of Amit Amola. Should be used
for reference and with consent.
13

14. Cauchy Integral Formula, cont’d
0z
0C
C
0z
C
Note that if 𝑧0 is outside C, the integrand is analytic inside C, hence by the
Cauchy Integral Theorem,
1
2𝜋𝑖
𝐶
𝑓(𝑧)
𝑧 − 𝑧0
𝑑𝑧 = 0
In summary,
𝐶
𝑓(𝑧)
𝑧 − 𝑧0
𝑑𝑧 =
2𝜋𝑖 𝑓 𝑧0 , 𝑧0 inside 𝐶
0, 𝑧0 outside 𝐶
Property of Amit Amola. Should be used
for reference and with consent.
14

15. Derivative Formula
0z
C
Since 𝑓(𝑧) is analytic in C , its derivative exists;
let’s express it in terms of the Cauchy Formula:
𝑓 𝑧0 =
1
2𝜋𝑖
𝐶
𝑓(𝑧)
𝑧 − 𝑧0
𝑑𝑧
.So
⇒
⇒
⇒ We’ve also just proved we can differentiate
w.r.t. 𝑧0 under the integral sign!Property of Amit Amola. Should be used
for reference and with consent.
15

16. Derivative Formulas, cont’d
0z
C
If 𝑓(𝑧) is analytic in C, then its derivatives of all orders exist,
and hence they are analytic as well.
In general,
Similarly
or
⇒Property of Amit Amola. Should be used
for reference and with consent.
16