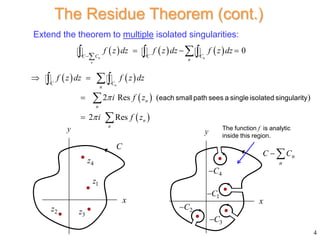
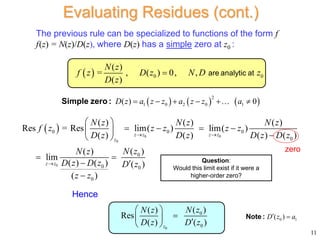
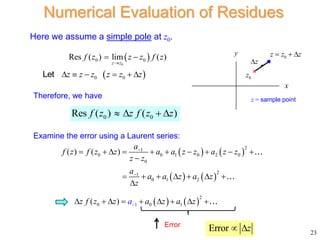
The residue theorem states that for a function f(z) that is analytic within and on a closed contour C except for isolated singularities, the integral of f(z) around C is equal to 2πi times the sum of the residues of f(z) at the singularities enclosed by C. The residue of a simple pole is the coefficient of the (z-z0)-1 term in the Laurent series expansion of f(z) about z0. For a function that is a ratio of two functions, where the denominator has a simple zero, the residue can be calculated as the limit of the numerator over the derivative of the denominator as z approaches the zero.

1. The Residue Theorem
and Residue Evaluation
ECE 6382
Notes are from D. R. Wilton, Dept. of ECE
1
David R. Jackson
Fall 2023
Notes 10

2. The Residue Theorem
Consider a line integral
about a path enclosing an
isolated singular point:
 
C
I f z dz
 
Expand f (z) in a Laurent series,
deform the contour C to a circle of
(arbitrary) radius r centered at z0
that stays inside C, and evaluate
the integral:
 
2
1 ( 1)
0
0, 1
0
1
1
2
2
n i n
n
C
n
n
f z dz i a r e d
i a r
i a






 

 






 
2
The path C stays in a region
where f is analytic (except at z0).
   
0
n
n
n
f z a z z


 

0 , ,
i i
z z re dz rie d
 

  
Let
Note:
For a Laurent series we can integrate term-by-term
(switch the order of integration and summation) in the
region of convergence, due to uniform convergence.
x
y C
r
0
z

3. The value a-1 corresponding to an isolated singular point z0
is called the residue of f(z) at z0.
   
0
2 Res
C
I f z dz i f z

 

Note:
The path orientation is
assumed counterclockwise.
3
The Residue Theorem (cont.)
 
   
     
2 3
3 2
0 1 0 2 0 3 0
3 2
0
0 0
1
a a
f z a a z z a z z a z z
z z
z z
a
z z
 

           

 
Residue
Laurent series expansion:

4. Extend the theorem to multiple isolated singularities:
      0
n n
n
C C C C
n
f z dz f z dz f z dz

  
 
  
4
The Residue Theorem (cont.)
   
 
 
2 Res ( )
2 Res
n
C C
n
n
n
n
n
f z dz f z dz
i f z
i f z


 



 


each small path sees a single isolated singularity
The function f is analytic
inside this region.
n
n
C C
 
1
C

2
C

3
C

4
C

x
y
x
y
C
1
z
2
z
3
z
4
z

5. Alternatively, shrink the path, leaving only the singularities encircled:
Isolated singularities at zn
   
 
 
2 Res ( )
2 Res
n
C C
n
n
n
n
n
f z dz f z dz
i f z
i f z






 


each small path sees a single isolated singularity
5
The Residue Theorem (cont.)
x
y
C
4
C
1
C
2
C
3
C

6. Summary of Residue Theorem
Isolated singularities at zn
   
2 Res n
C
n
f z dz i f z

 

6
The Residue Theorem (cont.)
x
y
z1
C
z4
z3
z2
Note: The integral is taken counterclockwise.
The integral is equal to 2 i times the sum of the residues at the singularities.
A function f is an analytic within C except at isolated singularities.

7. Note that the residue theorem subsumes several of our
earlier results and theorems:
   
0
C
f z dz f z C

 if analytic (noisolatedsingularities) in
 
 
0
0
0
.
2 ( )
C
C
z
f z
dz i f z f z C
z z




(Hence is the only isolated singularity in )
if analytic in
7
The Residue Theorem (cont.)
Cauchy Integral Formula:
Cauchy’s Theorem:
   
 
 
 
 
1
0 0 0 0
0 0
0 0
n n
n n
n n
f z f z
f z b z z b z z b f z
z z z z
 

 
 
       
 
 
 
  Residue
Note:

8. Evaluating Residues
 Construct Laurent series about each singularity zn, and
then identify the coefficient a-1,n= Res f(zn).
   
0 0
1
0 0 0 1 0
0
1
lim ( ) lim ( )
z z z z
a
z z f z z z a a z z
z z
a

 

 
      
 

 

 
0
0 0
Res ( ) lim ( )
z z
f z z z f z

 
8
 For a simple pole at z = z0 we have a simple formula:
 Sometimes this can be a tedious approach.
Question:
Would this limit exist if it were a
higher-order pole?

9.  
2
2
2
( ) 2, ,
( 2)( 1)
Res ( 2) lim 2
z
z
f z z i i
z z
f z

    
 
  
has poles at
simple
2
( 2)
z
z 
 
2
4
5
( 1)
Res ( ) lim
z i
z
f i z i

 

 
 
2
( 2)( )
z
z z i z i
  
2i

( 2) 2
i i

 
2
5
Res ( ) lim
z i
i
f i z i



  
 
2
( 2)( )
z
z z i z i
  
( 2 )
i


( 2) ( 2 )
i i
  
2
5
i


Example:
9
Evaluating Residues (cont.)

10. Example:
 
1
( ) , 0, 1, 2,
sin
1 1
Res ( ) lim( ) lim 1
sin cos
1 1
Res ( ) lim( ) lim ( )
sin sin( )
1
lim ( )
sin(
n
z n z n
z n z n
z n
f z z n n
z
f n z n
z z
f n z n z n
z z n n
z n
z n
 
 


 
  
 


 
 

    
     
   
 
 

has simple poles at
Alternatively,
L'Hospital's
rule
  0
)cos cos( )sin
( )
lim 1 lim 1
sin( )cos sin
n
z n w
n z n n
z n w
z n n w

  

 
 
 

   

since we already know
10
Evaluating Residues (cont.)
 
Res ( ) 1
n
f n  

11. The previous rule can be specialized to functions of the form f
f(z) = N(z)/D(z), where D(z) has a simple zero at z0 :
 
0 0
0
0
0 0 0
0
0
0 0
0
( ) ( ) ( )
Res = Res lim( ) lim( )
( ) ( ) ( ) ( )
( )
( )
lim
( ) ( ) ( )
( )
z z z z
z
z z
N z N z N z
f z z z z z
D z D z D z D z
N z
N z
D z D z D z
z z
 

 
   
 

 
 
 

0
0
0
( )
( )
Res
( ) ( )
z
N z
N z
D z D z
 

  
 
11
Evaluating Residues (cont.)
zero
Hence
  0 0
( )
= , ( ) 0, ,
( )
N z
f z D z N D z
D z
 are analytic at
Question:
Would this limit exist if it were a
higher-order zero?
     
2
1 0 2 0 1
( ) 0
D z a z z a z z a
     
Simple zero :
0 1
( )
D z a
 
Note :

12. Example:
 
 
 
2 1
2
2 1
sin
tan ,
cos 2
0, 1, 2,
sin
Res tan
n
n
z
z z
z
n
z




 
  
 
has simple poles at
for
 
2 1
2
sin
n 


1
 
12
Evaluating Residues (cont.)
  tan
f z z

 
 
2 1
Res tan 1, , 0, 1, 2,
2
n
z z n


     

13. Including a Multiplying Function
13
Evaluating Residues (cont.)
     
f z A z F z

 
 
0
0
A z z
F z z


analytic function at
function with simple pole at
         
 
 
0 0 0
0
1
0 0 0 0 0 1 0
0
1 0 0
0 1
Res ( ) lim ( ) lim ( ) lim ( )
lim ( )
( )
z z z z z z
z z
b
f z z z f z z z A z F z z z A z b b z z
z z
A z b b z z
A z b

  



 
         
 

 
   

 
0 0 0
Res ( ) ( )Res
f z A z F z

Hence, we have:
 
F z

14. 2
1
0 1 0 2 0
1
0 0 0
0 1
1
0 0
1
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( ) ( )
m m
m m
m
m m
a a
f z a a z
a
z a z z
z z z z z z
z z f z a a
a
z z z z

 
  

 
         
  
      
At the pole, the Laurent series is
Hence the following series is a Taylor series about the pole:
 
1
0 0
1
0
1
0
1 1
0
( )
( )
1
( ) ( )
1 !
m m
m
m
m
m
a z z
z z
d
z z f z
m dz z z
a




  

 
 
 
 
A formula for the coefficent of is
For a non-simple pole of finite order m at z = z0:
 
1
0 0
1
0
1
Res ( ) ( ) ( ) (
1 !
m
m
m
d
f z z z f z m
m dz z z


 
 
 
 
finite)
14
Evaluating Residues (cont.)
     
   
3
0 3 2 0
2 3
0 0 0
1
z z f z a a z z
z z a z z
a
 
   
    
Example (m = 3):

15. For a non-simple pole of finite order m at z = z0:
15
Evaluating Residues (cont.)
 
0
,
0
lim ( ) 0,
,
m
p
z z
a p m
L z z f z p m
p m





   

 

1 1
0 0 1 0 1 0 0 0
( ) ( ) ( ) ( ) ( ) ( )
p p m p m p p
m m
z z f z a z z a z z a z z a z z
   
   
          
Proof:
2
1 1
0 1 0 2 0
1
0 0 0
( ) ( ) ( )
( ) ( ) ( )
m m
m m
a a a
f z a a z z a z z
z z z z z z
   

         
  
A test to find the order m of a pole:
0
m
a 
where

16.  
1
0 0
1
0
1
Res ( ) ( ) ( ) (
1 !
m
m
m
d
f z z z f z m
m dz z z


 
 
 
 
finite)
Example:
2
3
2
3
2
2
( ) 3 2
( 2)
1
Res ( 2) ( 2)
2!
z z
f z z
z
d
f z
dz

  

   
has a pole of order at
2
3
2
( 2)
z z
z


2
2
2
2
1 4
2 2
2! 2!
2
z
d
z z
dz z
 
 
 
   
 
   
 

16
Evaluating Residues (cont.)
Res ( 2) 2
f  

17. Example:
2
2 2 2
2 4
2
3
1
( ) 2 , 0, 1, 2,
sin
1 ( ) 2( )sin 2( ) sin cos
Res ( )
1! sin sin
2( )sin 2( ) cos
sin
f z z n n
z
d z n z n z z n z z
f n
dz z z
z n z n
z n z z n z
z z n

  

 
 

    
   
   
  
   
   
 
 
  
  
  
has poles of o de
r at
r
17
Evaluating Residues (cont.)
After three applications of L’Hospital’s rule:
Res ( ) 0
f n 

18.  
 
2 2 2 2
3 5 2 4
2
2 4 6 2 4 6
2
2
2
2
2
2 2
2
1 1 1 1
( )
sin sin ( ) sin ( ) sin
1 1
1
3! 5! 3! 5!
1
1
3! 5! 7! 3! 5! 7!
1 1 1
1
3! 5! 3!
f z u z n
z z n n z n u
u u u u
u u
u u u u u u
u
u
u

  
     
  
 
   
     
   
   
 
   
 
       
   
 
   
 

    



Geometric
Series
1
4
2
2
Residue=0
!
1 2
3
u
a
u
u

 


   
 


 

 
missing term
18
Evaluating Residues (cont.)
Alternative calculation:
Res ( ) 0
f n 
Note:
A simple shift
does not affect the
residue (we have
the same
coefficients in the
Laurent series)

19. Example:
1/
( ) z
f z e
 (essential singularity at z = 0)
2 3
1/ 1 1 1 1 1
1
2! 3!
z
e
z z z
   
    
   
   
1 1
a 
Residue:
19
Evaluating Residues (cont.)
Res (0) 1
f 

20. Summary of Residue Formulas
20
Evaluating Residues (cont.)
 
0
1
0 0
1
1
Res ( ) lim ( ) ( )
1 !
m
m
m
z z
d
f z z z f z
m dz



 
 
 

 
0
0
0
( )
( )
Res ( ) 0
( ) ( )
N z
N z
D z
D z D z
 
 
  
 
simple zero
if
 
0
0 0
Res ( ) lim ( )
z z
f z z z f z

  Simple pole
Simple pole
Pole of order m

21. Extension for simple poles (going halfway around)
As   0:
 
0 0
1
1 1 1 1
0 0
i
i
C C
a dz i e
dz a a d a id a i
z z z z e
 


 

  


   
 
   
 
   
Residue term:
Proof:
21
Evaluating Residues (cont.)
   
0
0
Res
C
f z dz i f z






Note:
If it is not a simple pole, the
integral around the small
semicircle may tend to infinity.
0
i
z z e

 
0
z
C

x
y We go halfway around on an
infinitesimal semicircle.

   
0
1
1
0
1: 0
n i n
n
n n
C
n a z z dz ia e d



 



    
 
For Note: For n < -1 the integral
does not converge!

22. Similarly, if we go in the opposite direction:
22
Evaluating Residues (cont.)
As   0:
0
z
C

x
y
Clockwise

   
0
0
Res
C
f z dz i f z






Extension for simple poles (going halfway around)

23. 23
Numerical Evaluation of Residues
Here we assume a simple pole at z0.
 
0
0 0
Res ( ) lim ( )
z z
f z z z f z

 
0 0
Res ( ) ( )
f z z f z z
   
 
0 0
z z z z z z
     
Let
   
   
2
1
0 0 1 0 2 0
0
2
1
0 1 2
( ) ( )
a
f z f z z a a z z a z z
z z
a
a a z a z
z


         

      

Therefore, we have
Examine the error using a Laurent series:
   
1
2
0 0 1
( ) a
z f z z a z a z

        
Error
Error z
 
x
y
0
z
0
z z z
  
z


z = sample point

24. 24
Numerical Evaluation of Residues (cont.)
We can improve this by using two sample points and averaging:
1 0 1 2 0 2
0
( ) ( )
Res ( )
2
z f z z z f z z
f z
      
 
  
 
x
y
0
z
0
z z
 
z


0
z z
 
1 2
,
z z z z
     
0 0
0
( ) ( )
Res ( )
2
f z z f z z
f z z
    
 
   
 
Choose
This is a “central-difference” formula.

25. 25
Numerical Evaluation of Residues (cont.)
Examine the error using a Laurent series:
Error
2
Error z
 
x
y
0
z
0
z z
 
z


0
z z

 
   
2
1
0 0 1 2
2
1
0 0 1 2
( )
( )
a
f z z a a z a z
z
a
f z z a a z a z
z


        

        

 
2
0 0
1 1
( ) ( )
2
f z z f z z
z a a z

    
 
    
 
 
0 0
0
( ) ( )
Res ( )
2
f z z f z z
f z z
    
 
   
 

26. 26
Numerical Evaluation of Residues (cont.)
We can improve this even more by using four sample points:
/2 /2 2 /2 2 /2 3 /2 3 /2
0 0 0 0
0
( ) ( ) ( ) ( )
Res ( )
4
i i i i i i
z f z z ze f z e z ze f z e z ze f z e z
f z
     
              

Examine the error using a Laurent series:
     
     
     
2 3
1
0 0 1 2 3
2 3
/2 /2 /2 /2
1
0 0 1 2 3
/2
2 3
2 /2 2 /2 2 /2 2 /2
1
0 0 1 2 3
2 /2
3 /2 3
1
0 0 1
3 /2
( )
( )
( )
( )
i i i i
i
i i i i
i
i i
i
a
f z z a a z a z a z
z
a
f z ze a a ze a ze a ze
ze
a
f z ze a a ze a ze a ze
ze
a
f z ze a a ze
ze
   

   







          

          

          

     

     
2 3
/2 3 /2 3 /2
2 3
i i
a ze a ze
  
    
 
/2 /2 2 /2 2 /2 3 /2 3 /2
4
0 0 0 0
1 3
( ) ( ) ( ) ( )
4
i i i i i i
f z z e f z e z e f z e z e f z e z
z a a z
     

 
          
    
 
 
4
Error z
 
x
y
0
z
0
z z
 
z


/2
0
i
z e z

 
2 /2
0
i
z e z

 
3 /2
0
i
z e z

 
/2 2 /2 3 /2
1 2 3 4
, , ,
i i i
z z z z e z z e z z e
  
           
We see that

27. 27
Numerical Evaluation of Residues (cont.)
A little more detail:
   
         
         
2 3
1
0 0 1 2 3
2 3 4
2 3
/2 /2 /2 /2 /2 /2
1
0 0 1 2 3
2 3 4
2 3
2 /2 2 /2 2 /2 2 /2 2 /2 2 /2
1
0 0 1 2 3
3 /2 3 /2
0
( )
( )
( )
( )
i i i i i i
i i i i i i
i i
a
f z z a a z a z a z
z
a
e f z ze a e a z e a z e a z e
z
a
e f z ze a e a z e a z e a z e
z
e f z ze
     
     
 



          

          

          

           
2 3 4
2 3
3 /2 3 /2 3 /2 3 /2
1
0 1 2 3
i i i i
a
a e a z e a z e a z e
z
   

        

            
            
            
            
2 3
1
0 0 1 2 3
2 3
/2 /2 1
0 0 1 2 3
2 3
2 /2 2 /2 1
0 0 1 2 3
2 3
3 /2 3 /2 1
0 0 1 2 3
( ) 1 1 1 1
( ) 1 1
( ) 1 1 1 1
( ) 1 1
i i
i i
i i
a
f z z a a z a z a z
z
a
e f z ze a i a z a z i a z
z
a
e f z ze a a z a z a z
z
a
e f z ze a i a z a z i a z
z
 
 
 




          

            

            

            

Simplifying:

28. 28
Numerical Evaluation of Residues (cont.)
In general, we can use N sample points
 
   
 
2 1 / 2 1 /
0 0
1
1
Res ( )
N
i n N i n N
n
f z z e f z e z
N
 
 

   

Error
N
z
 
x
y
0
z
0
z z
 
z


2 /
0
i N
z e z

 
8
N 
 
2 1 /
, 1,2
i n N
n
z ze n N
 
   

29. 29
Numerical Evaluation of Residues (cont.)
We can also numerically integrate around a simple pole:
 
0
1
Res ( )
2 C
f z f z dz
i

 
 
2
0 0
0
Res ( )
2
i i
r
f z f z re e d

 


 

Use the midpoint rule of integration:
Choose a small circle of radius r:
0
i
i
z z re
dz ire d



 

2 1
, 1,2
2
n n n N
N


 
  
 
 
Sample points:
x
y
0
z

C
r
0 2
1
 N

2
N


 
N intervals

30. 30
Numerical Evaluation of Residues (cont.)
We then have
 
2
0 0
0
Res ( )
2
i i
r
f z f z re e d

 


 

 
   
2 1/2 / 2 1/2 /
0 0
1
2
Res ( )
2
N
i n N i n N
n
r
f z f z re e
N
  

 

 
   
 

 
 
/
2 / / 2 /
0 0
1
Res ( )
i N N
i n N i N i n N
n
re
f z f z r e e e
N

  



 

 
2 / 2 /
0
0 0 0
1
Res ( )
N
i n N i n N
n
z
f z f z z e e
N
 


  
 /
0
i N
z re 

 
where
or
or
Sample
0 2
0
 1
N
 
2
N


 
2 1
, 1,2
2
n n n N
N


 
  
 
 

31. 31
Numerical Evaluation of Residues (cont.)
We then have
   
2 / 2 /
0 0 0 0
1
1
Res ( )
N
i n N i n N
n
f z z e f z z e
N
 

   

This is the same result that we obtained from the sampling method!
Note:
The midpoint rule is exceptionally accurate when applied to a smooth
periodic function, integrating over a period*.
*J. A. C. Wiedeman, “Numerical Integration of Periodic Functions: A Few Examples,” The
Mathematical Association of America, vol. 109, Jan. 2002, pp. 21-36.
 
   
 
2 1 / 2 1 /
0 0
1
1
Res ( )
N
i n N i n N
n
f z z e f z z e
N
 
 

   

or
(We have the same
set of sample points if
n is replaced by n-1.)