Engg. mathematics iii

Functions of a Complex Variable
Dr. M K Singh
Associate Professor
Jahangirabad Institute of Technology,
Barabanki

Functions of A Complex Variables I
Functions of a complex variable provide us some powerful and
widely useful tools in theoretical physics.
• Some important physical quantities are complex variables (the
wave-function )
• Evaluating definite integrals.
• Obtaining asymptotic solutions of differentials
equations.
• Integral transforms
• Many Physical quantities that were originally real become complex
as simple theory is made more general. The energy
(  the finite life time).
 iEE nn
0
/1

We here go through the complex algebra briefly.
A complex number z = (x,y) = x + iy, Where.
We will see that the ordering of two real numbers (x,y) is significant,
i.e. in general x + iy  y + ix
X: the real part, labeled by Re(z); y: the imaginary part, labeled by Im(z)
Three frequently used representations:
(1) Cartesian representation: x+iy
(2) polar representation, we may write
z=r(cos  + i sin) or
r – the modulus or magnitude of z
 - the argument or phase of z
1i
i
erz 

r – the modulus or magnitude of z
 - the argument or phase of z
The relation between Cartesian
and polar representation:
The choice of polar representation or Cartesian representation is a
matter of convenience. Addition and subtraction of complex variables
are easier in the Cartesian representation. Multiplication, division,
powers, roots are easier to handle in polar form,
 
 
1/ 22 2
1
tan /
r z x y
y x 
  

 21
2121
 
 i
errzz
   21
2121 //  
 i
errzz
innn
erz 
z1 ± z2 = (x1 ± x2 )+i(y1 ± y2 )
z1z2 = (x1x2 - y1y2 )+i(x1y2 + x2y1)

From z, complex functions f(z) may be constructed. They can be
written
f(z) = u(x,y) + iv(x,y)
in which v and u are real functions.
For example if , we have
The relationship between z and f(z) is best pictured as a
mapping operation, we address it in detail later.
)arg()arg()arg( 2121 zzzz 
2121 zzzz 
    xyiyxzf 222

Using the polar form,
2
)( zzf 

Function: Mapping operation
x
y Z-plane
u
v
The function w(x,y)=u(x,y)+iv(x,y) maps points in the xy plane into points
in the uv plane.
nin
i
ie
ie
)sin(cos
sincos






We get a not so obvious formula
Since
n
inin )sin(cossincos  

Complex Conjugation: replacing i by –i, which is denoted by (*),
We then have
Hence
Note:
ln z is a multi-valued function. To avoid ambiguity, we usually set n=0
and limit the phase to an interval of length of 2. The value of lnz with
n=0 is called the principal value of lnz.
iyxz *
222*
ryxzz 
  21*
zzz  Special features: single-valued function of a
real variable ---- multi-valued function
i
rez    ni
re 2
 irlnzln   nirz 2lnln 

Another possibility


evenand1|cos||,sin|possiblyhowever,
x;realafor1|cos||,sin|
zz
xx
Question:
yx
yx
yxiyxiyx
yxiyxiyx
i
ee iziz
222
222
iziz
sinhcos|cosz|
sinhsin|sinz|(b)
sinhsincoshcos)cos(
sinhcoscoshsin)sin((a)showto
2
e
sinz;
2
e
cosz
:identitiestheUsing










Analytic functions
If f(z) is differentiable at and in some small region around ,
we say that f(z) is analytic at
Differentiable: Cauthy-Riemann conditions are satisfied
the partial derivatives of u and v are continuous
Analytic function:
Property 1:
Property 2: established a relation between u and v
022
 vu
Example:
Find the analytic functions w(z) = u(x, y)+iv(x, y)
if (a) u(x, y) = x3
-3xy2
;(v = 3x3
y- y3
+c)
(b) v(x, y) = e-y
sin x;(v = ?)
0zz 
0zz 
0z

Cauchy-Riemann Equations
     
 
   
 
0 0 0
0 0
0
0
0
1 0 0
2 0 0
Let , , be diff. at
then lim exists
with
In particular, can be computed along
: , i.e.
: , i.e.
z
f z u x y iv x y z x iy
f z z f z
f z
z
z x i y
f z
C y y x x z x
C x x y y
 
   
  
 

    

    
  z i y


 

 
0 0 0 0
0
0 0 0 0
( , ) ( , )
( , ) ( , )
u v
x y i x y
x x
f z
u v
i x y x y
y y
 
 
     
 

• We have proved the following theorem.
u v
x y
u v
y x
 
 

   
 

Theorem
A necessary condition for a fun.
f(z)=u(x,y)+iv(x,y)
to be diff. at a point z0 is that the C-R eq. hold at
z0.
Consequently, if f is analytic in an open set G,
then the C-R eq. must hold at every point of G.

Application of Theorem
To show that a function is NOT analytic, it
suffices to show that the C-R eq. are not
satisfied

Cauchy – Riemann conditions
Having established complex functions, we now proceed to
differentiate them. The derivative of f(z), like that of a real function, is
defined by
provided that the limit is independent of the particular approach to the
point z. For real variable, we require that
Now, with z (or zo) some point in a plane, our requirement that the
limit be independent of the direction of approach is very restrictive.
Consider
       zf
dz
df
z
zf
z
zfzzf
zz


 



 00
limlim
     o
xxxx
xfxfxf
oo



limlim
yixz  
viuf  
,
yix
viu
z
f








Let us take limit by the two different approaches as in the figure. First,
with y = 0, we let x0,
Assuming the partial derivatives exist. For a second approach, we set
x = 0 and then let y 0. This leads to
If we have a derivative, the above two results must be identical. So,







 x
v
i
x
u
z
f
xz 





 00
limlim
x
v
i
x
u






y
v
y
u
i
z
f
z 





 

 0
lim
y
v
x
u





,
x
v
y
u






These are the famous Cauchy-Riemann conditions. These Cauchy-
Riemann conditions are necessary for the existence of a derivative, that
is, if exists, the C-R conditions must hold.
Conversely, if the C-R conditions are satisfied and the partial
derivatives of u(x,y) and v(x,y) are continuous, exists.
 xf
 zf

Cauchy’s integral Theorem
We now turn to integration.
in close analogy to the integral of a real function
The contour is divided into n intervals .Let
with for j. Then
'
00 zz 
01  jjj zzz
   




0
0
1
lim
z
z
n
j
jj
n
dzzfzf 
n
The right-hand side of the above equation is called the contour (path) integral
of f(z)
.and
bewteencurveon thepointaiswhere
,andpointsthechoosing
ofdetailstheoftindependen
isandexistslimitthat theprovided
1
j
j
jj
j
zz
z



As an alternative, the contour may be defined by
with the path C specified. This reduces the complex integral to the
complex sum of real integrals. It’s somewhat analogous to the case of
the vector integral.
An important example
        
22
11
2
1
,,
yx
yxc
z
zc
idydxyxivyxudzzf
     
22
11
22
11
yx
yx
yx
yxcc
udyvdxivdyudx

c
n
dzz
where C is a circle of radius r>0 around the origin z=0 in the
direction of counterclockwise.

In polar coordinates, we parameterize
and , and have
which is independent of r.
Cauchy’s integral theorem
– If a function f(z) is analytical (therefore single-valued) [and its partial
derivatives are continuous] through some simply connected region R, for
every closed path C in R,

 i
rez
 
diredz i
   
 


2
0
1
1exp
22
1
dni
r
dzz
i
n
c
n
1-nfor1
-1nfor0
{



  0 dzzf
c

•Multiply connected regions
The original statement of our theorem demanded a simply connected
region. This restriction may easily be relaxed by the creation of a
barrier, a contour line. Consider the multiply connected region of
Fig.1.6 In which f(z) is not defined for the interior R
Cauchy’s integral theorem is not valid for the contour C, but we can
construct a C for which the theorem holds. If line segments DE and
GA arbitrarily close together, then
    
E
D
A
G
dzzfdzzf

'
2
'
1 CEFGCABD 
 
 
 dzzfdzzf
EFGGADEABD
ABDEFGA
C








 
  0dzzf
EFGABD






 
    

21 CC
dzzfdzzf

Cauchy’s Integral Formula
Cauchy’s integral formula: If f(z) is analytic on and within a closed contour C
then
in which z0 is some point in the interior region bounded by C. Note that
here z-z0 0 and the integral is well defined.
Although f(z) is assumed analytic, the integrand (f(z)/z-z0) is not
analytic at z=z0 unless f(z0)=0. If the contour is deformed as in Fig.1.8
Cauchy’s integral theorem applies.
So we have
   0
0
2 zif
zz
dzzf
C


   
  



C C
dz
zz
zf
zz
dzzf
2
0
00

Let , here r is small and will eventually be made to
approach zero
(r0)
Here is a remarkable result. The value of an analytic function is given at
an interior point at z=z0 once the values on the boundary C are
specified.
What happens if z0 is exterior to C?
In this case the entire integral is analytic on and within C, so the
integral vanishes.

 i
0 rezz
    


drie
re
rezf
dz
zz
dzzf i
C C
i
i
 



2 2
0
0
   00 2
2
zifdzif
C
  

Derivatives
Cauchy’s integral formula may be used to obtain an expression for
the derivation of f(z)
Moreover, for the n-th order of derivative
 
 
0
0 0
1
2
f z dzd
f z
dz i z z
 
   
 
Ñ
   
 




C
zf
zz
dzzf
i exteriorz,0
interiorz,
2
1
0
00
0
   
  







 2
000 2
11
2
1
zz
dzzf
izzdz
d
dzzf
i 
    
  

 1
0
0
2
!
n
n
zz
dzzf
i
n
zf


.findorigin,about thecirclea
withinandonanalyticisa)(If1.
Examples
0
n
n
n
n
a
zzf 

     jn
jn
nj
j
zaajzf 


1
!
   j
j
ajf !0 
    
 
 12
1
!
0
n
n
n
z
dzzf
in
f
a


In the above case, on a circle of radius r about the origin,
then (Cauchy’s inequality)
Proof:
where
Lowville's theorem: If f(z) is analytic and bounded in the complex
plane, it is a constant.
Proof: For any z0, construct a circle of radius R around z0,
  Mzf 
Mra n
n 
    nn
rz
nn
r
M
r
r
rM
z
dzzf
a  

 11
2
2
2
1



   rfMaxrM rz 
   
  22
0
0
2
22
1
R
RM
zz
dzzf
i
zf
R






R
M


Since R is arbitrary, let , we have
Conversely, the slightest deviation of an analytic function from a
constant value implies that there must be at least one singularity
somewhere in the infinite complex plane. Apart from the trivial constant
functions, then, singularities are a fact of life, and we must learn to live
with them, and to use them further.
R
  .const)z(f,e.i,0zf 

Laurent Expansion
Taylor Expansion
Suppose we are trying to expand f(z) about z=z0, i.e.,
and we have z=z1 as the nearest point for which f(z) is not analytic. We
construct a circle C centered at z=z0 with radius
From the Cauchy integral formula,
   



0n
n
0n zzazf
010 zzzz 
     
    







C 00C
zzzz
zdzf
i2
1
zz
zdzf
i2
1
zf
 
       



C 000 zzzz1zz
zdzf
i2
1

Here z is a point on C and z is any point interior to C. For |t| <1, we
note the identity
So we may write
which is our desired Taylor expansion, just as for real variable power
series, this expansion is unique for a given z0.




 0
2
1
1
1
n
n
ttt
t

 
   
 






C n
n
n
zz
zdzfzz
i
zf
0
1
0
0
2
1

   
  






0
1
0
0
2
1
n C
n
n
zz
zdzf
zz
i
 
  




0
0
0
!n
n
n
n
zf
zz

Schwarz reflection principle
From the binomial expansion of for integer n (as an
assignment), it is easy to see, for real x0
Schwarz reflection principle:
If a function f(z) is (1) analytic over some region including the real axis
and (2) real when z is real, then
We expand f(z) about some point (nonsingular) point x0 on the real axis
because f(z) is analytic at z=x0.
Since f(z) is real when z is real, the n-th derivate must be real.
   n
0xzzg 
        *n
0
**n
0
*
zgxzxzzg 
   **
zfzf 
   
  




0
0
0
!n
n
n
n
xf
xzzf
   
  
 *
0
0
0
**
!
zf
n
xf
xzzf
n
n
n
 



Laurent Series
We frequently encounter functions that are analytic in annular
region

Drawing an imaginary contour line to convert our region into a simply
connected region, we apply Cauchy’s integral formula for C2 and C1,
with radii r2 and r1, and obtain
We let r2 r and r1 R, so for C1, while for C2, .
We expand two denominators as we did before
(Laurent Series)
   
zz
zdzf
i
zf
CC












 
21
2
1

00 zzzz  00 zzzz 
   
      
 
      












 
21
000000 112
1
CC
zzzzzz
zdzf
zzzzzz
zdzf
i
zf

   
   
    zdzfzz
zzizz
zdzf
zz
i
n
n C
n
n C
n
n





   






0
01
00
1
0
0
21
1
2
1
2
1

   



n
n
n zzazf 0

where
Here C may be any contour with the annular region
r < |z-z0| < R encircling z0 once in a counterclockwise sense.
Laurent Series need not to come from evaluation of
contour integrals. Other techniques such as ordinary series
expansion may provide the coefficients.
Numerous examples of Laurent series appear in the next chapter.
 
  



C
nn
zz
zdzf
i
a 1
0
2
1


 




0
222
1
m
mnimn
i
n
er
drie
i
a 



 
  












0
21 2
1
1
1
2
1
m
n
m
nn
z
zd
z
izz
zd
zi
a

     1
1zzzf






0
1,22
2
1
m
mni
i








1-nfor0
-1nfor1
an
  



 1
32
1
1
1
1
n
n
zzzz
zzz

The Laurent expansion becomes
Example:
(1) Find Taylor expansion ln(1+z) at point z
(2) find Laurent series of the function
If we employ the polar form





1
1
)1()1ln(
n
n
n
n
z
z

• Theorem
Suppose that a function f is analytic throughout an annular
domain R1< |z − z0| < R2, centered at z0 , and let C denote any
positively oriented simple closed contour around z0 and lying in
that domain. Then, at each point in the domain, f (z) has the
series representation
Laurent Series
0 1 0 2
0 1 0
( ) ( ) ,( | | )
( )
n n
n n
n n
b
f z a z z R z z R
z z
 
 
     

 
1
0
1 ( )
,( 0,1,2,...)
2 ( )
n n
C
f z dz
a n
i z z 
 

1
0
1 ( )
,( 1,2,...)
2 ( )
n n
C
f z dz
b n
i z z  
 


• Theorem (Cont’)
Laurent Series
0 1 0 2( ) ( ) ,( | | )n
n
n
f z c z z R z z R


    
0 1 0 2
0 1 0
( ) ( ) ,( | | )
( )
n n
n n
n n
b
f z a z z R z z R
z z
 
 
     

 
1
0
1 ( )
,( 0,1,2,...)
2 ( )
n n
C
f z dz
a n
i z z 
 

1
0
1 ( )
,( 1,2,...)
2 ( )
n n
C
f z dz
b n
i z z  
 

1
0
1 ( )
,( 0, 1, 2,...)
2 ( )
n n
C
f z dz
c n
i z z 
   

1 1
0
0
( )
( )
nn
nn
n n
b
b z z
z z
 


 
 

 
, 1
, 0
n
n
n
b n
c
a n
  
 


• Laurent’s Theorem
If f is analytic throughout the disk |z-z0|<R2,
Laurent Series
0
0
( ) ( )n
n
n
f z a z z


 
1
01
0
1 ( ) 1
( ) ( ) ,( 1,2,...)
2 ( ) 2
n
n n
C C
f z dz
b z z f z dz n
i z z i 

 
   
 
Analytic in the region |z-z0|<R2
0,( 1,2,...)nb n 
( )
0
1
0
( )1 ( )
,( 0,1,2,...)
2 ( ) !
n
n n
C
f zf z dz
a n
i z z n 
  

reduces to Taylor
Series about z0
0 1 0 2
0 1 0
( ) ( ) ,( | | )
( )
n n
n n
n n
b
f z a z z R z z R
z z
 
 
     

 

• Example 1
Replacing z by 1/z in the Maclaurin series expansion
We have the Laurent series representation
Examples
2 3
0
1 ...(| | )
! 1! 2! 3!
n
z
n
z z z z
e z
n


       
1/
2 3
0
1 1 1 1
1 ...(0 | | )
! 1! 2! 3!
z
n
n
e z
n z z z z


        
There is no positive powers of z, and all coefficients of the positive powers are zeros.
1
1 ( )
,( 1,2,...)
2 ( 0)
n n
C
f z dz
b n
i z  
 

1/
1/
1 1 1
1 1
1
2 ( 0) 2
z
z
C C
e dz
b e dz
i z i  
  
 
1/
2z
C
e dz i
where c is any positively oriented simple closed
contours around the origin

• Example 2
The function f(z)=1/(z-i)2 is already in the form of a
Laurent series, where z0=i,. That is
where c-2=1 and all of the other coefficients are zero.
Examples
2
1
( ) ,(0 | | )
( )
n
n
n
c z i z i
z i


     


3
0
1
,( 0, 1, 2,...)
2 ( )
n n
C
dz
c n
i z z 
   

3
0, 2
2 , 2( )n
C
ndz
i nz i 
 
 
  

where c is any positively oriented simple contour
around the point z0=i

Examples
Consider the following function
1 1 1
( )
( 1)( 2) 1 2
f z
z z z z

  
   
which has the two singular points z=1 and z=2, is analytic in the domains
1 :| | 1D z 
3 : 2 | |D z  
2 :1 | | 2D z 

• Example 3
The representation in D1 is Maclaurin series.
Examples
1 1 1 1 1
( )
1 2 1 2 1 ( / 2)
f z
z z z z
     
   
1
1
0 0 0
( ) (2 1) ,(| | 1)
2
n
n n n
n
n n n
z
f z z z z
  
 

  
       
where |z|<1 and |z/2|<1

• Example 4
Because 1<|z|<2 when z is a point in D2, we know
Examples
1 1 1 1 1 1
( )
1 2 1 (1/ ) 2 1 ( / 2)
f z
z z z z z
     
   
where |1/z|<1 and |z/2|<1
1 1 1
0 0 1 0
1 1
( ) ,(1 | | 2)
2 2
n n
n n n n
n n n n
z z
f z z
z z
   
  
   
        

• Theorem 1
If a power series
converges when z = z1 (z1 ≠ z0), then it is absolutely
convergent at each point z in the open disk |z − z0| < R1
where R1 = |z1 − z0|
Some Useful Theorems
0
0
( )n
n
n
a z z




• Theorem
Suppose that a function f is analytic throughout a disk
|z − z0| < R0, centered at z0 and with radius R0. Then f (z)
has the power series representation
Taylor Series
0 0 0
0
( ) ( ) ,(| | )n
n
n
f z a z z z z R


   
( )
0( )
,( 0,1,2,...)
!
n
n
f z
a n
n
 
That is, series converges to f (z) when z
lies in the stated open disk.
1
0
1 ( )
2 ( )
n n
C
f z dz
a
i z z 

 Refer to pp.167

Proof the Taylor’s Theorem
( )
0 0
0
(0)
( ) ,(| | )
!
n
n
n
f
f z z z z R
n


  
Proof:
Let C0 denote and positively oriented circle |z|=r0, where r<r0<R0
Since f is analytic inside and on the circle C0 and since the
point z is interior to C0, the Cauchy integral formula holds
0
0
1 ( )
( ) , ,| |
2 C
f s ds
f z z z R
i s z
  

1 1 1 1 1
, ( / ),| | 1
1 ( / ) 1
   
  
w z s w
s z s z s s w

1
1
0
1 1 1
( )
N
n N
n N
n
z z
s z s s z s



 
 

0
1 ( )
( )
2 C
f s ds
f z
i s z


0 0
1
1
0
1 ( ) 1 ( )
( )
2 2 ( )
N
n N
n N
n C C
f s ds f s ds
f z z z
i s i s z s 



 

  
( )
(0)
!
n
f
n
Refer to pp.167
0
( )1
0
(0) ( )
( )
! 2 ( )
n NN
n
N
n C
f z f s ds
f z z
n i s z s


 

 
ρN

0
( )
lim lim 0
2 ( )
N
N NN N
C
z f s ds
i s z s

 
 

( ) ( ) ( )1
0 0 0
(0) (0) (0)
( ) lim( ) 0
! ! !
n n nN
n n n
N
N
n n n
f f f
f z z z z
n n n

  

  
      
When
0
0
0 0
( ) | |
| | | | 2
2 ( ) 2 ( )
N N
N N N
C
z f s ds r M
r
i s z s r r r
 
 
 
 
Where M denotes the maximum value of |f(s)| on C0
0
0 0
| | ( )N
N
Mr r
r r r
 

lim 0N
N



0
( ) 1
r
r


Example
expand f(z) into a series involving powers of z.
We can not find a Maclaurin series for f(z) since it is not analytic at
z=0. But we do know that expansion
Hence, when 0<|z|<1
Examples
2 2
3 5 3 2 3 2
1 2 1 2(1 ) 1 1 1
( ) (2 )
1 1
z z
f z
z z z z z z
  
   
  
2 4 6 8
2
1
1 ...(| | 1)
1
z z z z z
z
      

2 4 6 8 3 5
3 3
1 1 1
( ) (2 1 ...) ...f z z z z z z z z
z z z
            
Negative powers

Residue theorem
Calculus of residues
Functions of a Complex Variable
Suppose an analytic function f (z) has an isolated singularity at z0. Consider a contour
integral enclosing z0 .
z0
)(sRe22)(
1,2)ln(
1,0
1
)(
)(
)()()(
01
1
'
'01
'
'
1
0
0
00
zfiiadzzf
niazza
n
n
zz
a
dzzza
dzzzadzzzadzzf
C
z
z
z
z
n
n
C
n
n
n
C
n
n
C
n
n
n
C
























  
The coefficient a-1=Res f (z0) in the Laurent expansion is called the residue of f (z) at z = z0.
If the contour encloses multiple isolated
singularities, we have the residue theorem:
 
n
n
C
zfidzzf )(sRe2)( 
z0 z1
Contour integral =2i ×Sum of the residues
at the enclosed singular points

Residue formula:
To find a residue, we need to do the Laurent expansion and pick up the coefficient a-1.
However, in many cases we have a useful residue formula
 
 
 
 )()(lim
)!1(
1
)(sRe
)!1())(2()1)((lim)(lim
)(lim
)!1(
1
)()(lim
)!1(
1
:Proof
.)()(lim)(sRe
,polesimpleaforly,Particular
)()(lim
)!1(
1
)(sRe
,orderofpoleaFor
01
1
01
1
1
1
001
1
01
1
01
1
00
01
1
0
0
00
00
0
0
zfzz
dz
d
m
zfa
mazznmnmnazza
dz
d
zza
dz
d
m
zfzz
dz
d
m
zfzzzf
zfzz
dz
d
m
zf
m
m
m
m
zz
n
n
n
zz
mn
mn
nm
m
zz
mn
mn
nm
m
zz
m
m
m
zz
zz
m
m
m
zz











































 
 
  .0,)()(lim
!
1
:tscoefficientheallfindway toaisethat therprovedactuallyWe
.)()(lim
)!1(
1
usgives1upPick.Also
.)()(lim
!
1
,)()()(
expansionTaylorbyanalytic,is)()(Because
)()()(
)()(
:#2MethodProof
0
01
1
1
00
0
0
0
00
0
0
0
0

























kzfzz
dz
d
k
a
a
zfzz
dz
d
m
amkab
zfzz
dz
d
k
bzzbzfzz
zfzz
zzazfzz
zzazf
m
k
k
zz
mk
m
m
m
zz
mkk
m
k
k
zz
k
k
k
k
m
m
mn
mn
n
m
n
mn
n

Cauchy’s integral theorem and Cauchy’s integral formula revisited:
(in the view of the residue theorem):
   
     
 
 
.
!
)()(
)!11(
1
lim
isatresidueitsformula,residuethetoAccording
1.orderofpoleaisIt.
)(')()(
)'3
!
)(
22
)(
)(
)(
)3
)(2
)(
)('
)()(
)2
0)(Res2)()1
))((')()()(:functionAnalytic
0
)(
1
0
1
01)1(
1)1(
0
0
0
1
0
0
1
0
0
)(
1
00
1
01
0
0
0
0
0
0
0
0
000
0
0
0 n
zf
zz
zf
zz
dz
d
n
zz
n
zz
zf
zz
zf
zz
zf
n
zf
iiadz
zz
zf
zza
zz
zf
zifdz
zz
zf
zf
zz
zf
zz
zf
zfidzzf
zzzfzfzzazf
n
n
n
n
n
zz
nnn
n
n
C n
m
nm
mn
C
C
m
m
m



















































Evaluation of definite integrals -1

 
 
 
 
 
      2222
2
22
2
22
2
22
2
0
22
0
2
2
2
2
2
0
111
2
111
2
1
,
111
1
2
11
)1(1
)(
1111
)(Res)0(Res
.
)(
1
))((
1
lim)(Res
.
1
))((
1
lim)0(Res
circle.theofoutiscircle,in theis||||,1||
.1101/2,0poles,simple3haveWe
)1/2(
11
2
111
2//11
2//1
1.||andrealis,
sin1
sin
Example
aa
a
aa
a
i
ia
I
aa
a
a
a
i
a
a
izzz
zz
zz
z
zz
zff
zzz
z
zzzzz
z
zzzf
zzzzzzz
z
zf
zzzzzz
a
a
i
zaizzz
dz
aizzz
z
ia
dz
aizazz
z
iiz
dz
izza
izz
I
aa
a
d
I
zz
z
CCC





















































































C
r=1
z+
z-
z0

Evaluation of definite integrals -2
II. Integrals along the whole real axis:



dxxf )(
Assumption 1: f (z) is analytic in the upper or lower half of the complex plane, except
isolated finite number of poles.
∩
R
Condition for closure on a semicircular path:
   






 



  dzzfdzzfdzzfdzzfdzzfdxxf
RCR
R
RR
)(lim)(lim)()()(lim)(
  .0,
1
~)(lim0lim)(lim
)(lim)(lim)(lim
1max
0
00









 
  
z
zfRfRdeRf
deiReRfdeiReRfdzzf
RR
i
R
ii
R
ii
RR
Assumption 2: when |z|, | f (z)| goes to zero faster than 1/|z|.
Then, plane.halfupperon the)(ofesiduesR2)(lim)( zfidzzfdxxf
CR
 





 
.arctan
1
Or
.
))((
1
lim2)(Res2
planehalfupperon the
1
1
ofesiduesR2
1
:1Example
2
2
2



























x
x
dx
iziz
iziifi
z
iI
x
dx
I
iz
 
 
  .
2
'
)()(
1
lim2)(Res2
planehalfupperon the
1
ofesiduesR2
.0,
:2Example
322
2
222
222
aaizaiz
iaziiafi
az
iI
a
ax
dx
I
aiz






















MOMENTS, SKEWNESS, AND
KURTOSIS

Moment Ratios
2
3 4
1 23 2
2 2
,
 
 
 
 
2
3 4
1 23 2
2 2
,
m m
b b
m m
 

Skewness
A distribution in which the values equidistant from the mean have equal
frequencies and is called Symmetric Distribution.
Any departure from symmetry is called skewness.
In a perfectly symmetric distribution, Mean=Median=Mode and the two
tails of the distribution are equal in length from the mean. These values are
pulled apart when the distribution departs from symmetry and consequently
one tail become longer than the other.
If right tail is longer than the left tail then the distribution is said to have
positive skewness. In this case, Mean>Median>Mode
If left tail is longer than the right tail then the distribution is said to have
negative skewness. In this case, Mean<Median<Mode

Kurtosis
For a normal distribution, kurtosis is equal to 3.
When is greater than 3, the curve is more sharply peaked and has narrower
tails than the normal curve and is said to be leptokurtic.
When it is less than 3, the curve has a flatter top and relatively wider tails
than the normal curve and is said to be platykurtic.
4
4
2
1 1
4
4
2
1 1
1 1
,
1 1
,
n n
i
i i
n n
i
i i
x
kurt z for populationdata
n n
x x
kurt b z for sampledata
n n s


 
 
 
    
 
 
    
 
 
 

Curve Fitting and Correlation
This will be concerned primarily with two
separate but closely interrelated processes:
(1) the fitting of experimental data to
mathematical forms that describe their
behavior and
(2) the correlation between different
experimental data to assess how closely
different variables are interdependent.

•The fitting of experimental data to a
mathematical equation is called regression.
Regression may be characterized by different
adjectives according to the mathematical form
being used for the fit and the number of
variables. For example, linear regression
involves using a straight-line or linear equation
for the fit. As another example, Multiple
regression involves a function of more than one
independent variable.

Linear Regression
•Assume n points, with each point having values
of both an independent variable x and a
dependent variable y.
1 2 3The values of are , , ,...., .nx x x x x
1 2 3The values of are , , ,...., .ny y y y y
A best-fitting straight line equation
will have the form
1 0y a x a 

Preliminary Computations
0
1
sample mean of the values
n
k
k
x x x
n 
  
0
1
sample mean of the values
n
k
k
y y y
n 
  
2 2
1
1
sample mean-square of the values
n
k
k
x x x
n 
  
1
1
sample mean of the product
n
k k
k
xy xy x y
n 
  

Best-Fitting Straight Line
    
   
1 22
xy x y
a
x x



     
   
2
0 22
x y x xy
a
x x



0 1Alternately, a y a x 
1 0y a x a 

Example-1. Find best fitting straight
line equation for the data shown
below.
x 0 1 2 3 4 5 6 7 8 9
y 4.00 6.10 8.30 9.90 12.40 14.30 15.70 17.40 19.80 22.30
10
1
1 0 1 2 3 4 5 6 7 8 9 45
4.50
10 10 10
k
k
x x

        
   
10
1
1 4 6.1 8.3 9.9 12.4 14.3 15.7 17.4 19.8 22.3
10 10
130.2
13.02
10
k
k
y y

        
 
 


Multiple Linear Regression
0 1 1 2 2 ..... m my a a x a x a x    
Assume independent variablesm
1 2, ,..... mx x x
Assume a dependent variable that
is to be considered as a linear function
of the independent variables.
y
m

Multiple Regression
(Continuation)
1
Assume that there are values of each
of the variables. For , we have
k
m x
11 12 13 1, , ,....., kx x x x
Similar terms apply for all other variables.
For the th variable, we havem
1 2 3, , ,.....,m m m mkx x x x

Correlation
corr( , ) ( )x y E xy xy 
Cross-Correlation
 cov( , ) ( )( )
corr( , ) ( )( )
( )( )
x y E x x y y
x y x y
xy x y
  
 
 
Covariance

Correlation Coefficient
 ( )( )
( , )
cov( , )
cov( , )cov( , )
x y
E x x y y
C x y
x y
x x y y
 
 



Implications of Correlation Coefficient
• 1. If C(x, y) = 1, the two variables are totally
correlated in a positive sense.
• 2. If C(x, y) = -1 , the two variables are totally
correlated in a negative sense.
• 3. If C(x, y) = 0, the two variables are said to
be uncorrelated.

Binomial Distribution and
Applications

Binomial Probability Distribution
A binomial random variable X is defined to the number
of “successes” in n independent trials where the
P(“success”) = p is constant.
Notation: X ~ BIN(n,p)
In the definition above notice the following conditions
need to be satisfied for a binomial experiment:
1. There is a fixed number of n trials carried out.
2. The outcome of a given trial is either a “success”
or “failure”.
3. The probability of success (p) remains constant
from trial to trial.
4. The trials are independent, the outcome of a trial is
not affected by the outcome of any other trial.

Binomial Distribution
• If X ~ BIN(n, p), then
• where
.,...,1,0)1(
)!(!
!
)1()( nxpp
xnx
n
pp
x
n
xXP xnxxnx








 
psuccessP
nx
nnnn








)"("
trials.insuccesses""
obtaintowaysofnumberthex"choosen"
x
n
11!and10!also,1...)2()1(!

• E.g. when n = 3 and p = .50 there are 8 possible
equally likely outcomes (e.g. flipping a coin)
SSS SSF SFS FSS SFF FSF FFS FFF
X=3 X=2 X=2 X=2 X=1 X=1 X=1 X=0
P(X=3)=1/8, P(X=2)=3/8, P(X=1)=3/8, P(X=0)=1/8
• Now let’s use binomial probability formula instead…
.,...,1,0)1(
)!(!
!
)1()( nxpp
xnx
n
pp
x
n
xXP xnxxnx








 

• E.g. when n = 3, p = .50 find P(X = 2)
.,...,1,0)1(
)!(!
!
)1()( nxpp
xnx
n
pp
x
n
xXP xnxxnx








 
8
3or375.)5)(.5(.3)5(.5.
2
3
)2(
ways3
1)12(
123
!1!2
!3
)!23(!2
!3
2
3
12232



















XP
SSF
SFS
FSS

The Poisson Distribution
The Poisson distribution is defined by:
!
)(
x
e
xf
x 
 

Where f(x) is the probability of x occurrences in an interval
 is the expected value or mean value of occurrences within
an interval
e is the natural logarithm. e = 2.71828

Properties of the Poisson Distribution
1. The probability of occurrences is the same for any
two intervals of equal length.
2. The occurrence or nonoccurrence of an event in one
interval is independent of an occurrence on
nonoccurrence of an event in any other interval

Problem
a. Write the appropriate Poisson distribution
b. What is the average number of occurrences in three time periods?
c. Write the appropriate Poisson function to determine the probability
of x occurrences in three time periods.
d. Compute the probability of two occurrences in one time period.
e. Compute the probability of six occurrences in three time periods.
f. Compute the probability of five occurrences in two time periods.
Consider a Poisson probability distribution with an average
number of occurrences of two per period.

Problem
!
2
)(
2
X
e
xf
x 

6
!
6
)(
6
X
e
xf
x 

27067.
2
5413.
!2
2
)2(
22


e
f
(a)
(b)
(c)
(d)

Hypergeometric Distribution
rx
n
N
xn
rN
x
r
xf 




















 0allfor)(
Where
n = the number of trials.
N = number of elements in the population
r = number of elements in the population labeled a success

Parametric and Nonparametric Tests
It introduces two non-parametric hypothesis
tests using the chi-square statistic: the chi-
square test for goodness of fit and the chi-
square test for independence.

(cont.)
• The term "non-parametric" refers to the fact that the
chi-square tests do not require assumptions about
population parameters nor do they test hypotheses
about population parameters.
• Previous examples of hypothesis tests, such as the t
tests and analysis of variance, are parametric tests
and they do include assumptions about parameters
and hypotheses about parameters.

(cont.)
• The most obvious difference between the
chi-square tests and the other hypothesis
tests we have considered (t and ANOVA) is the
nature of the data.
• For chi-square, the data are frequencies rather
than numerical scores.

The Chi-Square Test for Goodness-of-Fit
• The chi-square test for goodness-of-fit uses
frequency data from a sample to test hypotheses
about the shape or proportions of a population.
• Each individual in the sample is classified into one
category on the scale of measurement.
• The data, called observed frequencies, simply count
how many individuals from the sample are in each
category.

The Chi-Square Test for Goodness-of-Fit
(cont.)
• The null hypothesis specifies the proportion of
the population that should be in each
category.
• The proportions from the null hypothesis are
used to compute expected frequencies that
describe how the sample would appear if it
were in perfect agreement with the null
hypothesis.

The Chi-Square Test for Independence
• The second chi-square test, the chi-square
test for independence, can be used and
interpreted in two different ways:
1. Testing hypotheses about the
relationship between two variables in a
population, or
2. Testing hypotheses about
differences between proportions for two
or more populations.

(cont.)
• Although the two versions of the test for
independence appear to be different, they are
equivalent and they are interchangeable.
• The first version of the test emphasizes the
relationship between chi-square and a
correlation, because both procedures examine
the relationship between two variables.

(cont.)
• The second version of the test emphasizes the
relationship between chi-square and an
independent-measures t test (or ANOVA)
because both tests use data from two (or
more) samples to test hypotheses about the
difference between two (or more)
populations.

(cont.)
• The first version of the chi-square test for
independence views the data as one sample in
which each individual is classified on two
different variables.
• The data are usually presented in a matrix
with the categories for one variable defining
the rows and the categories of the second
variable defining the columns.

(cont.)
• The data, called observed frequencies, simply
show how many individuals from the sample
are in each cell of the matrix.
• The null hypothesis for this test states that
there is no relationship between the two
variables; that is, the two variables are
independent.

(cont.)
• The second version of the test for independence
views the data as two (or more) separate samples
representing the different populations being
compared.
• The same variable is measured for each sample by
classifying individual subjects into categories of the
variable.
• The data are presented in a matrix with the different
samples defining the rows and the categories of the
variable defining the columns..

(cont.)
• The data, again called observed frequencies,
show how many individuals are in each cell of
the matrix.
• The null hypothesis for this test states that the
proportions (the distribution across
categories) are the same for all of the
populations

(cont.)
• Both chi-square tests use the same statistic. The
calculation of the chi-square statistic requires two
steps:
1. The null hypothesis is used to construct an idealized
sample distribution of expected frequencies that
describes how the sample would look if the data
were in perfect agreement with the null hypothesis.

(cont.)
For the goodness of fit test, the expected frequency for each
category is obtained by
expected frequency = fe = pn
(p is the proportion from the null hypothesis and n is the size
of the sample)
For the test for independence, the expected frequency for each
cell in the matrix is obtained by
(row total)(column total)
expected frequency = fe = ─────────────────
n

(cont.)
2. A chi-square statistic is computed to measure the
amount of discrepancy between the ideal sample
(expected frequencies from H0) and the actual
sample data (the observed frequencies = fo).
A large discrepancy results in a large value for chi-
square and indicates that the data do not fit the null
hypothesis and the hypothesis should be rejected.

(cont.)
The calculation of chi-square is the same for all chi-
square tests:
(fo – fe)2
chi-square = χ2 = Σ ─────
fe
The fact that chi-square tests do not require scores
from an interval or ratio scale makes these tests a
valuable alternative to the t tests, ANOVA, or
correlation, because they can be used with data
measured on a nominal or an ordinal scale.

Measuring Effect Size for the Chi-Square
Test for Independence
• When both variables in the chi-square test for
independence consist of exactly two
categories (the data form a 2x2 matrix), it is
possible to re-code the categories as 0 and 1
for each variable and then compute a
correlation known as a phi-coefficient that
measures the strength of the relationship.

Measuring Effect Size for the Chi-Square Test
for Independence (cont.)
• The value of the phi-coefficient, or the
squared value which is equivalent to an r2, is
used to measure the effect size.
• When there are more than two categories for
one (or both) of the variables, then you can
measure effect size using a modified version
of the phi-coefficient known as Cramér=s V.
• The value of V is evaluated much the same as
a correlation.

The t-test
Inferences about Population Means

Questions
• What is the main use of the t-test?
• How is the distribution of t related to the unit
normal?
• When would we use a t-test instead of a z-test? Why
might we prefer one to the other?
• What are the chief varieties or forms of the t-test?
• What is the standard error of the difference between
means? What are the factors that influence its size?

Background
• The t-test is used to test hypotheses about
means when the population variance is
unknown (the usual case). Closely related to
z, the unit normal.
• Developed by Gossett for the quality control
of beer.
• Comes in 3 varieties:
• Single sample, independent samples, and
dependent samples.

What kind of t is it?
• Single sample t – we have only 1 group; want to test
against a hypothetical mean.
• Independent samples t – we have 2 means, 2 groups;
no relation between groups, e.g., people randomly
assigned to a single group.
• Dependent t – we have two means. Either same
people in both groups, or people are related, e.g.,
husband-wife, left hand-right hand, hospital patient
and visitor.

Single-sample z test
• For large samples (N>100) can use z to test
hypotheses about means.
• Suppose
• Then
• If
M
M
est
X
z


.
)( 

N
N
XX
N
s
est X
M
1
)(
.
2





200;5;10:;10: 10  NsHH X
35.
14.14
5
200
5
. 
N
s
est X
M
05.96.183.2;83.2
35.
)1011(
11 

 pzX

The t Distribution
We use t when the population variance is unknown (the usual case) and
sample size is small (N<100, the usual case). If you use a stat package for
testing hypotheses about means, you will use t.
The t distribution is a short, fat relative of the normal. The shape of t depends
on its df. As N becomes infinitely large, t becomes normal.

Degrees of Freedom
For the t distribution, degrees of freedom are always a simple function of the
sample size, e.g., (N-1).
One way of explaining df is that if we know the total or mean, and all but one
score, the last (N-1) score is not free to vary. It is fixed by the other scores.
4+3+2+X = 10. X=1.

Single-sample t-test
With a small sample size, we compute the same numbers as we did for z,
but we compare them to the t distribution instead of the z distribution.
25;5;10:;10: 10  NsHH X
1
25
5
. 
N
s
est X
M 1
1
)1011(
11 

 tX
064.2)24,05(. t 1<2.064, n.s.
Interval =
]064.13,936.8[)1(064.211
ˆ

 MtX 
Interval is about 9 to 13 and contains 10, so n.s.
(c.f. z=1.96)

Difference Between Means (1)
• Most studies have at least 2 groups (e.g., M
vs. F, Exp vs. Control)
• If we want to know diff in population means,
best guess is diff in sample means.
• Unbiased:
• Variance of the Difference:
• Standard Error:
2
2
2
121 )var( MMyy  
212121 )()()(   yEyEyyE
2
2
2
1 MMdiff  

Difference Between Means (2)
• We can estimate the standard error of the
difference between means.
• For large samples, can use z
2
2
2
1 ... MMdiff estestest  
diffest
XX
diffz 
 )()( 2121 

3;100;12
2;100;10
0:;0:
222
111
211210



SDNX
SDNX
HH 
36.
100
13
100
9
100
4
. diffest 
05.;56.5
36.
2
36.
0)1210(


 pzdiff

Independent Samples t (1)
• Looks just like z:
• df=N1-1+N2-1=N1+N2-2
• If SDs are equal, estimate is:
diffest
yy
difft 
 )()( 2121 








21
2
2
2
1
2
11
NNNN
diff 


Pooled variance estimate is weighted average:
)]2/(1/[])1()1[( 21
2
22
2
11
2
 NNsNsN
Pooled Standard Error of the Difference (computed):





 



21
21
21
2
22
2
11
2
)1()1(
.
NN
NN
NN
sNsN
est diff

Independent Samples t (2)





 



21
21
21
2
22
2
11
2
)1()1(
.
NN
NN
NN
sNsN
est diff
diffest
yy
difft 
 )()( 2121 

7;83.5;20
5;7;18
0:;0:
2
2
22
1
2
11
211210



Nsy
Nsy
HH 
47.1
35
12
275
)83.5(6)7(4
. 





diffest 
..;36.1
47.1
2
47.1
0)2018(
sntdiff 




tcrit = t(.05,10)=2.23

Dependent t (1)
Observations come in pairs. Brother, sister, repeated measure.
),cov(2 21
2
2
2
1
2
yyMMdiff  
Problem solved by finding diffs between pairs Di=yi1-yi2.
1
)( 2
2




N
DD
s i
D
N
s
est D
MD .N
D
D i
)(
MDest
DED
t
.
)(
 df=N(pairs)-1

Dependent t (2)
Brother Sister
5 7
7 8
3 3
5y 6y
Diff
2 1
1 0
0 1
1D
58.3/1. MDest 
72.1
58.
1
.
)(



MDest
DED
t

1
1
)( 2





N
DD
sD
2
)( DD 

Assumptions
• The t-test is based on assumptions of
normality and homogeneity of variance.
• You can test for both these (make sure you
learn the SAS methods).
• As long as the samples in each group are large
and nearly equal, the t-test is robust, that is,
still good, even tho assumptions are not met.

Introduction
• Root of a function:
• Root of a function f(x) = a value a such that:
• f(a) = 0

Introduction (cont.)
• Example:
Function: f(x) = x2 - 4
Roots: x = -2, x = 2
Because:
f(-2) = (-2)2 - 4 = 4 - 4 = 0
f(2) = (2)2 - 4 = 4 - 4 = 0

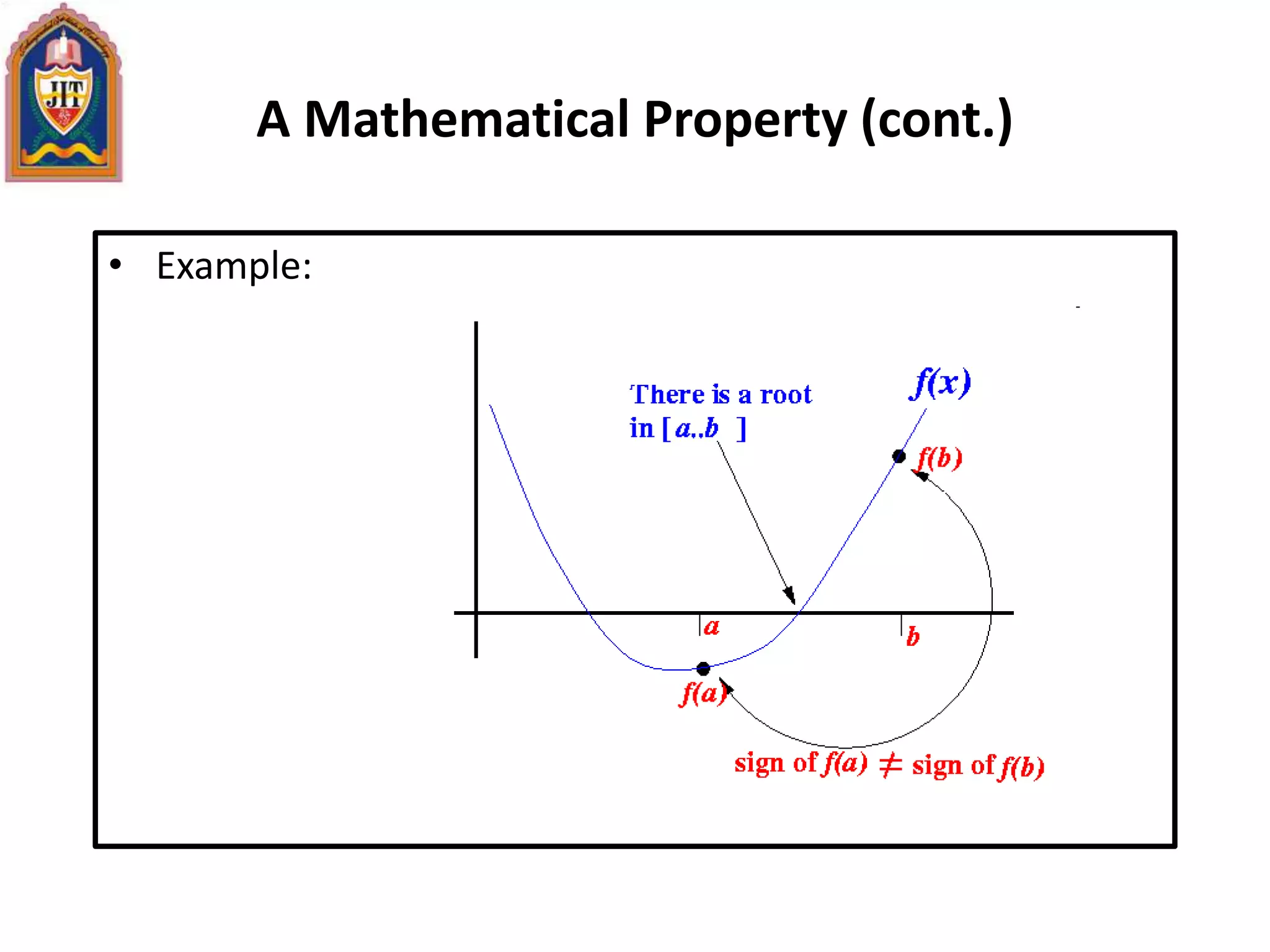
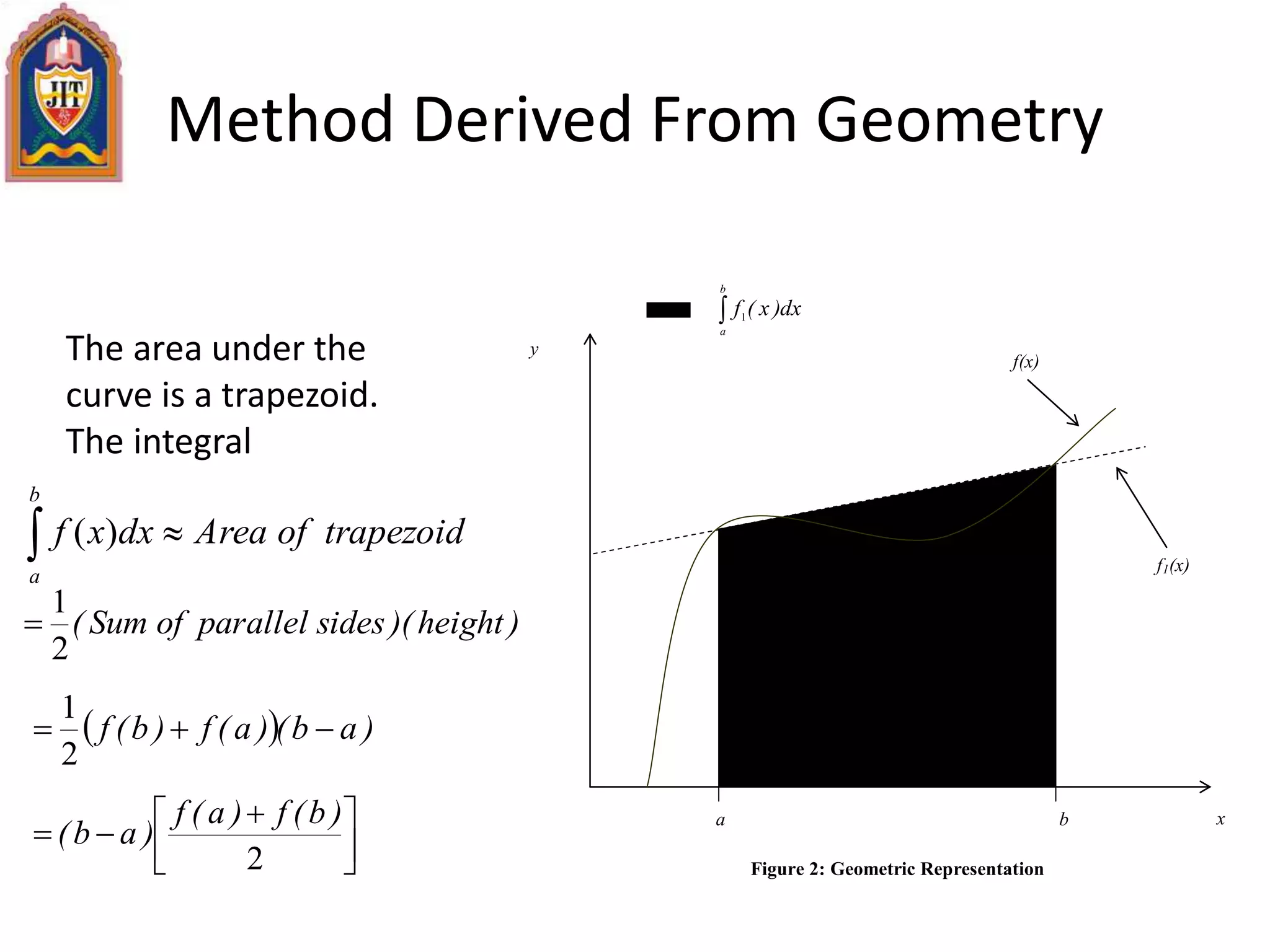
A Mathematical Property
• Well-known Mathematical Property:
• If a function f(x) is continuous on the interval [a..b] and sign of f(a) ≠ sign of
f(b), then
• There is a value c ∈ [a..b] such that: f(c) = 0 I.e., there is
a root c in the interval [a..b]

A Mathematical Property (cont.)
• Example:

The Bisection Method
• The Bisection Method is a successive approximation method
that narrows down an interval that contains a root of the
function f(x)
• The Bisection Method is given an initial interval [a..b] that
contains a root (We can use the property sign of f(a) ≠ sign of
f(b) to find such an initial interval)
• The Bisection Method will cut the interval into 2 halves and
check which half interval contains a root of the function
• The Bisection Method will keep cut the interval in halves until
the resulting interval is extremely small
The root is then approximately equal to any value in the final
(very small) interval.

The Bisection Method (cont.)
• Example:
• Suppose the interval [a..b] is as follows:

• We cut the interval [a..b] in the middle: m = (a+b)/2

• Because sign of f(m) ≠ sign of f(a) , we proceed with the
search in the new interval [a..b]:

We can use this statement to change to the new interval:
b = m;

• In the above example, we have changed the end point b to
obtain a smaller interval that still contains a root
In other cases, we may need to changed the end point b to
obtain a smaller interval that still contains a root

• Here is an example where you have to change the end
point a:
• Initial interval [a..b]:

• After cutting the interval in half, the root is contained in the
right-half, so we have to change the end point a:

• Rough description (pseudo code) of the Bisection Method:
Given: interval [a..b] such that: sign of f(a) ≠ sign of f(b)
repeat (until the interval [a..b] is "very small")
{
a+b
m = -----; // m = midpoint of interval [a..b]
2
if ( sign of f(m) ≠ sign of f(b) )
{
use interval [m..b] in the next iteration

(i.e.: replace a with m)
}
else
{
use interval [a..m] in the next iteration
(i.e.: replace b with m)
}
}
Approximate root = (a+b)/2; (any point between [a..b] will do
because the interval [a..b] is very small)

• Structure Diagram of the Bisection Algorithm:

• Example execution:
• We will use a simple function to illustrate the execution of the Bisection
Method
• Function used:
Roots: √3 = 1.7320508... and −√3 = −1.7320508...
f(x) = x2 - 3

• We will use the starting interval [0..4] since:
The interval [0..4] contains a root because: sign of f(0) ≠
sign of f(4)
• f(0) = 02 − 3 = −3
• f(4) = 42 − 3 = 13

Regula-Falsi Method
Type of Algorithm (Equation Solver)
The Regula-Falsi Method (sometimes called the False Position Method) is a method used
to find a numerical estimate of an equation.
This method attempts to solve an equation of the form f(x)=0. (This is very common in
most numerical analysis applications.) Any equation can be written in this form.
Algorithm Requirements
This algorithm requires a function f(x) and two points a and b for which f(x) is positive for
one of the values and negative for the other. We can write this condition as f(a)f(b)<0.
If the function f(x) is continuous on the interval [a,b] with f(a)f(b)<0, the algorithm will
eventually converge to a solution.
This algorithm can not be implemented to find a tangential root. That is a root that is
tangent to the x-axis and either positive or negative on both side of the root. For example
f(x)=(x-3)2, has a tangential root at x=3.

Regula-Falsi Algorithm
The idea for the Regula-Falsi method is to connect the points (a,f(a)) and (b,f(b)) with a
straight line.
Since linear equations are the simplest equations to solve for find the regula-falsi point
(xrfp) which is the solution to the linear equation connecting the endpoints.
Look at the sign of f(xrfp):
If sign(f(xrfp)) = 0 then end algorithm
else If sign(f(xrfp)) = sign(f(a)) then set a = xrfp
else set b = xrfp
x-axis
a b
f(b)
f(a) actual root
f(x)
xrfp
equation of line:
 ax
ab
afbf
afy 



)()(
)(
solving for xrfp
 
 
 
)()(
)(
)()(
)(
)()(
)(0
afbf
abaf
ax
ax
afbf
abaf
ax
ab
afbf
af
rfp
rfp
rfp











Example
Lets look for a solution to the equation x3-2x-3=0.
We consider the function f(x)=x3-2x-3
On the interval [0,2] the function is negative at 0 and positive at 2. This means that a=0
and b=2 (i.e. f(0)f(2)=(-3)(1)=-3<0, this means we can apply the algorithm).
 
2
3
4
6
31
)2(3
)0()2(
02)0(
0 








ff
f
xrfp
8
21
2
3
)(







 fxf rfp
This is negative and we will make the a =3/2 and
b is the same and apply the same thing to the
interval [3/2,2].
  
 
 
29
54
58
21
2
3
12
3
)2(
2
2
3
8
21
2
1
8
21
2
3
2
3
2
3





 

ff
f
xrfp
267785.0
29
54
)( 





 fxf rfp
This is negative and we will make the a =54/29 and
b is the same and apply the same thing to the
interval [54/29,2].

Stopping Conditions
Aside from lucking out and actually hitting the root, the stopping condition is usually fixed
to be a certain number of iterations or for the Standard Cauchy Error in computing the
Regula-Falsi Point (xrfp) to not change more than a prescribed amount (usually denoted ).

Unit - IV
Interpolation
• Estimation of intermediate values between precise
data points. The most common method is:
• Although there is one and only one nth-order
polynomial that fits n+1 points, there are a variety of
mathematical formats in which this polynomial can be
expressed:
– The Newton polynomial
– The Lagrange polynomial
n
n xaxaxaaxf  2
210)(

Newton’s Divided-Difference Interpolating
Polynomials
Linear Interpolation/
• Is the simplest form of interpolation, connecting two data
points with a straight line.
• f1(x) designates that this is a first-order interpolating
polynomial.
)(
)()(
)()(
)()()()(
0
0
01
01
0
01
0
01
xx
xx
xfxf
xfxf
xx
xfxf
xx
xfxf









Linear-interpolation
formula
Slope and a
finite divided
difference
approximation to
1st derivative

Quadratic Interpolation/
• If three data points are available, the estimate is
improved by introducing some curvature into the line
connecting the points.
• A simple procedure can be used to determine the
values of the coefficients.
))(()()( 1020102 xxxxbxxbbxf 
02
01
01
12
12
22
0
01
11
000
)()()()(
)()(
)(
xx
xx
xfxf
xx
xfxf
bxx
xx
xfxf
bxx
xfbxx












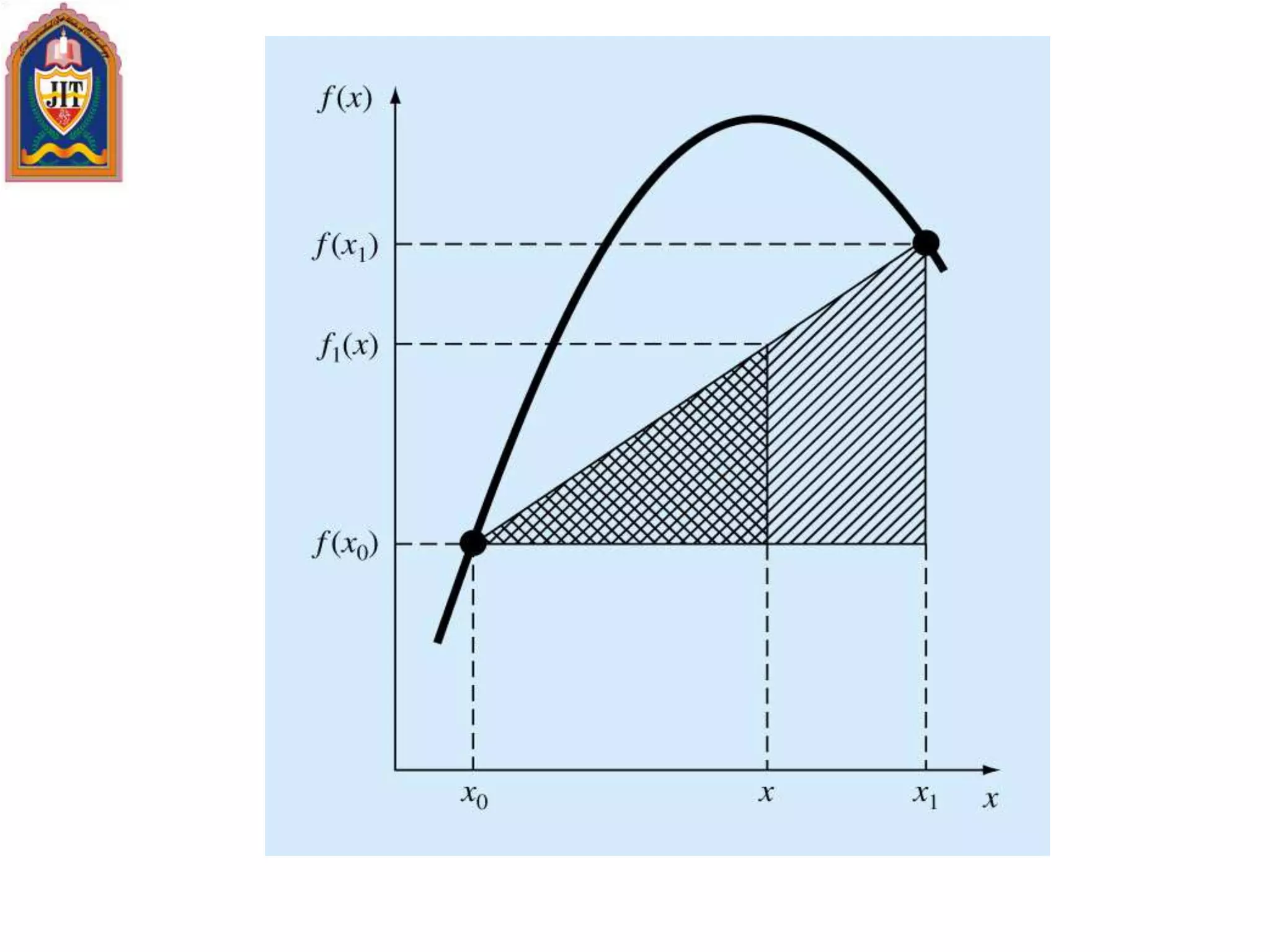
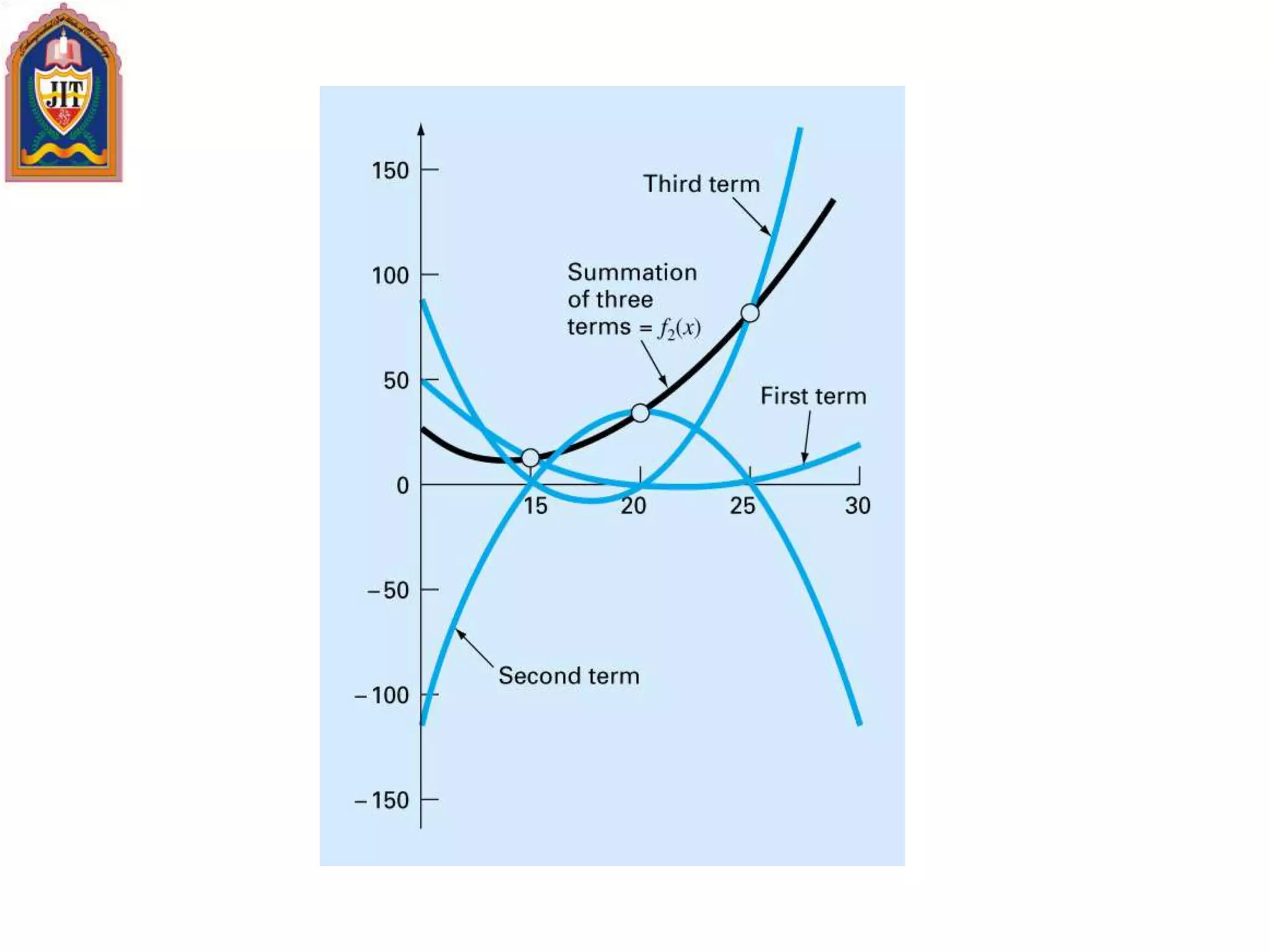
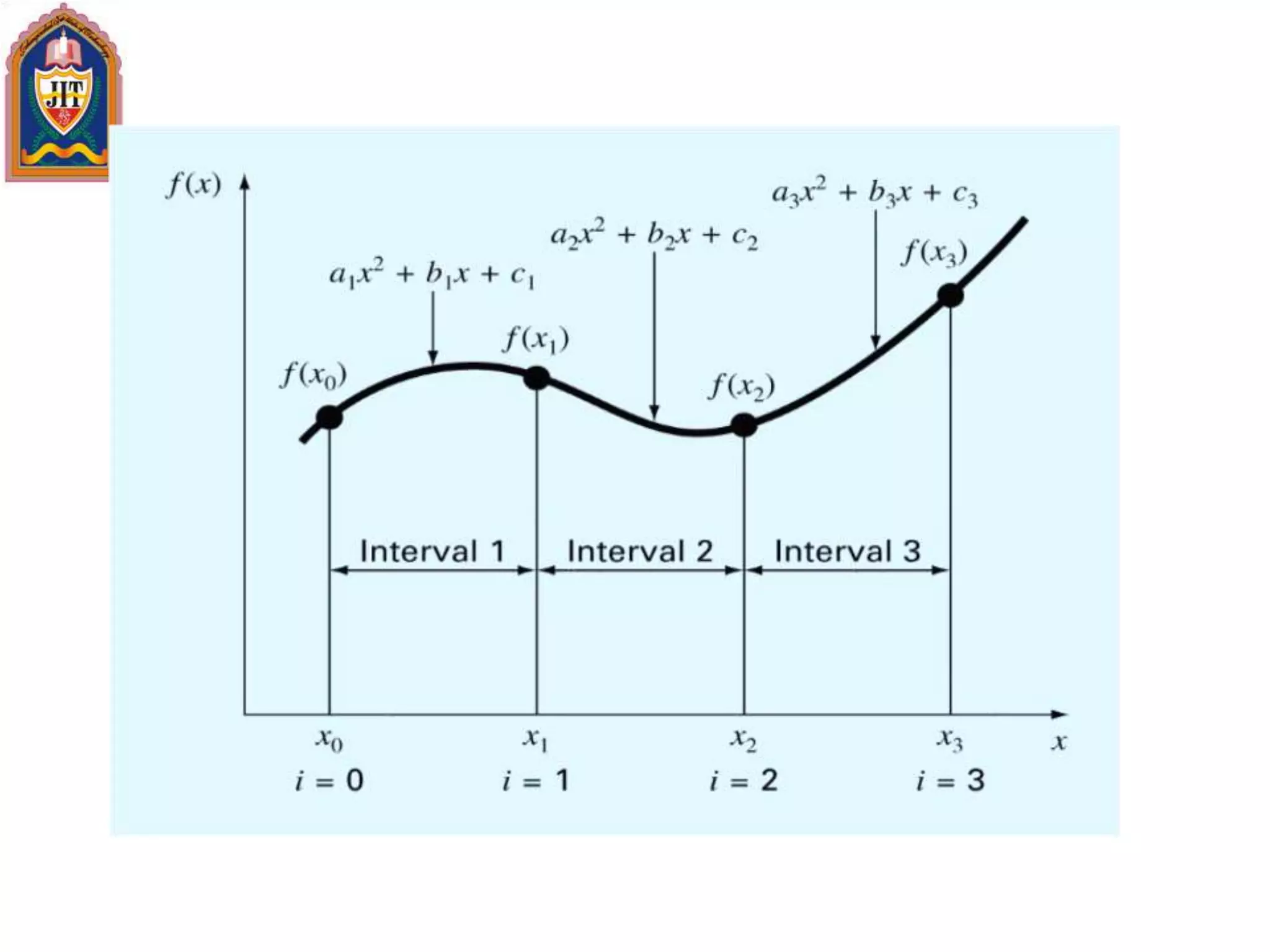
General Form of Newton’s Interpolating Polynomials/
0
02111
011
011
0122
011
00
01110
012100100
],,,[],,,[
],,,,[
],[],[
],,[
)()(
],[
],,,,[
],,[
],[
)(
],,,[)())((
],,[))((],[)()()(
xx
xxxfxxxf
xxxxf
xx
xxfxxf
xxxf
xx
xfxf
xxf
xxxxfb
xxxfb
xxfb
xfb
xxxfxxxxxx
xxxfxxxxxxfxxxfxf
n
nnnn
nn
ki
kjji
kji
ji
ji
ji
nnn
nnn
n

























Bracketed function
evaluations are finite
divided differences

Errors of Newton’s Interpolating Polynomials/
• Structure of interpolating polynomials is similar to the Taylor
series expansion in the sense that finite divided differences are
added sequentially to capture the higher order derivatives.
• For an nth-order interpolating polynomial, an analogous
relationship for the error is:
• For non differentiable functions, if an additional point f(xn+1) is
available, an alternative formula can be used that does not
require prior knowledge of the function:
)())((
)!1(
)(
10
)1(
n
n
n xxxxxx
n
f
R 





)())(](,,,,[ 10011 nnnnn xxxxxxxxxxfR   
 Is somewhere
containing the unknown
and he data

Lagrange Interpolating Polynomials
• The Lagrange interpolating polynomial is simply a
reformulation of the Newton’s polynomial that
avoids the computation of divided differences:









n
ij
j ji
j
i
n
i
iin
xx
xx
xL
xfxLxf
0
0
)(
)()()(

  
  
  
  
  
  
)(
)()()(
)()()(
2
1202
10
1
2101
20
0
2010
21
2
1
01
0
0
10
1
1
xf
xxxx
xxxx
xf
xxxx
xxxx
xf
xxxx
xxxx
xf
xf
xx
xx
xf
xx
xx
xf















•As with Newton’s method, the Lagrange version has an
estimated error of:

 
n
i
innn xxxxxxfR
0
01 )(],,,,[ 

Coefficients of an Interpolating
Polynomial
• Although both the Newton and Lagrange
polynomials are well suited for determining
intermediate values between points, they do not
provide a polynomial in conventional form:
• Since n+1 data points are required to determine n+1
coefficients, simultaneous linear systems of equations
can be used to calculate “a”s.
n
x xaxaxaaxf  2
210)(

n
nnnnn
n
n
n
n
xaxaxaaxf
xaxaxaaxf
xaxaxaaxf







2
210
1
2
121101
0
2
020100
)(
)(
)(
Where “x”s are the knowns and “a”s are the unknowns.

Spline Interpolation
• There are cases where polynomials can lead to
erroneous results because of round off error
and overshoot.
• Alternative approach is to apply lower-order
polynomials to subsets of data points. Such
connecting polynomials are called spline
functions.

NEWTON FORWARD INTERPOLATION ON EQUISPACED POINTS
• Lagrange Interpolation has a number of disadvantages
• The amount of computation required is large
• Interpolation for additional values of requires the same amount of effort
as the first value (i.e. no part of the previous calculation can be used)
• When the number of interpolation points are changed
(increased/decreased), the results of the previous computations can not
be used
• Error estimation is difficult (at least may not be convenient)
• Use Newton Interpolation which is based on developing difference
tables for a given set
of data points

Newton’s Divided Difference Polynomial Method
To illustrate this method, linear and quadratic interpolation is presented first.
Then, the
general form of Newton’s divided difference polynomial method is presented. To
illustrate
the general form, cubic interpolation is shown in Figure

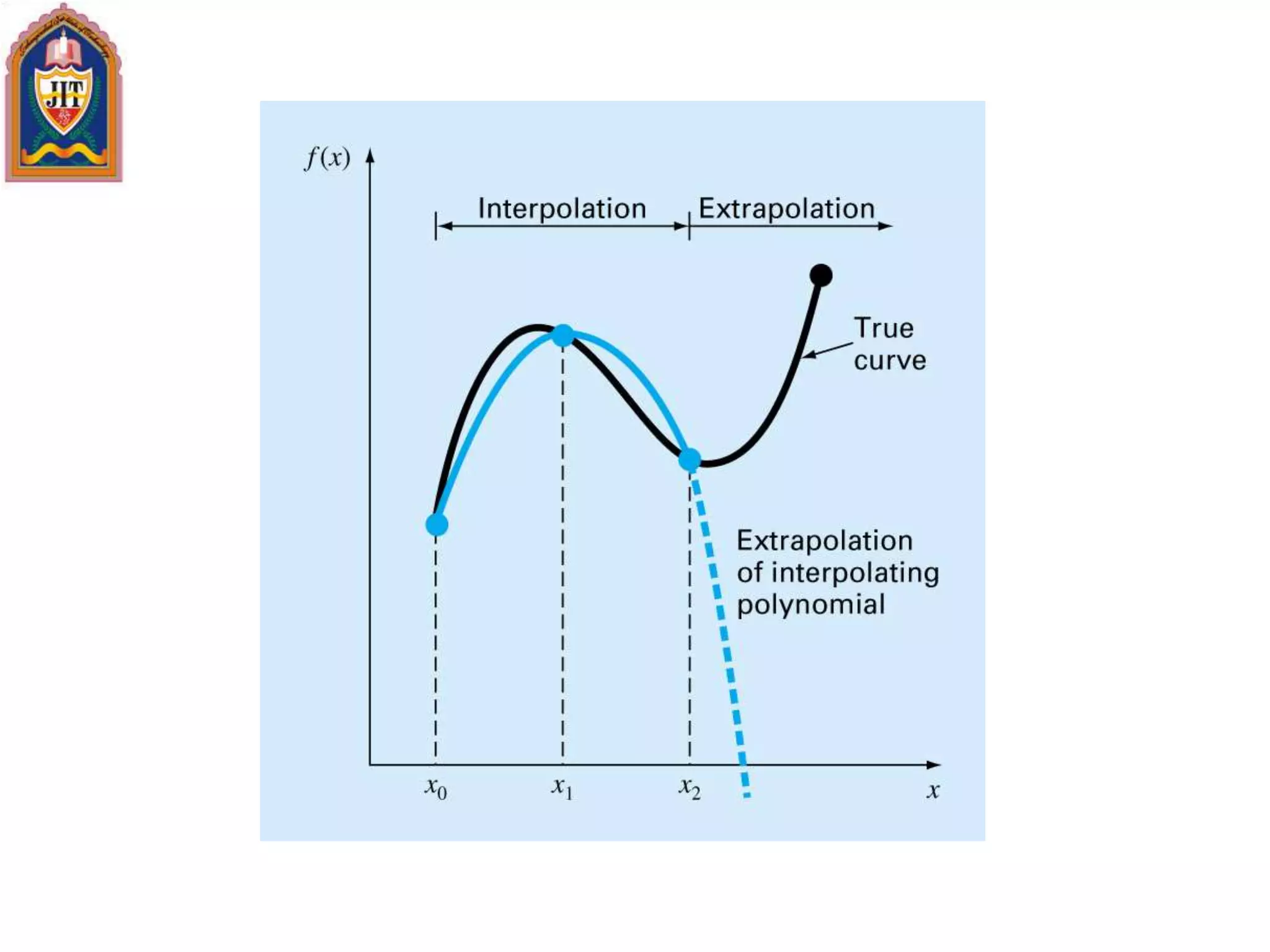
Introduction
Some of most frequently used decompositions are the LU, QR,
Cholesky, Jordan, Spectral decomposition and Singular value
decompositions.
This Lecture covers relevant matrix decompositions, basic
numerical methods, its computation and some of its
applications.
Decompositions provide a numerically stable way to solve
a system of linear equations, as shown already in
[Wampler, 1970], and to invert a matrix. Additionally, they
provide an important tool for analyzing the numerical stability
of a system.

Easy to solve system
Some linear system that can be easily solved
The solution:












nnn ab
ab
ab
/
/
/
222
111


Easy to solve system (Cont.)
Lower triangular matrix:
Solution: This system is solved using forward substitution

Easy to solve system (Cont.)
Upper Triangular Matrix:
Solution: This system is solved using Backward substitution

LU Decomposition
and
Where,













mm
m
m
u
uu
uuu
U




00
0 222
11211













mmmm lll
ll
l
L




21
2221
11
0
00
LUA 
LU decomposition was originally derived as a decomposition of quadratic and
bilinear forms. Lagrange, in the very first paper in his collected works( 1759) derives
the algorithm we call Gaussian elimination. Later Turing introduced the LU
decomposition of a matrix in 1948 that is used to solve the system of linear
equation.
Let A be a m × m with nonsingular square matrix. Then there exists two matrices L
and U such that, where L is a lower triangular matrix and U is an upper triangular
matrix.

A … U (upper triangular)
 U = Ek  E1 A
 A = (E1)1  (Ek)1 U
If each such elementary matrix Ei is a lower triangular matrices,
it can be proved that (E1)1, , (Ek)1 are lower triangular, and
(E1)1  (Ek)1 is a lower triangular matrix.
Let L=(E1)1  (Ek)1 then A=LU.
How to decompose A=LU?







































































































2133
6812
226
102/1
012
001
130
010
001
500
240
226
2133
6812
226
102/1
012
001
1120
240
226
Now,
2133
6812
226
A
U E2 E1 A

Calculation of L and U (cont.)
Now reducing the first column we have














2133
6812
226
A























2133
6812
226
100
010
001

























































































2133
6812
226
102/1
012
001
130
010
001
500
240
226
2133
6812
226
102/1
012
001
1120
240
226
=

If A is a Non singular matrix then for each L (lower triangular matrix) the
upper triangular matrix is unique but an LU decomposition is not unique.
There can be more than one such LU decomposition for a matrix. Such as
Calculation of L and U























































132/1
012
001
130
010
001
102/1
012
001
130
010
001
102/1
012
001
11














2133
6812
226
A










132/1
012
001













500
240
226














2133
6812
226
A










133
0112
006













500
240
6/26/21
Now
Therefore,
=
=LU=
=LU

Calculation of L and U (cont.)
Thus LU decomposition is not unique. Since we compute LU
decomposition by elementary transformation so if we change L
then U will be changed such that A=LU
To find out the unique LU decomposition, it is necessary to
put some restriction on L and U matrices. For example, we can
require the lower triangular matrix L to be a unit one (i.e. set
all the entries of its main diagonal to ones).
LU Decomposition in R:
• library(Matrix)
• x<-matrix(c(3,2,1, 9,3,4,4,2,5 ),ncol=3,nrow=3)
• expand(lu(x))

• Note: there are also generalizations of LU to non-square and singular
matrices, such as rank revealing LU factorization.
• [Pan, C.T. (2000). On the existence and computation of rank revealing LU
factorizations. Linear Algebra and its Applications, 316: 199-222.
• Miranian, L. and Gu, M. (2003). Strong rank revealing LU factorizations.
Linear Algebra and its Applications, 367: 1-16.]
• Uses: The LU decomposition is most commonly used in the solution of
systems of simultaneous linear equations. We can also find determinant
easily by using LU decomposition (Product of the diagonal element of
upper and lower triangular matrix).

Solving system of linear equation
using LU decomposition
Suppose we would like to solve a m×m system AX = b. Then we can find
a LU-decomposition for A, then to solve AX =b, it is enough to solve the
systems
Thus the system LY = b can be solved by the method of forward
substitution and the system UX = Y can be solved by the method of
backward substitution. To illustrate, we give some examples
Consider the given system AX = b, where
and














2133
6812
226
A












17
14
8
b

We have seen A = LU, where
Thus, to solve AX = b, we first solve LY = b by forward substitution
Then
Solving system of linear equation
using LU decomposition











132/1
012
001
L














500
240
226
U
































17
14
8
132/1
012
001
3
2
1
y
y
y























15
2
8
3
2
1
y
y
y
Y

Now, we solve UX =Y by backward substitution
then
Solving system of linear
equation using LU
decomposition



































15
2
8
500
240
226
3
2
1
x
x
x





















3
2
1
3
2
1
x
x
x

QR Decomposition
If A is a m×n matrix with linearly independent columns, then A can be
decomposed as , where Q is a m×n matrix whose columns
form an orthonormal basis for the column space of A and R is an
nonsingular upper triangular matrix.
QRA 

QR-Decomposition
Theorem : If A is a m×n matrix with linearly independent columns, then
A can be decomposed as , where Q is a m×n matrix whose
columns form an orthonormal basis for the column space of A and R is an
nonsingular upper triangular matrix.
Proof: Suppose A=[u1 | u2| . . . | un] and rank (A) = n.
Apply the Gram-Schmidt process to {u1, u2 , . . . ,un} and the
orthogonal vectors v1, v2 , . . . ,vn are
Let for i=1,2,. . ., n. Thus q1, q2 , . . . ,qn form a orthonormal
basis for the column space of A.
QRA 
12
1
1
22
2
2
12
1
1 ,,,



 i
i
iiii
ii v
v
vu
v
v
vu
v
v
vu
uv 
i
i
i
v
v
q 

QR-Decomposition
Now,
i.e.,
Thus ui is orthogonal to qj for j>i;
12
1
1
22
2
2
12
1
1 ,,,



 i
i
iiii
ii v
v
vu
v
v
vu
v
v
vu
vu 
112211 ,,,  iiiiiiii qquqquqquqvu 
},,{},,,{ 221 iiii qqqspanvvvspanu  
112211
223113333
112222
111
,,,
,,
,




nnnnnnnn qquqquqquqvu
qquqquqvu
qquqvu
qvu



Let Q= [q1 q2 . . . qn] , so Q is a m×n matrix whose columns form an
orthonormal basis for the column space of A .
Now,
i.e., A=QR.
Where,
Thus A can be decomposed as A=QR , where R is an upper triangular and
nonsingular matrix.
QR-Decomposition
   

















n
n
n
n
nn
v
quv
ququv
quququv
qqquuuA
0000
,00
,,0
,,,
33
2232
113121
2121






















n
n
n
n
v
quv
ququv
quququv
R
0000
,00
,,0
,,,
33
2232
113121





QR Decomposition
Example: Find the QR decomposition of
















100
011
001
111
A

Applying Gram-Schmidt process of computing QR decomposition
1st Step:
2nd Step:
3rd Step:
Calculation of QR
Decomposition
















0
31
31
31
1
3
1
1
1
111
a
a
q
ar
322112  aqr T



































































0
6/1
32
6/1
ˆ
ˆ
1
32ˆ
0
3/1
3/2
3/1
0
31
31
31
)3/2(
0
1
0
1
ˆ
2
2
2
222
121221122
q
q
q
qr
rqaaqqaq T

4th Step:
5th Step:
6th Step:
Calculation of QR
Decomposition
313113  aqr T
613223  aqr T



































6/2
6/1
0
6/1
ˆ
ˆ
1
2/6ˆ
1
2/1
0
2/1
ˆ
3
3
3
333
223113332231133
q
q
q
qr
qrqraaqqaqqaq TT

Therefore, A=QR
R code for QR Decomposition:
x<-matrix(c(1,2,3, 2,5,4, 3,4,9),ncol=3,nrow=3)
qrstr <- qr(x)
Q<-qr.Q(qrstr)
R<-qr.R(qrstr)
Uses: QR decomposition is widely used in computer codes to find the
eigenvalues of a matrix, to solve linear systems, and to find least squares
approximations.
Calculation of QR
Decomposition









 

































2/600
6/16/20
3/13/23
6/200
6/16/13/1
06/23/1
6/16/13/1
100
011
001
111

Least square solution using QR
Decomposition
The least square solution of b is
Let X=QR. Then
Therefore,
  YXbXX tt

    ZYQRbYQRRRbRRYQRRbR ttttttttt

 11
     
YQRYX
RbRQRbQRbQRQRbXX
ttt
ttttt



Procedure To find out the cholesky decomposition
Suppose
We need to solve
the equation













nnnn
n
n
aaa
aaa
aaa
A




21
22221
11211
  




  








T
L
nn
n
n
L
nnnnnnnn
n
n
l
ll
lll
lll
ll
l
aaa
aaa
aaa
A






































00
00
00
222
12111
21
2221
11
21
22221
11211

Example of Cholesky Decomposition
Suppose
Then Cholesky Decomposition
Now,
2/11
1
2






 


k
s
kskkkk lal












522
2102
224
A












311
031
002
L
For k from 1 to n
For j from k+1 to n
kk
k
s
ksjsjkjk lllal 





 


1
1

R code for Cholesky Decomposition
• x<-matrix(c(4,2,-2, 2,10,2, -2,2,5),ncol=3,nrow=3)
• cl<-chol(x)
• If we Decompose A as LDLT then
and












13/12/1
012/1
001
L











300
090
004
D

Application of Cholesky
Decomposition
Cholesky Decomposition is used to solve the system
of linear equation Ax=b, where A is real symmetric
and positive definite.
In regression analysis it could be used to estimate the
parameter if XTX is positive definite.
In Kernel principal component analysis, Cholesky
decomposition is also used (Weiya Shi; Yue-Fei
Guo; 2010)

Jordan Decomposition
• Let A be any n×n matrix then there exists a nonsingular matrix P and JK(λ)
a k×k matrix form
Such that





















000
010
001
)(kJ















)(000
0)(0
00)(
2
1
1 2
1
rk
k
k
r
J
J
J
APP






where k1+k2+ … + kr =n. Also λi , i=1,2,. . ., r are the characteristic roots
And ki are the algebraic multiplicity of λi ,
Jordan Decomposition is used in Differential equation and time series analysis.

Spectral Decomposition
Let A be a m × m real symmetric matrix. Then
there exists an orthogonal matrix P such that
or , where Λ is a diagonal
matrix.
APPT T
PPA 

Basic Idea on Jacobi method
Convert the system:
into the equivalent system:
• Generate a sequence of approximation
BAx 
dCxx 
dCxx kk
  )1()(
,..., )2()1(
xx
3333132131
2323122121
1313212111
bxaxaxa
bxaxaxa
bxaxaxa



33
3
2
33
32
1
33
31
3
22
2
3
22
23
1
22
21
2
11
1
3
11
13
2
11
12
1
a
b
x
a
a
x
a
a
x
a
b
x
a
a
x
a
a
x
a
b
x
a
a
x
a
a
x




Jacobi iteration method
nnnnnn
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa







2211
22222121
11212111















0
0
2
0
1
0
nx
x
x
x

)(
1 0
1
0
2121
11
1
1 nn xaxab
a
x  
)(
1 0
11
0
22
0
11
1
 nnnnnn
nn
n xaxaxab
a
x 
)(
1 0
2
0
323
0
1212
22
1
2 nn xaxaxab
a
x  






  

 

1
1 1
1 1 i
j
n
ij
k
jij
k
jiji
ii
k
i xaxab
a
x

xk+1=Exk+f iteration for Jacobi method
A can be written as A=L+D+U (not
decomposition)











































000
00
0
00
00
00
0
00
000
23
1312
33
22
11
3231
21
333231
232221
131211
a
aa
a
a
a
aa
a
aaa
aaa
aaa






  



n
ij
k
jij
i
j
k
jiji
ii
k
i xaxab
a
x
1
1
1
1 1 xk+1=-D-1(L+U)xk+D-1b
E=-D-1(L+U)
f=D-1b
Ax=b  (L+D+U)x=b Dxk+1 =-(L+U)xk+b
 
kk
UxLxDxk+1

Gauss-Seidel (GS) iteration
nnnnnn
nn
nn
bxaxaxa
bxaxaxa
bxaxaxa







2211
22222121
11212111















0
0
2
0
1
0
nx
x
x
x







  

 

1
1 1
11 1 i
j
n
ij
k
jij
k
jiji
ii
k
i xaxab
a
x
)(
1 0
1
0
2121
11
1
1 nn xaxab
a
x  
)(
1 1
11
1
22
1
11
1
 nnnnnn
nn
n xaxaxab
a
x 
)(
1 0
2
0
323
1
1212
22
1
2 nn xaxaxab
a
x  
Use the latest
update

Gauss-Seidel Method
An iterative method.
Basic Procedure:
-Algebraically solve each linear equation for xi
-Assume an initial guess solution array
-Solve for each xi and repeat
-Use absolute relative approximate error after each iteration
to check if error is within a pre-specified tolerance.

Gauss-Seidel Method
Algorithm
A set of n equations and n unknowns:
11313212111 ... bxaxaxaxa nn 
2323222121 ... bxaxaxaxa n2n 
nnnnnnn bxaxaxaxa  ...332211
. .
. .
. .
If: the diagonal elements are
non-zero
Rewrite each equation solving
for the corresponding unknown
ex:
First equation, solve for x1
Second equation, solve for x2

Gauss-Seidel Method
Algorithm
Rewriting each equation
11
13132121
1
a
xaxaxac
x nn


nn
nnnnnn
n
nn
nnnnnnnnn
n
nn
a
xaxaxac
x
a
xaxaxaxac
x
a
xaxaxac
x
11,2211
1,1
,122,122,111,11
1
22
23231212
2














From Equation 1
From equation 2
From equation n-1
From equation n

Gauss-Seidel Method
Algorithm
General Form of each equation
11
1
1
11
1
a
xac
x
n
j
j
jj




22
2
1
22
2
a
xac
x
j
n
j
j
j




1,1
1
1
,11
1







nn
n
nj
j
jjnn
n
a
xac
x
nn
n
nj
j
jnjn
n
a
xac
x





1

Derivation of the Trapezoidal Rule

Method Derived From Geometry
The area under the
curve is a trapezoid.
The integral
trapezoidofAreadxxf
b
a
 )(
)height)(sidesparallelofSum(
2
1

  )ab()a(f)b(f 
2
1



 

2
)b(f)a(f
)ab(
Figure 2: Geometric Representation
f(x)
a b

b
a
dx)x(f1
y
x
f1(x)

Multiple Segment Trapezoidal Rule
f(x)
a b
y
x
4
ab
a


4
2
ab
a


4
3
ab
a


Figure 4: Multiple (n=4) Segment Trapezoidal Rule
Divide into equal segments as
shown in Figure 4. Then the
width of each segment is:
n
ab
h


The integral I is:

b
a
dx)x(fI

What is Integration?
Integration

b
a
dx)x(fI
The process of measuring the
area under a curve.
Where:
f(x) is the integrand
a= lower limit of integration
b= upper limit of integration
f(x)
a b
y
x

b
a
dx)x(f

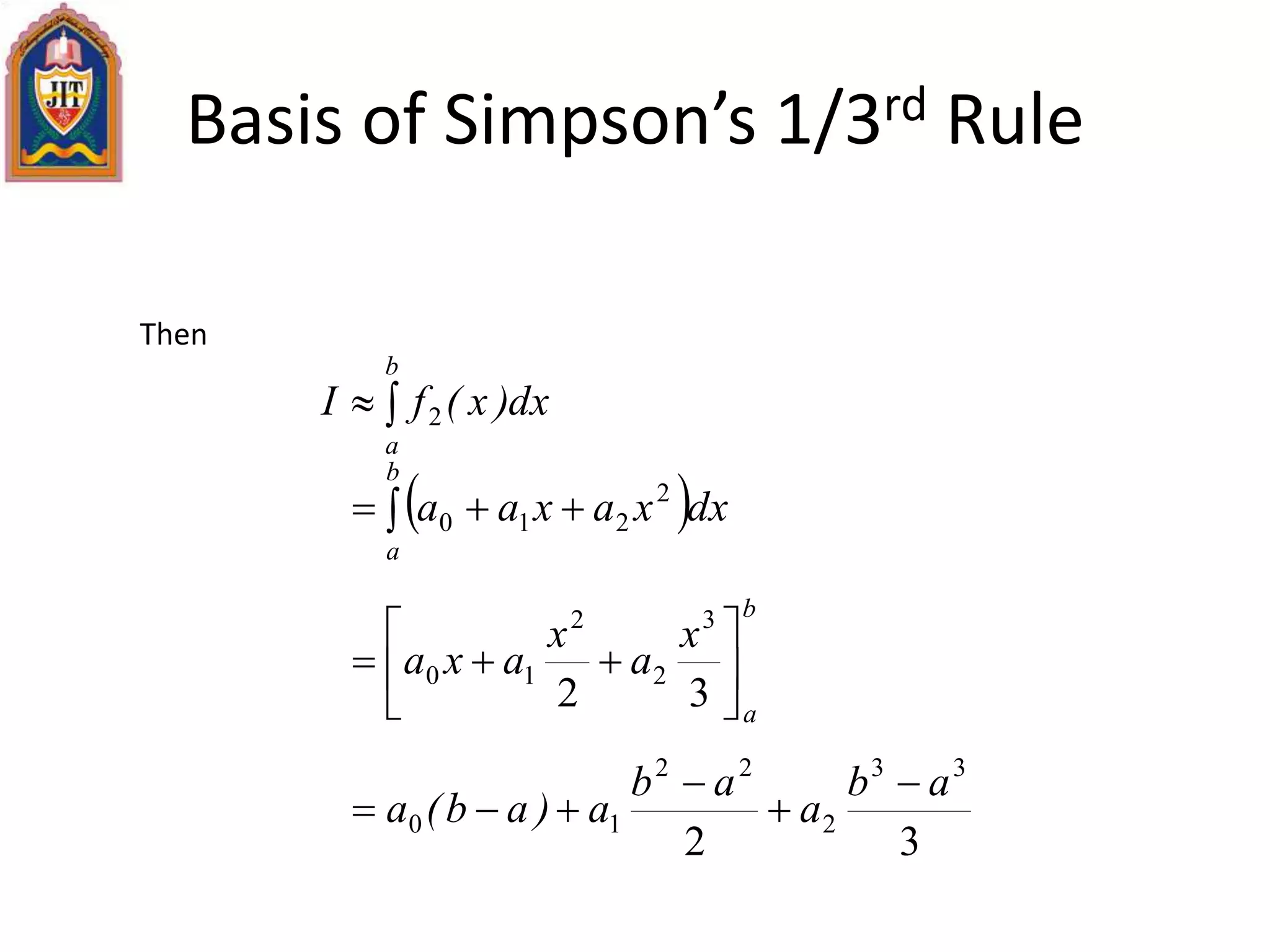
Basis of Simpson’s 1/3rd Rule
Trapezoidal rule was based on approximating the integrand by a first
order polynomial, and then integrating the polynomial in the interval of
integration. Simpson’s 1/3rd rule is an extension of Trapezoidal rule
where the integrand is approximated by a second order polynomial.
Hence
 
b
a
b
a
dx)x(fdx)x(fI 2
Where is a second order polynomial.)x(f2
2
2102 xaxaa)x(f 

Choose
)),a(f,a( ,
ba
f,
ba











 
22
))b(f,b(and
as the three points of the function to evaluate a0, a1 and a2.
2
2102 aaaaa)a(f)a(f 
2
2102
2222





 





 





 





  ba
a
ba
aa
ba
f
ba
f
2
2102 babaa)b(f)b(f 

Solving the previous equations for a0, a1 and a2 give
22
22
0
2
2
4
baba
)a(fb)a(abf
ba
abf)b(abf)b(fa
a






 


221
2
2
433
2
4
baba
)b(bf
ba
bf)a(bf)b(af
ba
af)a(af
a






 





 


222
2
2
22
baba
)b(f
ba
f)a(f
a












 



Then

b
a
dx)x(fI 2
  
b
a
dxxaxaa 2
210
b
a
x
a
x
axa 






32
3
2
2
10
32
33
2
22
10
ab
a
ab
a)ab(a





Substituting values of a0, a1, a 2 give









 


 )b(f
ba
f)a(f
ab
dx)x(f
b
a 2
4
6
2
Since for Simpson’s 1/3rd Rule, the interval [a, b] is broken
into 2 segments, the segment width
2
ab
h












 
 )b(f
ba
f)a(f
h
dx)x(f
b
a 2
4
3
2
Hence
Because the above form has 1/3 in its formula, it is called Simpson’s 1/3rd Rule.

Multiple Segment Simpson’s 1/3rd Rule
Just like in multiple segment Trapezoidal Rule, one can subdivide the interval
[a, b] into n segments and apply Simpson’s 1/3rd Rule repeatedly over
every two segments. Note that n needs to be even. Divide interval
[a, b] into equal segments, hence the segment width
n
ab
h

  
nx
x
b
a
dx)x(fdx)x(f
0
where
ax 0 bxn 

.
.
Apply Simpson’s 1/3rd Rule over each interval,
...
)x(f)x(f)x(f
)xx(dx)x(f
b
a



 

6
4 210
02
...
)x(f)x(f)x(f
)xx( 


 

6
4 432
24
f(x)
. . .
x0 x2 xn-2 xn
x
.....dx)x(fdx)x(fdx)x(f
x
x
x
x
b
a
 
4
2
2
0





n
n
n
n
x
x
x
x
dx)x(fdx)x(f....
2
2
4

...
)x(f)x(f)x(f
)xx(... nnn
nn 


 
 

6
4 234
42



 
 

6
4 12
2
)x(f)x(f)x(f
)xx( nnn
nn
Since
hxx ii 22  
n...,,,i 42

Then
...
)x(f)x(f)x(f
hdx)x(f
b
a



 

6
4
2 210
...
)x(f)x(f)x(f
h 


 

6
4
2 432
...
)x(f)x(f)x(f
h nnn



 
 
6
4
2 234



 
 
6
4
2 12 )x(f)x(f)x(f
h nnn


b
a
dx)x(f   ...)x(f...)x(f)x(f)x(f
h
n  1310 4
3
  )}]()(...)()(2... 242 nn xfxfxfxf  








 






)()(2)(4)(
3
2
2
1
1
0 n
n
eveni
i
i
n
oddi
i
i xfxfxfxf
h










 






)()(2)(4)(
3
2
2
1
1
0 n
n
eveni
i
i
n
oddi
i
i xfxfxfxf
n
ab

Simpson 3/8 Rule for Integration
The main objective of this chapter is to develop
appropriate formulas for approximating the
integral of the form

Euler’s Method
We have previously seen Euler’s Method for estimating the solution of a differential
equation. That is to say given the derivative as a function of x and y (i.e. f(x,y)) and an
initial value y(x0)=y0 and a terminal value xn we can generate an estimate for the
corresponding yn. They are related in the following way:









xyxfyy
xxx
yx
kkkk
kk
kk
),(
),(
1
1
11
The value x = (xn-x0)/n and the accuracy increases with n.
Taylor Method of Order 1
Euler’s Method is one of a family of methods for solving differential equations
developed by Taylor. We would call this a Taylor Method of order 1. The 1 refers to the
fact that this method used the first derivative to generate the next estimate. In terms
of geometry it says you are moving along a line (i.e. the tangent line) to get from one
estimate to the next.

Find the second derivative if the first derivative is given to the
right.
Set f(x,y) = x2y and plug it into the formula below.
yx
dx
dy 2

dx
dy
y
f
x
f
dx
yd






2
2
  yxxxy 22
2 
Here we notice that:
2
2 x
y
f
andxy
x
f






yxxy 4
2 
Higher Derivatives
Third, fourth, fifth, … etc derivatives can be
computed with the same method. This has
a recursive definition given to the right.



















dx
dy
dx
yd
ydx
yd
xdx
yd
n
n
n
n
n
n
1
1

Picard Iteration
The Picard method is a way of approximating solutions of ordinary differential
equations. Originally it was a way of proving the existence of solutions. It is only
through the use of advanced symbolic computing that it has become a practical
way of approximating solutions.
In this chapter we outline some of the numerical methods used to approximate
solutions of ordinary differential equations. Here is a reminder of the form of a
differential equation.
The first step is to transform the differential equation and its initial condition
into an integral

Runge-Kutta 4th Order Method
where
 hkkkkyy ii 43211 22
6
1

 ii yxfk ,1 






 hkyhxfk ii 12
2
1
,
2
1






 hkyhxfk ii 23
2
1
,
2
1
 hkyhxfk ii 34 , 
For
0)0(),,( yyyxf
dx
dy

Runge Kutta 4th order method is given by

How to write Ordinary Differential
Equation
  50,3.12  
yey
dx
dy x
is rewritten as
  50,23.1  
yye
dx
dy x
In this case
  yeyxf x
23.1,  
How does one write a first order differential equation in the form of
 yxf
dx
dy
,

Fourier Cosine & Sine Integrals
IntegralSineFourier:)sin()()(,0)(
)sin()(
1
oddisf(x)functiontheIf
IntegralCosineFourier:)cos()()(
0)(
)cos()(
2
)(
1
)(
1
)cos()(
1
A(w)evenisf(x)functiontheIf
0
0
00
0



















dwwxwBxfwA
dvwvvfB(w)
dwwxwAxf
wB
dvwvvfdvdv
dvwvvf




Example
dwwx
w
w
dwwxwAf(x)
dvwvdvwvvfwB
w
w
dvwvdvwvvfwA
f(x)
)cos(
)sin(2
)cos()(
isfofintegralFourierThe
0)sin(
1
)sin()(
1
)(
)sin(2
)cos(
1
)cos()(
1
)(
1xfor0
1x1-for1
Let
00
1
1
1
1
1
1





















2 1 0 1 2
0
1
1.5
0.5
f 10 x( )
f 100 x( )
g x( )
22 x
f10 integrate from 0 to 10
f100 integrate from 0 to 100
g(x) the real function

Similar to Fourier series approximation, the Fourier integral approximation
improves as the integration limit increases. It is expected that the integral will
converges to the real function when the integration limit is increased to infinity.
Physical interpretation: The higher the integration limit means more higher
frequency sinusoidal components have been included in the approximation.
(similar effect has been observed when larger n is used in Fourier series
approximation) This suggests that w can be interpreted as the frequency of each
of the sinusoidal wave used to approximate the real function.
Suggestion: A(w) can be interpreted as the amplitude function of the specific
sinusoidal wave. (similar to the Fourier coefficient in Fourier series expansion)

Fourier Cosine Transform
)(ˆoftransformcosineFourierinversetheis)(
)cos()(ˆ2
)cos()()(
f(x)oftransformcosineFourierthecalledis)(ˆ
by xreplacedbeenhas,)cos()(
2
)(
2
)(ˆ
)(ˆ2
Define
.)cos()(
2
)(where,)cos()()(
:f(x)functionevenanFor
00
0
00
wfxf
dwwxwfdwwxwAxf
wf
vdxwxxfwAwf
wfA(w)
dvwvvfwAdwwxwAxf
c
c
c
c
c
















Fourier Sine Transform
)(ˆoftransformsineFourierinversetheis)(
)sin()(ˆ2
)sin()()(
f(x)oftransformsineFourierthecalledis)(ˆ
by xreplacedbeenhas,)sin()(
2
)(
2
)(ˆ
)(ˆ2
Define
.)sin()(
2
)(where,)sin()()(
:f(x)functionoddanforSimilarly,
00
0
00
wfxf
dwwxwfdwwxwBxf
wf
vdxwxxfwBwf
wfB(w)
dvwvvfwBdwwxwBxf
S
S
S
S
S
















Improper Integral of Type 1
a) If exists for every number t ≥ a, then
provided this limit exists (as a finite number).
b) If exists for every number t ≤ b, then
provided this limit exists (as a finite number).
The improper integrals and are called
convergent if the corresponding limit exists and divergent
if the limit does not exist.
c) If both and are convergent, then we
define

t
a
dxxf )(

b
t
dxxf )(




t
aa
t
dxxfdxxf )()( lim



b
t
b
t
dxxfdxxf )()( lim


a
dxxf )( 
a
dxxf )(


a
dxxf )(  
b
dxxf )(






a
a
dxxfdxxfdxxf )()()(

Examples
1
1
11111
.1 limlimlim 1
1 21 2











 tx
dx
x
dx
x t
t
t
t
t
    1.2 0000
limlimlim 

 
t
t
t
x
t
t
x
t
x
eeedxedxe
   
    
























  
22
tantan
tantan
1
1
1
1
1
1
.3
11
0
101
0
0 222
limlim
limlim
tt
xx
dx
x
dx
x
dx
x
tt
t
t
t
t
All three integrals are convergent.

    


 1lnlnln
11
limlimlim 111
txdx
x
dx
x t
t
t
t
t
An example of a divergent integral:
The general rule is the following:
1pifdivergentand1pifconvergentis
1
1


dx
xp


1 2
convergentis
1
thatslidepreviousthefromRecall dx
x

Definition of an Improper Integral of Type 2
a) If f is continuous on [a, b) and is discontinuous at b, then
if this limit exists (as a finite number).
a) If f is continuous on (a, b] and is discontinuous at a, then
if this limit exists (as a finite number).
The improper integral is called convergent if the
corresponding limit exists and divergent if the limit does
not exist.
c) If f has a discontinuity at c, where a < c < b, and both
and are convergent, then we define
 


t
a
b
a
bt
dxxfdxxf )()( lim
 


b
t
b
a
at
dxxfdxxf )()( lim

b
c
dxxf )(
c
a
dxxf )(

b
a
dxxf )(
 
b
c
c
a
b
a
dxxfdxxfdxxf )()()(

Engg. mathematics iii

More Related Content

What's hot

Similar to Engg. mathematics iii

Recently uploaded

Engg. mathematics iii