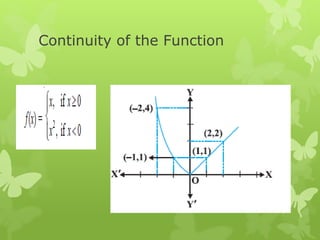
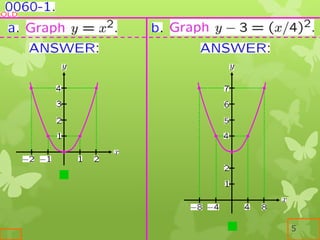
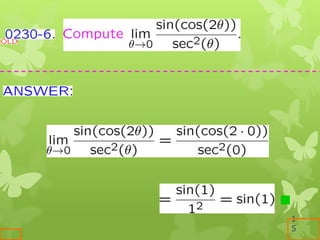
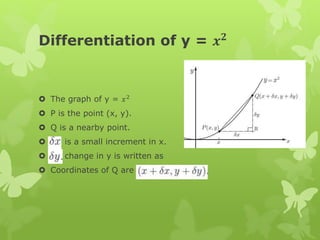
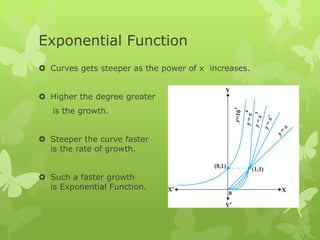
The document discusses key concepts in calculus including continuity, differentiation, integration, and their applications. It defines continuity as being able to draw a function's graph without lifting the pen, and differentiation as computing the rate of change of a dependent variable with respect to changes in the independent variable. The document also covers differentiation rules and techniques for implicit, inverse, exponential, logarithmic, and parametric functions.