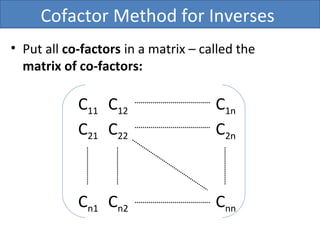
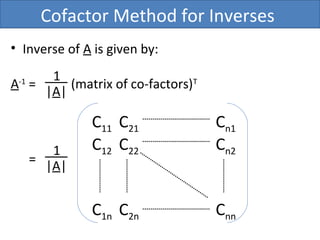
The document describes the cofactor method for finding the inverse of a matrix A. It defines the cofactor Cij as the signed determinant of the matrix made by removing row i and column j from A. The inverse is then given by the transpose of the matrix of cofactors divided by the determinant of A. An example calculates the inverse of the 2x2 matrix A = [a, c; b, d] using this method.

1. Cofactor Method for Inverses
• Let A = (aij) be an nxn matrix
• Recall, the co-factor Cij of element aij is:
Cij = (-1)i+j
|Mij|
• Mij is the (n-1) x (n-1) matrix made by
removing the ROW i and COLUMN j of A

2. Cofactor Method for Inverses
• Put all co-factors in a matrix – called the
matrix of co-factors:
C11 C12 C1n
C21
Cn1
C22
Cn2
C2n
Cnn

3. Cofactor Method for Inverses
• Inverse of A is given by:
A-1
= (matrix of co-factors)T1
|A|
1
|A|
C11 C21 Cn1
C12
C1n
C22
C2n
Cn2
Cnn
=

4. Examples
• Calculate the inverse of A =
a
c
b
d
|M11| = d C11 = dM11 = d

5. Examples
• Calculate the inverse of A =
a
c
b
d
|M12| = c C12 = -cM12 = c

6. Examples
• Calculate the inverse of A =
a
c
b
d
|M21| = b C12 = -bM21 = b

7. Examples
• Calculate the inverse of A =
a
c
b
d
|M22| = a C22 = aM22 = a

8. Examples
• Calculate the inverse of A =
a
c
b
d
• Found that:
C22 = aC21 = -bC12 = -cC11 = d
• So,
A-1
= (matrix of co-factors)T1
|A|

9. Examples
• Calculate the inverse of A =
a
c
b
d
• Found that:
C22 = aC21 = -bC12 = -cC11 = d
• So,
A-1
= (matrix of co-factors)T1
(ad-bc)

10. Examples
• Calculate the inverse of A =
a
c
b
d
• Found that:
C22 = aC21 = -bC12 = -cC11 = d
• So,
A-1
= 1
(ad-bc)
C11
C21
C12
C22
T

11. Examples
• Calculate the inverse of A =
a
c
b
d
• Found that:
C22 = aC21 = -bC12 = -cC11 = d
• So,
A-1
= 1
(ad-bc)
C11
C12
C21
C22

12. Examples
• Calculate the inverse of A =
a
c
b
d
• Found that:
C22 = aC21 = -bC12 = -cC11 = d
• So,
A-1
= 1
(ad-bc)
d
C12
C21
C22

13. Examples
• Calculate the inverse of A =
a
c
b
d
• Found that:
C22 = aC21 = -bC12 = -cC11 = d
• So,
A-1
= 1
(ad-bc)
d
C12
-b
C22

14. Examples
• Calculate the inverse of A =
a
c
b
d
• Found that:
C22 = aC21 = -bC12 = -cC11 = d
• So,
A-1
= 1
(ad-bc)
d
-c
-b
C22

15. Examples
• Calculate the inverse of A =
a
c
b
d
• Found that:
C22 = aC21 = -bC12 = -cC11 = d
• So,
A-1
= 1
(ad-bc)
d
-c
-b
a

16. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Find the co-factors:
2
2
1
43
C11 = 2|M11| = 2M11 = 2 2
43

17. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Find the co-factors:
2
2
1
43
C12 = 0|M12| = 0M12 = 1 2
42

18. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Find the co-factors:
2
2
1
43
C13 = -1|M13| = -1M13 = 1 2
32

19. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Find the co-factors:
2
2
1
43
C21 = -1|M21| = 1M21 = 1 1
43

20. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Find the co-factors:
2
2
1
43
C22 = 2|M22| = 2M22 = 1 1
42

21. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Find the co-factors:
2
2
1
43
C23 = -1|M23| = 1M23 = 1 1
32

22. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Find the co-factors:
2
2
1
43
C31 = 0|M31| = 0M31 = 1 1
22

23. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Find the co-factors:
2
2
1
43
C32 = -1|M32| = 1M32 = 1 1
21

24. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• First find the co-factors:
2
2
1
43
C33 = 1|M33| = 1M33 = 1 1
21

25. Examples 3x3 Matrix
• Calculate the inverse of B =
1
1
1
2
• Next the determinant: use the top row:
2
2
1
43
|B| = 1x |M11| -1x |M12| + 1x |M13|
= 2 – 0 + (-1) = 1

26. • Using the formula,
B-1
= (matrix of co-factors)T1
|B|
= (matrix of co-factors)T1
1
Examples 3x3 Matrix

27. Examples 3x3 Matrix
2
-1
0
2 -1
0
1
1-1
• Using the formula,
B-1
= (matrix of co-factors)T1
|B|
=
1
1
T

28. 2
0
-1
2 -1
-1
0
1-1
Examples 3x3 Matrix
• Using the formula,
B-1
= (matrix of co-factors)T1
|B|
=
• Same answer obtained by Gauss-Jordan method