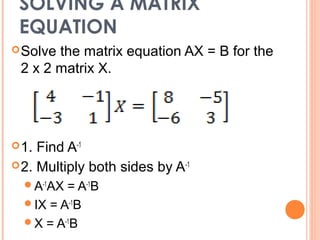
The document discusses identity matrices, inverses of matrices, and methods for finding inverses. It defines an identity matrix as a diagonal matrix with 1s and 0s. It states that two matrices A and B are inverses if AB = BA = I. The inverse of a 2x2 matrix A can be found by taking the adjugate of A and dividing by the determinant. To solve a matrix equation AX=B, we multiply both sides by the inverse of A. Not all matrices have inverses, as a matrix only has an inverse if its determinant is not equal to 0.

1. 4.4 IDENTITY AND
INVERSE MATRICES

2. THE IDENTITY MATRIX
 For n x n matrices, the identity matrix
has 1’s on the diagonal and 0’s
everywhere else.
 2 x 2 Identity Matrix:
3 x 3 Identity Matrix:
 If A is n x n, then IA = A and AI = A

3. INVERSES
Two n x n matrices, A and B, are
inverses if:
AB = I and BA = I
Inverse of A is written: A-1
So, AA-1 = I = A-1A

4. FINDING THE INVERSE (2 X
2)
 For A=
 Example: Find the inverse of A =

5. SOLVING A MATRIX
EQUATION
 Solvethe matrix equation AX = B for the
2 x 2 matrix X.
 1. Find A-1
 2. Multiply both sides by A-1
A-1AX = A-1B
IX = A-1B
X = A-1B

6. NO INVERSE?
 Not all matrices have an inverse!
 If det A = 0 : A has No Inverse

7. INVERSE OF A 3 X 3
 Use the graphing calculator!
 Find the inverse of A.