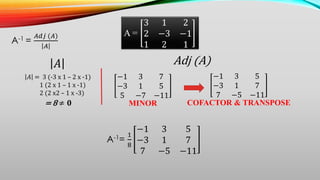
The document provides a comprehensive overview of various types of matrices, including row, column, square, diagonal, scalar, identity, equal, negative, upper and lower triangular, symmetric, and skew symmetric matrices, along with their definitions and examples. Additionally, it covers matrix operations such as addition, subtraction, multiplication, determinants, minors, cofactors, and adjoints, as well as the method of matrix inversion for solving linear equations. Key mathematical concepts and calculations related to matrices are illustrated through numerous examples.

1. ISHANT JAIN, MALHAR SHAH,MEET DOSHI

2. 2 3 −5
1 2 4
6 5 0
MEANING: -
m x n real numbers arranged in m rows and n columns and enclosed by a pair of
brackets is called m x n matrix.

3. TYPES
OF
MATRIX
Row Matrix
Column Matrix
Null Matrix/ Zero Matrix
Square Matrix
Diagonal Matrix
Scalar Matrix
Identity Matrix or Unit Matrix
Equal Matrix
Negative Matrix
Upper Triangular Matrix
Lower Triangular Matrix
Symmetric Matrix
Skew Symmetric Matrix

4. Sr.
No.
Type of Matrix Meaning Example
1. Row Matrix  A matrix consisting of a single row.
 Also called as row vector.
1 2 3
2. Column Matrix  A matrix consisting of a single column.
 Also called as column vector.
1
2
3
3. Null Matrix  All the elements are zero.
 Also known as zero matrix.
 Denoted by “O”.
0 0
0 0
4. Square Matrix  Matrix having same number of rows and columns.
 It can also be written as An.
2 3
4 5
2 1 3
1 6 2
5 2 4
5. Diagonal Matrix  All elements are zero except main or principal diagonal. 2 0
0 5
3 0 0
0 4 0
0 0 1
6. Scalar Matrix  All the diagonal elements are same. 3 0
0 3
2 0 0
0 2 0
0 0 2
7. Unit Matrix  A scalar matrix in which each diagonal element is 1.
 Also called “Identity matrix”.
 Denoted by In.
 Every unit matrix is a diagonal matrix and also a scalar matrix.
1 0
0 1
1 0 0
0 1 0
0 0 1

5. Sr.
No.
Type of Matrix Meaning Example
8. Equal Matrix  Two matrices having the same order.
 Each element of A= Corresponding to the element of B
A=
2 3
1 0
B=
4
2 9
2 − 1 0
9. Negative Matrix  Replacing all the elements with its additive inverse.
A=
3 −1
−2 4
5 −3
B=
−3 1
2 −4
−5 3
10. Upper Triangular
Matrix
 A square matrix in which all elements below the principal
diagonal are zero.
1 3 7
0 2 8
0 0 7
11. Lower Triangular
Matrix
 A square matrix in which all elements above the principal
diagonal are zero.
1 0 0
3 6 0
2 5 7
12. Symmetric Matrix
 A square matrix having aij=aji
2 1 3
1 6 2
3 2 4
13. Skew Symmetric Matrix
 A square matrix having aij= -aji
2 1 3
−1 6 2
−3 −2 4
a12 =a21
a13 =a31
a23 =a32
a12 =-a21
a13 =-a31
a23 =-a32

6. 1. Matrix Addition
2. Matrix Subtraction
3. Scalar Multiplication
4. Matrix Multiplication

7. 4 6
0 2
3 2
8 5
7 8
8 7

8. 9 7
5 8
5 3
0 2
4 4
5 6

9. 4 3
6 9
12 09
18 27

10. 2 5
7 1
7 5
-3 0
-1 10
46 35

12.  Determinant is a scalar value that is calculated from a matrix.
 It can only be calculated for a square matrix.
 It is denoted by ∆ (Delta).
 Calculation For 2X2 Matrix
1 3
5 6
(1 x 6) –
(3 x 5) - 9

13. 03 05 02
04 00 01
−2 06 10
3{(0 X 10) – (1 X 6)} –
5{(4 X 10) – (-2 X 1)} +
2{(4 X 6) – (-2 X 0)}
- 180

14. MEANING: -
The minor of a element in a matrix is the determinant obtained by deleting the row
and the column in which that element appears.
 Minor of a particular element in a matrix
8 2 4
6 0 7
3 5 9
Step 1:-Ignore the row and column in which the
element a11 i.e. 8 is
Step 2: -Write the remaining elements in determinant
form
0 7
5 9
0 7
5 9
Minor of particular element is
(-35)

15. 8 2 4
6 0 7
3 5 9
0 7
5 9
6 7
3 9
6 0
3 5
2 4
5 9
8 4
3 9
8 2
3 5
2 4
0 7
8 4
6 7
8 2
6 0
 Minor of a Matrix
−35 33 30
−2 60 34
14 32 −12
Minor
Matrix

16. In some cases, minor and
co-factor remains same but
it may be different or there
may be difference of minus.
Cij = (-1)i+j Mij
Cij = co-factor of aij
Mij = minor of aij
a11 a12 a13
b21 b22 b23
c31 c32 c33
C11= (-1)1+1 M11
C11 =(-1)2 M11
C11= M11
a11 a12 a13
b21 b22 b23
c31 c32 c33
C12= (-1)1+2M12
C12 =(-1)3 M12
C12= -M12

17. MEANING: -
The Adjoint of A is the transposed matrix of cofactors of A.
Adjoint of a Square Matrix of order 2 x 2
Step 1:- Change the position of principal element i.e.
2 & 3.
Step 2:- Change the sign of remaining two elements
i.e. -1 & -5.
2 5
1 3
3
2
3 −5
−1 2

18.  Adjoint of a Square Matrix of order
3 x 3
−1 2 4
1 0 2
3 1 −1
Step 1:- Find out the minor matrix of given
matrix. 0 2
1 −1
1 2
3 −1
1 0
3 1
2 4
1 −1
−1 4
3 −1
−1 2
3 1
2 4
0 2
−1 4
1 2
−1 2
1 0
Step 2:- Find out the Cofactor matrix of
Obtained matrix i.e.
+ − +
− + −
+ − +
−2 −7 1
−6 −11 −7
4 −6 −2
−2 7 1
6 −11 7
4 6 −2
Step 3:- Find out the Transpose of Obtained
matrix.
−𝟐 𝟔 𝟒
𝟕 −𝟏𝟏 𝟔
𝟏 𝟕 −𝟐

19. 







1
3
5
7
4
2
3
2 A
A
2x3












1
7
3
4
5
2
3
2
T
T
A
A
T
ji
ij a
a  For all i and j
Interchange rows and columns
Then transpose of A, denoted AT
.
The dimensions of AT are the reverse
of the dimensions of A

20. MEANING: -
Consider a scalar k. The inverse is the reciprocal or division of 1 by the scalar.
Example: k=7 the inverse of k or k-1 = 1/k = 1/7

21. A-1 =
𝐴𝑑𝑗 (𝐴)
𝐴
A =
3 1 2
2 −3 −1
1 2 1
= 8 ≠ 𝟎
𝐴 = 3 (-3 x 1 – 2 x -1)
1 (2 x 1 – 1 x -1)
2 (2 x2 – 1 x -3)
𝐴
−1 3 7
−3 1 5
5 −7 −11
MINOR
Adj (A)
−1 3 5
−3 1 7
7 −5 −11
COFACTOR & TRANSPOSE
A-1=
1
8
−1 3 5
−3 1 7
7 −5 −11

23. MEANING: -
It is Solution by the method of inversion of the coefficient matrix.
3x + y + 2z = 3
2x +3y – z = -3
x + 2y + z = 4
Step 1:- Let A = Coefficient Matrix. A =
3 1 2
2 −3 −1
1 2 1
Step 2:- Let X= Unknown Matrix. X =
𝑥
𝑦
𝑧
Step 3:- Let B= Constant Matrix. B =
3
−3
4
X = A-1B Required Solution

24. A-1 =
𝐴𝑑𝑗 (𝐴)
𝐴
−1 3 7
−3 1 5
5 −7 −11
MINOR
A =
3 1 2
2 −3 −1
1 2 1
= 8 ≠ 𝟎
Adj (A)
𝐴 = 3 (-3 x 1 – 2 x -1)
1 (2 x 1 – 1 x -1)
2 (2 x2 – 1 x -3)
𝐴
−1 3 5
−3 1 7
7 −5 −11
COFACTOR & TRANSPOSE
A =
3 1 2
2 −3 −1
1 2 1
A-1=
1
8
−1 3 5
−3 1 7
7 −5 −11
𝑥
𝑦
𝑧
=
1
8
−1 3 5
−3 1 7
7 −5 −11
X
3
−3
4
As, X = A-1B
𝑥
𝑦
𝑧
=
1
2
−1
X = 1
Y = 2 Ans.
Z = -1

25. x - 3y = 5
2x + y = 4
=
∆
∆
x
1
=
∆
∆
y
2
SOLUTIONS ARE: -
∆ =
01 −3
02 01
= 7
∆1 =
05 −3
04 01
= 17
∆2 =
01 05
02 04
= -6
x=
17
7
y=
−6
7

26. x+2y+3z =1
x+3y+5z =2
2x+5y+9z =3
Step 1:- Let A = Coefficient Matrix. A =
1 2 3
1 3 5
2 5 9
Step 2:- Let X= Unknown Matrix. X =
𝑥
𝑦
𝑧
Step 3:- Let B= Constant Matrix. B =
1
2
3
Step 4:- Convert coefficient matrix into upper triangular matrix.

27. A =
1 2 3
1 3 5
2 5 9
𝑥
𝑦
𝑧
=
1
2
3
~
1 2 3
0 1 2
0 1 3
X=
1
1
1
R2 – R1
R3 - 2R1
R3 – R2 ~
1 2 3
0 1 2
0 0 1
X =
1
1
0
Step 5:- Convert matrix form into equation again.
1x+2y+3z=1 …….(1)
0x+1y+2z=1 …….(2)
0x+0y+1z=0 …….(3)
From 3rd Eqn
From 2nd Eqn
y+2z=1
y=1
z=0
x+2y+3z=1
x+2+0=1
x= -1
From 1st Eqn
X = -1
Y = 1 Ans.
Z = 0

28. 1.
• If |A|≠ 0 𝑛𝑜𝑛 − 𝑠𝑖𝑛𝑔𝑢𝑙𝑎𝑟 𝑚𝑎𝑡𝑟𝑖𝑥 𝑡ℎ𝑒𝑛 𝐴−1
𝑒𝑥𝑖𝑠𝑡𝑠
2.
• Let A = In∙ 𝐴 ; 𝑤ℎ𝑒𝑟𝑒 In= 𝑖𝑑𝑒𝑛𝑡𝑖𝑡𝑦 𝑚𝑎𝑡𝑟𝑖𝑥 𝑜𝑓 𝑜𝑟𝑑𝑒𝑟 ′𝑛′
3.
• Convert A=In∙A into In=BA
4.
• Convert B=𝐴−1

29. A =
1 0 −1
2 −1 3
1 −1 0
|A|=1
−1 3
−1 0
-0
2 3
1 0
+(-1)
2 −1
1 −1
= 1(3)-0(3)+(-1)(-1)
 |A| = 4 ≠ 0
𝐴
1 0 −1
2 −1 3
1 −1 0
=
1 0 0
0 1 0
0 0 1
A
A=In∙A
~
1 0 −1
0 −1 5
0 −1 1
=
1 0 0
−2 1 0
−1 0 1
A
𝑅2 − 2𝑅1
𝑅3 − 𝑅1
~
1 0 −1
0 −1 5
0 0 −4
=
1 0 0
−2 1 0
1 −1 1
A 𝑅3 − 𝑅2

30. 1 0 −1
0 −1 5
0 0 1
=
1 0 0
−2 1 0
−1
4
1
4
−1
4
A −𝑅3
4
1 0 −1
0 1 −5
0 0 1
=
1 0 0
2 −1 0
−1
4
1
4
−1
4
A −R2
𝐴−1 =
3
4
1
4
−1
4
3
4
1
4
−5
4
−1
4
1
4
−1
4
1 0 0
0 1 0
0 0 1
=
3
4
1
4
−1
4
3
4
1
4
−5
4
−1
4
1
4
−1
4
A
R1 + R3
R2 + 5R3 In=BA
B=𝐴−1