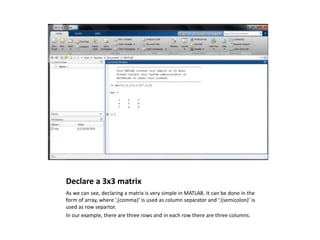
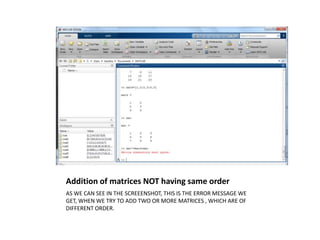
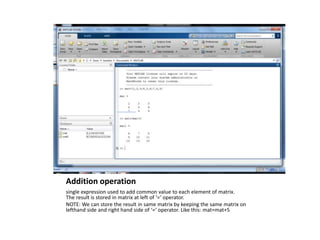
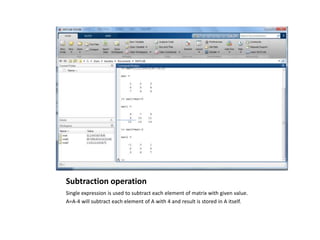
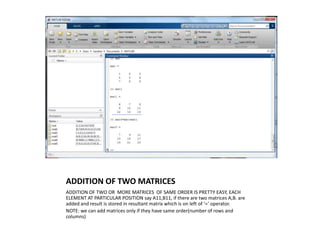
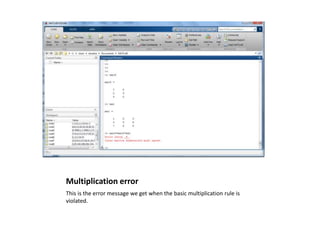
This document provides an overview of basic mathematical operations in MATLAB for beginners, including: 1) Defining matrices using commas and semicolons to separate columns and rows. 2) Single expression operations can add, subtract, multiply or divide each element of a matrix by a scalar value. 3) Matrices can only be added or subtracted if they have the same order (number of rows and columns), and matrices can only be multiplied if the number of columns in the first equals the number of rows of the second.

1. MATLAB Learning for Beginners
This is my first presentation on basic
mathematical operations in MATLAB.

2. Declare a 3x3 matrix
As we can see, declaring a matrix is very simple in MATLAB. It can be done in the
form of array, where ‘,(comma)’ is used as column separator and ‘;(semicolon)’ is
used as row separtor.
In our example, there are three rows and in each row there are three columns.

3. Addition operation
single expression used to add common value to each element of matrix.
The result is stored in matrix at left of ‘=‘ operator.
NOTE: We can store the result in same matrix by keeping the same matrix on
lefthand side and right hand side of ‘=‘ operator. Like this: mat=mat+5

4. Subtraction operation
Single expression is used to subtract each element of matrix with given value.
A=A-4 will subtract each element of A with 4 and result is stored in A itself.

5. Multiplication operation
To multiply each element of matrix we use multiplication expression.
A=A*4 ie every element of A is multiplied by 4 and stored back into
matrix A.

6. DIVISION OPERATION
Like other mathematical operations, division is also a single expression task,
the result is upto four digits of decimal.
A=A/3 , the result of this expression will be each element of A is replaced by
quotient after division by 3

7. Power operation
A=A.^n here n is the value of power, this expression will result as ‘each
element of matrix A is raised to power n . As in our example we have raised
every element of matrix mat to 2 and save the resultant matrix as mat11

8. ADDITION OF TWO MATRICES
ADDITION OF TWO OR MORE MATRICES OF SAME ORDER IS PRETTY EASY, EACH
ELEMENT AT PARTICULAR POSITION say A11,B11, if there are two matrices A,B. are
added and result is stored in resultant matrix which is on left of ‘=‘ operator.
NOTE: we can add matrices only if they have same order(number of rows and
columns)

9. Addition of matrices NOT having same order
AS WE CAN SEE IN THE SCREEENSHOT, THIS IS THE ERROR MESSAGE WE
GET, WHEN WE TRY TO ADD TWO OR MORE MATRICES , WHICH ARE OF
DIFFERENT ORDER.

10. Subtraction of two or more matrices
NOTE: DIMENSIONS OF THE MATRICES UNDER OPERATION MUST BE
SAME.

11. Multiplication of two or more matrices
Note: For multiplication operation to be successful, the number of columns of
first matrix must be equal to the number of row s of second matrix.
Ie: if A is a matrix of order mxn and B is a matrix of order nxp, then the
expression C=A*B will result a matrix C of order mxp.

12. Multiplication of two or more matrices
MAT has order 3x3 and mat6 has order 3x2 , thus mat9 = mat*mat6 gives
a new matrix mat9 having order 3x2.

13. Multiplication error
This is the error message we get when the basic multiplication rule is
violated.

14. THANKYOU.