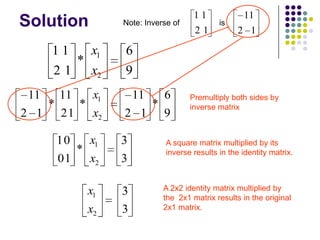
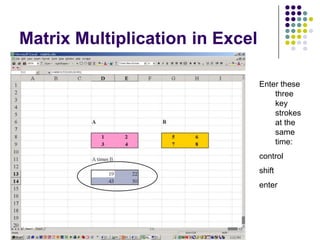
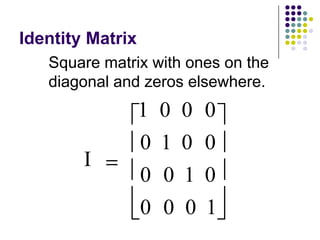
A matrix is a rectangular array of numbers arranged in rows and columns. The order of a matrix describes its dimensions as the number of rows and columns. Matrices can be added or multiplied if they are the same order. Matrix multiplication results in a matrix whose order is the number of rows of the first matrix and columns of the second. The inverse of a square matrix A exists when AA-1=I=A-1A, where I is the identity matrix. The inverse is used to solve systems of linear equations of the form Ax=b by computing x=(A-1)b. Excel can perform matrix operations like multiplication and inversion using formulas.

1. An introduction to
Matrix Algebra

2. Algebra

3. MATRIX
A matrix is an ordered rectangular array of
numbers, arranged in rows and columns.
rows
columns

4. ORDER OF A MATRIX
The size or order of a matrix is
described by its number of rows
and the number of columns.
If a matrix, A, has m rows and n columns
then A is described as an mxn matrix.

5. The numbers in a matrix are called its
elements. The element in the ith row and jth
column of a matrix is generally denoted by
aij. A matrix with m rows and n columns is
written or .

6. Row Matrix
A matrix with just one row is
called a row matrix (or row
vector).
A a1 a 2 , an aj (1 x n)

7. Column Matrix
A matrix with just one column is
called a column matrix.
a1
a2
A ai (m x 1)
am

8. Matrices of the same order
Two matrices which have the Same
number of rows and columns are
said to be matrices of the same
order.

9. Equal Matrices
Two matrices A = (aij) and B = (bij) are said to be equal if,
and only if, each element aij of A is equal to the
corresponding element bij of B.
In symbolic form this reads:
A=B  aij = bij for all i and j
From this it follows that equal matrices are of the same
order but matrices of the same order are not necessarily
equal.

11. Null matrix
Any matrix, all of whose elements are zero, is called
a null or zero matrix and is denoted by O.

12. Matrix Addition
A new matrix C may be defined as the
additive combination of matrices A and
B where: C = A + B
is defined by:
cij aij bij
Note: all three matrices are of the same dimension

13. Addition
a11 a12
If A
a 21 a 22
b11 b12
and B
b 21 b 22
a11 b11 a12 b12
then C
a 21 b 21 a 22 b22

14. Matrix Addition Example
3 4 1 2 4 6
A B C
5 6 3 4 8 10

15. Multiplication by a scalar
 If A is a given matrix and a scalar then
A is the matrix each of whose elements is
times the corresponding element of A.
Thus A

16. The
Identity

17. Identity Matrix
Square matrix with ones on the
diagonal and zeros elsewhere.
1 0 0 0
0 1 0 0
I
0 0 1 0
0 0 0 1

18. Equal Matrices
Two matrices A and B are said
to be equal if, and only if, each
element aij of A is equal to the
corresponding element bij of
B.

19. The Null matrix
Any matrix all of whose elements are zero
is called a null or zero matrix

20. Transpose Matrix
Rows become columns and
columns become rows
a11 a 21 , , am1
a12 a 22 , , am 2
A'
a1n a 2n , , amn

21. Square Matrix
Same number of rows and
columns
5 4 7
B 3 6 1
2 1 3

22. Matrix Subtraction
C = A - B
Is defined by
Cij Aij Bij

23. Matrix Multiplication
 Let A and B be two matrices. If the number of
columns in A is equal to the number of rows
in B we say that A and B are conformable for
the matrix product AB.
 If A is order m n and B is of order n p, then
the product AB is defined and is a matrix of
order m p.

24. Matrix Multiplication
Matrices A and B have these dimensions:
[r x c] and [s x d]

25. Matrix Multiplication
Matrices A and B can be multiplied if:
[m x n] and [n x p]
n=n

26. Matrix Multiplication
The resulting matrix will have the dimensions:
[m x n] and [n x p]
mxp

27. Computation: A x B = C
a11 a12
A
a 21 a 22 [2 x 2]
b11 b12 b13
B
b 21 b 22 b 23
[2 x 3]
a11b11 a12b21 a11b12 a12b22 a11b13 a12b23
C
a 21b11 a 22b21 a 21b12 a 22b22 a 21b13 a 22b23
[2 x 3]

28. Computation: A x B = C
2 3
111
A 11 and B
1 0 2
1 0
[3 x 2] [2 x 3]
A and B can be multiplied
2 *1 3 *1 5 2 *1 3 * 0 2 2 *1 3 * 2 8 528
C 1*1 1*1 2 1*1 1* 0 1 1*1 1* 2 3 213
1*1 0 *1 1 1*1 0 * 0 1 1*1 0 * 2 1 111
[3 x 3]

29. Computation: A x B = C
2 3
111
A 11 and B
1 0 2
1 0
[3 x 2] [2 x 3]
Result is 3 x 3
2 *1 3 *1 5 2 *1 3 * 0 2 2 *1 3 * 2 8 528
C 1*1 1*1 2 1*1 1* 0 1 1*1 1* 2 3 213
1*1 0 *1 1 1*1 0 * 0 1 1*1 0 * 2 1 111
[3 x 3]

30. Note:
 If A is an m n and B is n p matrix, then AB is
an m p matrix. Hence we see that BA is
defined only when p=m.

31. Inversion

32. The Inverse of a Matrix
Definition:
Let A be a square matrix. A matrix B
such that AB=I=BA is called the inverse
matrix of A and is denoted by A-1.
So if A-1 exists, we have AA-1=I=A-1A
and the matrix is said to be invertible.
If a matrix has no inverse, then it is said
to be non-invertible.

33. The Inverse of a Matrix
1 1
A A AA I
Like a reciprocal Like the number one
in scalar math in scalar math

34. Linear System of Simultaneous
Equations
First precinct: 6 arrests last week equally divided
between felonies and misdemeanors.
Second precinct: 9 arrests - there were twice as
many felonies as the first precinct.
1st Precinct : x1 x2 6
2nd Pr ecinct : 2x1 x2 9

35. 11 11
Solution Note: Inverse of
21
is
2 1
11 x1 6
*
21 x2 9
11 11 x1 11 6 Premultiply both sides by
* * * inverse matrix
2 1 21 x2 2 1 9
10 x1 3 A square matrix multiplied by its
* inverse results in the identity matrix.
01 x2 3
x1 3 A 2x2 identity matrix multiplied by
the 2x1 matrix results in the original
x2 3 2x1 matrix.

36. General Form
n equations in n variables:
n
aijxj bi or Ax b
j 1
unknown values of x can be found using the
inverse of matrix A such that
1 1
x A Ax A b

37. Garin-Lowry Model
Ax y x
The object is to find x given A and y . This
is done by solving for x :
y Ix Ax
y (I A)x
1
(I A) y x

38. Matrix Operations in Excel
Select the
cells in
which the
answer
will
appear

39. Matrix Multiplication in Excel
1) Enter
“=mmult(“
2) Select the
cells of the
first matrix
3) Enter comma
“,”
4) Select the
cells of the
second matrix
5) Enter “)”

40. Matrix Multiplication in Excel
Enter these
three
key
strokes
at the
same
time:
control
shift
enter

41. Matrix Inversion in Excel
 Follow the same procedure
 Select cells in which answer is to be
displayed
 Enter the formula: =minverse(
 Select the cells containing the matrix to be
inverted
 Close parenthesis – type “)”
 Press three keys: Control, shift, enter