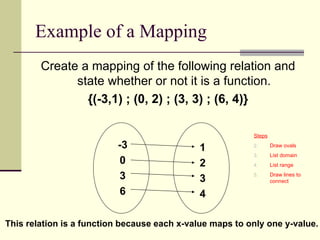
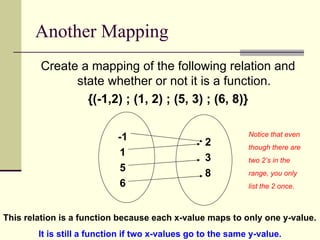
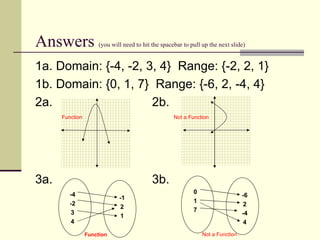
The document defines relations and functions. A relation is a set of ordered pairs, while a function is a special type of relation where each x-value is mapped to only one y-value. The domain is the set of x-values and the range is the set of y-values. Functions can be identified using the vertical line test or by mapping the relation to check if any x-values are mapped to multiple y-values. Evaluating functions involves substituting domain values into the function rule to find the corresponding range values.

1. Relations and Functions .

2. What is a Relation? A relation is a set of ordered pairs. When you group two or more points in a set, it is referred to as a relation. When you want to show that a set of points is a relation you list the points in braces. For example, if I want to show that the points (-3,1) ; (0, 2) ; (3, 3) ; & (6, 4) are a relation, it would be written like this: {(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)} ……… .

3. Domain and Range Each ordered pair has two parts, an x-value and a y-value. The x-values of a given relation are called the Domain . The y-values of the relation are called the Range . When you list the domain and range of relation, you place each the domain and the range in a separate set of braces. ……… .

4. For Example, 1. List the domain and the range of the relation {(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)} Domain: { -3, 0, 3, 6} Range: {1, 2, 3, 4} 2. List the domain and the range of the relation {(-3,3) ; (0, 2) ; (3, 3) ; (6, 4) ; ( 7, 7)} Domain: {-3, 0, 3, 6, 7} Range: {3, 2, 4, 7} Notice! Even though the number 3 is listed twice in the relation, you only note the number once when you list the domain or range! ……… .

5. What is a Function? A function is a relation that assigns each y-value only one x-value. What does that mean? It means, in order for the relation to be considered a function, there cannot be any repeated values in the domain. There are two ways to see if a relation is a function: Vertical Line Test Mappings ……… .

6. Using the Vertical Line Test Use the vertical line test to check if the relation is a function only if the relation is already graphed. Hold a straightedge (pen, ruler, etc) vertical to your graph. Drag the straightedge from left to right on the graph. 3. If the straightedge intersects the graph once in each spot , then it is a function. If the straightedge intersects the graph more than once in any spot, it is not a function. A function! ……… .

7. Examples of the Vertical Line Test function function Not a function Not a function ……… .

8. Mappings If the relation is not graphed, it is easier to use what is called a mapping . When you are creating a mapping of a relation, you draw two ovals. In one oval, list all the domain values. In the other oval, list all the range values. Draw a line connecting the pairs of domain and range values. If any domain value ‘maps’ to two different range values, the relation is not a function. It’s easier than it sounds  ……… .

9. Example of a Mapping Create a mapping of the following relation and state whether or not it is a function. {(-3,1) ; (0, 2) ; (3, 3) ; (6, 4)} Steps Draw ovals List domain List range Draw lines to connect -3 0 3 6 1 2 3 4 This relation is a function because each x-value maps to only one y-value. ……… .

10. Another Mapping Create a mapping of the following relation and state whether or not it is a function. {(-1,2) ; (1, 2) ; (5, 3) ; (6, 8)} -1 1 5 6 2 3 8 Notice that even though there are two 2’s in the range, you only list the 2 once. This relation is a function because each x-value maps to only one y-value. It is still a function if two x-values go to the same y-value. ……… .

11. Last Mapping Create a mapping of the following relation and state whether or not it is a function. {(-4,-1) ; (-4, 0) ; (5, 1) ; (3, 9)} -4 5 3 -1 0 1 9 This relation is NOT a function because the (-4) maps to the (-1) & the (0). It is NOT a function if one x-value go to two different y-values. ……… . Make sure to list the (-4) only once!

12. Vocabulary Review Relation : a set of order pairs. Domain : the x-values in the relation. Range : the y-values in the relation. Function : a relation where each x-value is assigned (maps to) on one y-value. Vertical Line Test : using a vertical straightedge to see if the relation is a function. Mapping : a diagram used to see if the relation is a function. ……… .

13. Practice (you will need to hit the spacebar to pull up the next slide) Complete the following questions and check your answers on the next slide. Identify the domain and range of the following relations: a. {(-4,-1) ; (-2, 2) ; (3, 1) ; (4, 2)} b. {(0,-6) ; (1, 2) ; (7, -4) ; (1, 4)} Graph the following relations and use the vertical line test to see if the relation is a function. Connect the pairs in the order given. a. {(-3,-3) ; (0, 6) ; (3, -3)} b. {(0,6) ; (3, 3) ; (0, 0)} Use a mapping to see if the following relations are functions: a. {(-4,-1) ; (-2, 2) ; (3, 1) ; (4, 2)} b. {(0,-6) ; (1, 2) ; (7, -4) ; (1, 4)}

14. Answers (you will need to hit the spacebar to pull up the next slide) 1a. Domain: {-4, -2, 3, 4} Range: {-2, 2, 1} 1b. Domain: {0, 1, 7} Range: {-6, 2, -4, 4} 2a. 2b. 3a. 3b. Function Not a Function Function Not a Function -4 -2 3 4 -1 2 1 0 1 7 -6 2 -4 4

15. One more thing… The equation that represents a function is called a function rule . A function rule is written with two variables, x and y. It can also be written in function notation , f(x), but we’ll talk about that on Thursday. When you are given a function rule, you can evaluate the function at a given domain value to find the corresponding range value. ……… .

16. How to Evaluate a Function Rule To evaluate a function rule, substitute the value in for x and solve for y. Examples Evaluate the given function rules for x = 2 y= x + 5 y= 2x -1 y= -x + 2 y=(2)+ 5 y= 7 y=2(2)-1 y= 4 – 1 y= 3 y=-(2)+2 y= -2 + 2 y= 0 ……… .

17. Evaluating for a given domain You can also be asked to find the range values for a given domain. This is the same as before, but now you’re evaluating the same function rule for more than one number. The values that you are substituting in are x values, so they are apart of the domain. The values you are generating are y-values, so they are apart of the range. ……… .

18. Example Find the range values of the function for the given domain. y = -3x + 2 ; {-1, 0, 1, 2} y = -3x + 2 y = -3x + 2 y = -3x + 2 y = -3x + 2 y = -3(-1) + 2 y = -3(0) + 2 y = -3(1) + 2 y = -3(2) + 2 y = 3 + 2 y = 0 + 2 y = -3 + 2 y = -6 +2 y = 5 y = 2 y = -1 y = -4 The range values for the given domain are { 5, 2, -1, -4}. ……… . Steps Sub in each domain value in one @ a time. Solve for y in each List y values in braces.

19. One more example Find the range values of the function for the given domain. y = 5x - 7 ; {-3, -2, 4} y = 5x -7 y = 5x -7 y = 5x - 7 y = 5(-3) - 7 y= 5(-2) -7 y = 5(4) - 7 y = -15 - 7 y= -10 - 7 y= 20 - 7 y= -22 y= -17 y= 13 The range values for the given domain are { -22, -17, 13}. ……… .

20. Practice (you’ll need to hit the spacebar to pull up the next slide) 1. Find the range values of the function for the given domain. y = 3x + 1 ; {-4, 0, 2} 2. Find the range values of the function for the given domain. y = -2x + 3 ; {-5, -2, 6} Steps Sub in each domain value in one @ a time. Solve for y in each List y values in braces.

21. Answers 1. 2. y = 3x + 1 y = 3(-4) + 1 y = -12 + 1 y = -11 y = 3x + 1 y = 3(0) + 1 y = 0 + 1 y = 1 Ans. { -11, 1, 7} y = 3x + 1 y = 3(2) + 1 y = 6 + 1 y = 7 y = -2x + 3 y = -2(-5) + 3 y = 10 + 3 y = 13 y = -2x + 3 y = -2(-2) + 3 y = 4 +3 y = 7 Ans. { 13, 7, -9} y = -2x + 3 y = -2(6) + 3 y = -12 +3 y = -9