Download to read offline
![The m × n zero matrix, denoted 0, is the m × n
matrix whose elements are all zeros.
( ) 00
0)(
0
=
=−+
=+
A
AA
AA
00
00
[ ]000
2 × 2
1 × 3](https://image.slidesharecdn.com/1563-matrixalgebra-161031144110/75/1563-matrix-algebra-5-2048.jpg)
Uploaded byDr Fereidoun Dejahang
1563 matrix algebra
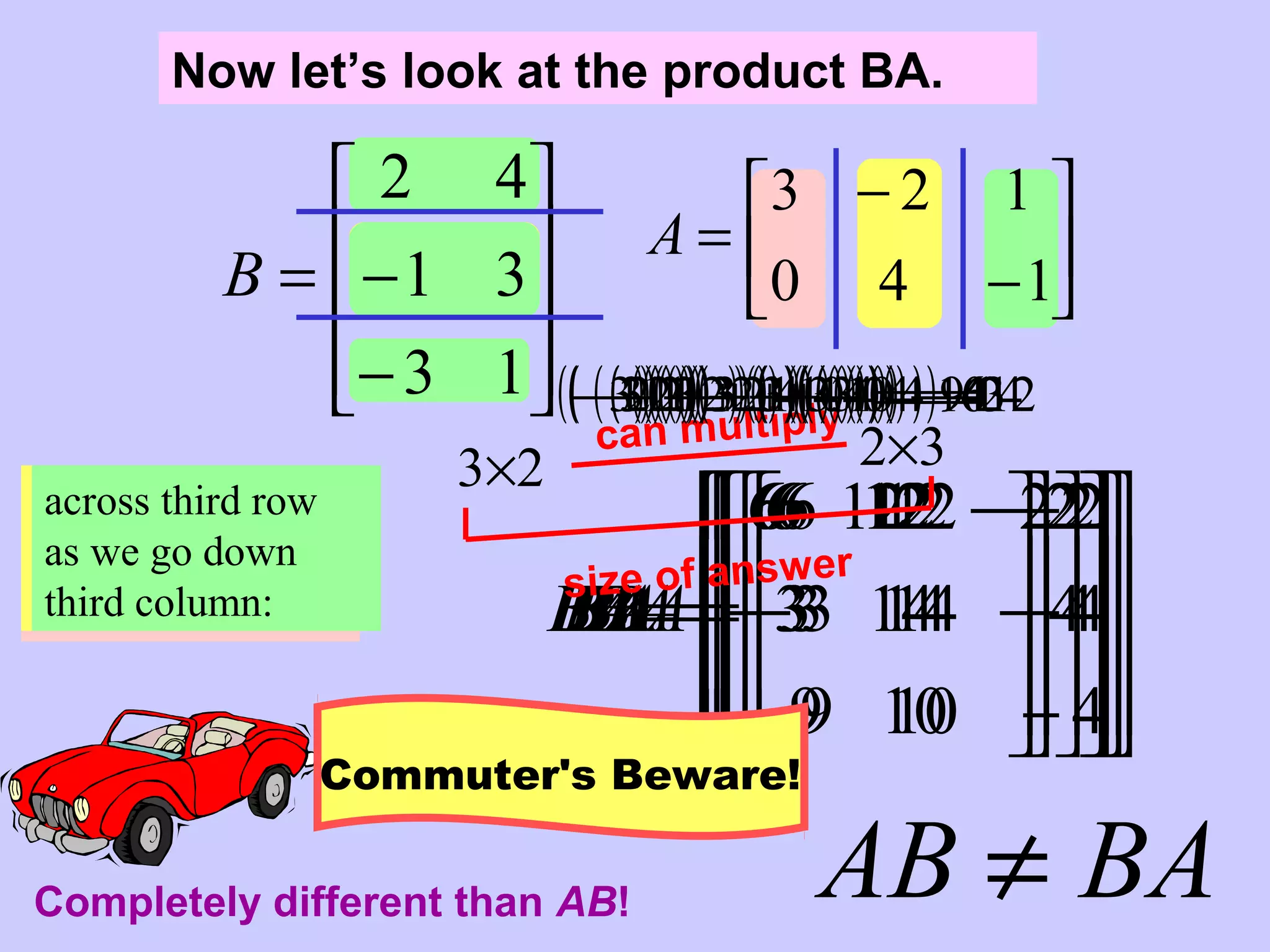
The document discusses fundamental operations for matrices, including addition, scalar multiplication, and multiplication of matrices, while explaining the required dimensions for these operations. It also covers properties of matrix multiplication and the process of finding the inverse of a matrix. Additionally, it illustrates how matrix operations can be used to solve systems of equations.
More Related Content
![Metrix[1]](https://cdn.slidesharecdn.com/ss_thumbnails/metrix1-140722104749-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
![MATH 564 Advanced Mathematics for Data Science[1].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/math564advancedmathematicsfordatascience1-250915112031-c023a536-thumbnail.jpg?width=640&height=640&fit=bounds)
1563 matrix algebra
- 2. If A andB are both m × n matrices then the sum of A and B, denoted A + B, is a matrix obtained by adding corresponding elements of A and B. − − = 310 221 A − − = 412 403 B − =+ 2 BA If A and B are both m × n matrices then the sum of A and B, denoted A + B, is a matrix obtained by adding corresponding elements of A and B. add these − − = 310 221 A − − = 412 403 B −− =+ 22 BA add these − − = 310 221 A − − = 412 403 B −− =+ 622 BA add these − − = 310 221 A − − = 412 403 B −− =+ 2 622 BA add these − − = 310 221 A − − = 412 403 B −− =+ 02 622 BA add these − − = 310 221 A − − = 412 403 B − −− =+ 102 622 BA add these
- 3.
- 4. If A isan m × n matrix and s is a scalar, then we let kA denote the matrix obtained by multiplying every element of A by k. This procedure is called scalar multiplication. ( ) ( ) ( ) ( ) k hA kh A k h A kA hA k A B kA kB = + = + + = + − − = 310 221 A ( ) ( ) ( ) ( ) ( ) ( ) − − = − − = 930 663 331303 232313 3A PROPERTIES OF SCALAR MULTIPLICATION
- 5. The m ×n zero matrix, denoted 0, is the m × n matrix whose elements are all zeros. ( ) 00 0)( 0 = =−+ =+ A AA AA 00 00 [ ]000 2 × 2 1 × 3
- 6. The multiplication ofmatrices is easier shown than put into words. You multiply the rows of the first matrix with the columns of the second adding products − − = 140 123 A − −= 13 31 42 B Find AB First we multiply across the first row and down the first column adding products. We put the answer in the first row, first column of the answer. ( )23( ) ( )( )1223 −−+( )( ) ( )( ) ( )( ) 5311223 =−+−−+
- 7. − − = 140 123 A − −= 13 31 42 B Find AB We multipliedacross first row and down first column so we put the answer in the first row, first column. = 5 AB Now we multiply across the first row and down the second column and we’ll put the answer in the first row, second column. ( )( )43( )( ) ( )( )3243 −+( )( ) ( )( ) ( )( ) 7113243 =+−+ = 75 AB Now we multiply across the second row and down the first column and we’ll put the answer in the second row, first column. ( )( )20( )( ) ( )( )1420 −+( )( ) ( )( ) ( )( ) 1311420 −=−−+−+ − = 1 75 AB Now we multiply across the second row and down the second column and we’ll put the answer in the second row, second column. ( )( )40( )( ) ( )( )3440 +( )( ) ( )( ) ( )( ) 11113440 =−++ − = 111 75 AB Notice the sizes of A and B and the size of the product AB.
- 8. To multiply matricesA and B look at their dimensions pnnm ×× MUST BE SAME SIZE OF PRODUCT If the number of columns of A does not equal the number of rows of B then the product AB is undefined.
- 9. = 6 BA = 126 BA − = 2126 BA − − = 3 2126 BA − − =143 2126 BA −− − = 4143 2126 BA − −− − = 9 4143 2126 BA − −− − = 109 4143 2126 BA −− −− − = 4109 4143 2126 BA Now let’s look at the product BA. − −= 13 31 42 B − − = 140 123 A BAAB ≠ 2×33×2 can multiply size of answer across first row as we go down first column: ( )( ) ( )( ) 60432 =+ across first row as we go down second column: ( )( ) ( )( ) 124422 =+− across first row as we go down third column: ( )( ) ( )( ) 21412 −=−+ across second row as we go down first column: ( )( ) ( )( ) 30331 −=+− across second row as we go down second column: ( )( ) ( )( ) 144321 =+−− across second row as we go down third column: ( )( ) ( )( ) 41311 −=−+− across third row as we go down first column: ( )( ) ( )( ) 90133 −=+− across third row as we go down second column: ( )( ) ( )( ) 104123 =+−− across third row as we go down third column: ( )( ) ( )( ) 41113 −=−+− Completely different than AB! Commuter's Beware!
- 10. ( ) () ( ) ( ) BCACCBA ACABCBA CABBCA +=+ +=+ = PROPERTIES OF MATRIX MULTIPLICATION BAAB ≠ Is it possible for AB = BA ?,yes it is possible.
- 11. an n ×n matrix with ones on the main diagonal and zeros elsewhere = 100 010 001 3I What is AI? What is IA? − − = 322 510 212 A = 100 010 001 3I A= − − 322 510 212 A= − − 322 510 212 Multiplying a matrix by the identity gives the matrix back again.
- 12. = −− 10 01 24 13 ? Let Abe an n× n matrix. If there exists a matrix B such that AB = BA = I then we call this matrix the inverse of A and denote it A-1 . −− 2 3 2 2 1 1 = −− −− 10 01 24 13 2 3 2 2 1 1 Can we find a matrix to multiply the first matrix by to get the identity?
- 13. If A hasan inverse we say that A is nonsingular. If A-1 does not exist we say A is singular. To find the inverse of a matrix we put the matrix A, a line and then the identity matrix. We then perform row operations on matrix A to turn it into the identity. We carry the row operations across and the right hand side will turn into the inverse. To find the inverse of a matrix we put the matrix A, a line and then the identity matrix. We then perform row operations on matrix A to turn it into the identity. We carry the row operations across and the right hand side will turn into the inverse. −− = 72 31 A − 1210 0131 2r1+r2 −− 1072 0131 −− 1210 0131 −r2 −− 1210 3701r1 − r2
- 14. −− = 72 31 A −− =− 12 371 A Check thisanswer by multiplying. We should get the identity matrix if we’ve found the inverse. =− 10 011 AA
- 15. We can useA-1 to solve a system of equations 352 13 =+ =+ yx yx bx =A To see how, we can re-write a system of equations as matrices. coefficient matrix variable matrix constant matrix 52 31 y x = 3 1
- 16. bx 1− = A bx11 −− = AAA bx =A left multiply both sides by the inverse of A This is just the identity bx 1− = AI but the identity times a matrix just gives us back the matrix so we have:This then gives us a formula for finding the variable matrix: Multiply A inverse by the constants.
- 17. 352 13 =+ =+ yx yx = 52 31 A find theinverse 1052 0131 −− 1210 0131 -2r1+r2 −1210 0131 -r2 − − 1210 3501r1-3r2 − = − − =− 1 4 3 1 12 351 bA This is the answer to the system x y
- 18. Your calculator cancompute inverses and determinants of matrices. To find out how, refer to the manual or click here to check out the website.
- 19. Acknowledgement I wish tothank Shawna Haider from Salt Lake Community College, Utah USA for her hard work in creating this PowerPoint. www.slcc.edu Shawna has kindly given permission for this resource to be downloaded from www.mathxtc.com and for it to be modified to suit the Western Australian Mathematics Curriculum. Stephen Corcoran Head of Mathematics St Stephen’s School – Carramar www.ststephens.wa.edu.au