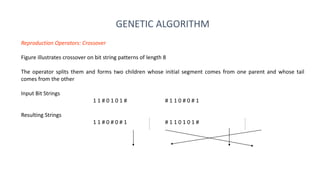
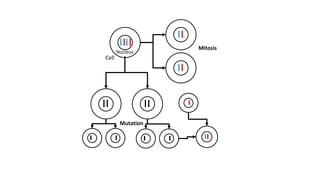
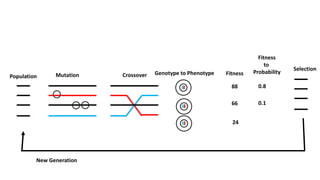
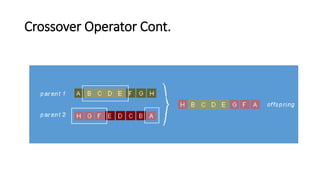
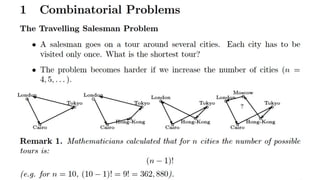
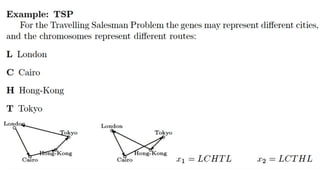
Genetic algorithms (GAs) are optimization algorithms inspired by Darwinian evolution. They use techniques like mutation, crossover, and selection to evolve solutions to problems iteratively. The document provides examples to illustrate how GAs work, including finding a binary number and fitting a polynomial to data points. GAs initialize a population of random solutions, then improve it over generations by keeping the fittest solutions and breeding them using crossover and mutation to produce new solutions, until finding an optimal or near-optimal solution.

1. Genetic Algorithm

2. What is Genetic Algorithms?
Genetic Algorithms (GAs) are adaptive heuristic search algorithm based
on the evolutionary ideas of natural selection and genetics. As such
they represent an intelligent exploitation of a random search used to
solve optimization problems. Although randomised, GAs are by no
means random, instead they exploit historical information to direct the
search into the region of better performance within the search space.
The basic techniques of the GAs are designed to simulate processes in
natural systems necessary for evolution, specially those follow the
principles first laid down by Charles Darwin of "survival of the fittest.".
Since in nature, competition among individuals for scanty resources
results in the fittest individuals dominating over the weaker ones.

3. Why Genetic Algorithms?
It is better than conventional AI in that it is more robust. Unlike older AI
systems, they do not break easily even if the inputs changed slightly, or
in the presence of reasonable noise. Also, in searching a large state-
space, multi-modal state-space, or n-dimensional surface, a genetic
algorithm may offer significant benefits over more typical search of
optimization techniques. (linear programming, heuristic, depth-first,
breath-first, and praxis.)

4. Genetic Algorithms Overview
GAs simulate the survival of the fittest among individuals over consecutive
generation for solving a problem. Each generation consists of a population of
character strings that are analogous to the chromosome that we see in our DNA.
Each individual represents a point in a search space and a possible solution. The
individuals in the population are then made to go through a process of evolution.
GAs are based on an analogy with the genetic structure and behaviour of
chromosomes within a population of individuals using the following foundations:
• Individuals in a population compete for resources and mates.
• Those individuals most successful in each 'competition' will produce more offspring than
those individuals that perform poorly.
• Genes from `good' individuals propagate throughout the population so that two good parents
will sometimes produce offspring that are better than either parent.
• Thus each successive generation will become more suited to their environment.

5. Cell
Nucleus
Mitosis
Mutation

6. Population Mutation Crossover Genotype to Phenotype Fitness
88
66
24
Fitness
to
Probability
0.8
0.1
Selection
New Generation

7. Implementation Details
After an initial population is randomly generated, the algorithm evolves
the through three operators:
• selection which equates to survival of the fittest;
• crossover which represents mating between individuals;
• mutation which introduces random modifications.

8. 1. Selection Operator
• key idea: give preference to better individuals, allowing them to pass
on their genes to the next generation.
• The goodness of each individual depends on its fitness.
• Fitness may be determined by an objective function or by a subjective
judgement.

9. 2. Crossover Operator
• Prime distinguished factor of GA from other optimization techniques
• Two individuals are chosen from the population using the selection
operator
• A crossover site along the bit strings is randomly chosen
• The values of the two strings are exchanged up to this point
• If S1=000000 and s2=111111 and the crossover point is 2 then S1'=110000
and s2'=001111
• The two new offspring created from this mating are put into the next
generation of the population
• By recombining portions of good individuals, this process is likely to create
even better individuals

10. Crossover Operator Cont.

11. 3. Mutation Operator
• With some low probability, a portion of the new individuals will have
some of their bits flipped.
• Its purpose is to maintain diversity within the population and inhibit
premature convergence.
• Mutation alone induces a random walk through the search space
• Mutation and selection (without crossover) create a parallel, noise-
tolerant, hill-climbing algorithms

12. Effects of Genetic Operators
• Using selection alone will tend to fill the population with copies of the
best individual from the population
• Using selection and crossover operators will tend to cause the
algorithms to converge on a good but sub-optimal solution
• Using mutation alone induces a random walk through the search
space.
• Using selection and mutation creates a parallel, noise-tolerant, hill
climbing algorithm

13. The Algorithms
1. randomly initialize population(t)
2. determine fitness of population(t)
3. repeat
1. select parents from population(t)
2. perform crossover on parents creating population(t+1)
3. perform mutation of population(t+1)
4. determine fitness of population(t+1)
4. until best individual is good enough

14. Genetics Algorithm

19. GENETIC ALGORITHM
Evaluation/Fitness Function
It is used to determine the fitness of a chromosome
Creating a good fitness function is one of the challenging tasks of using GA

20. Fitness Function
The fitness function can be the score of the classification accuracy of the rule-set over a set of provided training
examples
Often other criteria may be included as well, such as the complexity of the rules or the size of the rule set
GENETIC ALGORITHM

23. (Probability)

29. • Two-point crossover at point 3 and 5
P1 = 101 00 10 = O1 = 101 10 10
P2 = 011 10 01 O2 = 011 00 01

31. Artificial Intelligence (Genetic Algorithm)

32. 32
Simple example
• Suppose your “organisms” are 32-bit computer words
• You want a string in which all the bits are ones
• Here’s how you can do it:
• Create 100 randomly generated computer words
• Repeatedly do the following:
• Count the 1 bits in each word
• Exit if any of the words have all 32 bits set to 1
• Keep the ten words that have the most 1s (discard the rest)
• From each word, generate 9 new words as follows:
• Pick a random bit in the word and toggle (change) it
• Note that this procedure does not guarantee that the next “generation” will
have more 1 bits, but it’s likely

33. Realistic Example
• Suppose you have a large number of (x, y) data points
• For example, (1, 4), (3, 9), (5, 8), ...
• You would like to fit a polynomial (of up to degree 1) through these data points
• That is, you want a formula y = mx + c that gives you a reasonably good fit to the actual data
• Here’s the usual way to compute goodness of fit:
• Compute the sum of (actual y – predicted y)2 for all the data points
• The lowest sum represents the best fit
• You can use a genetic algorithm to find a “pretty good” solution

34. Realistic Example
• Your formula is y = mx + c
• Your unknowns are m and c; where m and c are integers
• Your representation is the array [m, c]
• Your evaluation function for one array is:
• For every actual data point (x, y)
• Compute ý = mx + c
• Find the sum of (y – ý)2 over all x
• The sum is your measure of “badness” (larger numbers are worse)
• Example: For [m,c] = [5, 7] and the data points (1, 10) and (2, 13):
• ý = 5x + 7 = 12 when x is 1
• ý = 5x + 7 = 17 when x is 2
• Now compute the badness
(10 - 12)2 + (13 – 17)2 = 22 + 42 = 20
• If these are the only two data points, the “badness” of [5, 7] is 20

35. Realistic Example
• Your GA might be as follows:
• Create two-element arrays of random numbers
• Repeat 50 times (or any other number):
• For each of the arrays, compute its badness (using all data points)
• Keep the best arrays (with low badness)
• From the arrays you keep, generate new arrays as follows:
• Convert the numbers in the array to binary, toggle one of the bits at random
• Quit if the badness of any of the solution is zero
• After all 50 trials, pick the best array as your final answer

36. Realistic Example
• (x, y) : {(1,5) (3, 9)}
• [2 7][1 3] (initial random population, where m and c represent genes)
• ý = 2x + 7 = 9 when x is 1
• ý = 2x + 7 = 13 when x is 3
• Badness: (5 – 9)2 + (9 – 13)2 = 42 + 42 = 32
• ý = 1x + 3 = 4 when x is 1
• ý = 1x + 3 = 6 when x is 3
• Badness: (5 – 4)2 + (9 – 6)2 = 12 + 32 = 10
• Now, lets keep the one with low “badness” [1 3]
• Binary representation [001 011]
• Apply mutation to generate new arrays [011 011]
• Now we have [1 3] [3 3] as the new population considering that we keep the two best individuals

37. Realistic Example
• (x, y) : {(1,5) (3, 9)}
• [1 3][3 3] (current population)
• ý = 1x + 3 = 4 when x is 1
• ý = 1x + 3 = 6 when x is 3
• Badness: (5 – 4)2 + (9 – 6)2 = 1 + 9 = 10
• ý = 3x + 3 = 6 when x is 1
• ý = 3x + 3 = 12 when x is 3
• Badness: (5 – 6)2 + (9 – 12)2 = 1 + 9 = 10
• Lets keep the [3 3]
• Representation [011 011]
• Apply mutation to generate new arrays [010 011] i.e. [2,3]
• Now we have [3 3] [2 3] as the new population

38. Realistic Example
• (x, y) : {(1,5) (3, 9)}
• [3 3][2 3] (current population)
• ý = 3x + 3 = 6 when x is 1
• ý = 3x + 3 = 12 when x is 3
• Badness: (5 – 6)2 + (9 – 12)2 = 1 + 9 = 10
• ý = 2x + 3 = 5 when x is 1
• ý = 2x + 3 = 9 when x is 3
• Badness: (5 – 5)2 + (9 – 9)2 = 02 + 02 = 0
• Solution found [2 3]
• y = 2x+3
• Note: It is not necessary that the badness must always be zero. It can be some other threshold value as
well.

39. GENETIC ALGORITHM
Reproduction Operators: Crossover
Crossover operation takes two candidate solutions and divides them, swapping components to produce two new
candidates

40. GENETIC ALGORITHM
Reproduction Operators: Crossover
Figure illustrates crossover on bit string patterns of length 8
The operator splits them and forms two children whose initial segment comes from one parent and whose tail
comes from the other
Input Bit Strings
1 1 # 0 1 0 1 # # 1 1 0 # 0 # 1
Resulting Strings
1 1 # 0 # 0 # 1 # 1 1 0 1 0 1 #

41. GENETIC ALGORITHM
Reproduction Operators: Crossover
The place of split in the candidate solution is an arbitrary choice. This split may be at any point in the solution
This splitting point may be randomly chosen or changed systematically during the solution process
Crossover can unite an individual that is doing well in one dimension with another individual that is doing well in
the other dimension

42. GENETIC ALGORITHM
Reproduction Operators: Crossover
Two types: Single point crossover & Uniform crossover
Single type crossover
This operator takes two parents and randomly selects a single point between two genes to cut both
chromosomes into two parts (this point is called cut point)
The first part of the first parent is combined with the second part of the second parent to create the first child
The first part of the second parent is combined with the second part of first parent to create the second child
1000010 1000001
1110001 1110010

43. GENETIC ALGORITHM
Reproduction Operators: Crossover
Uniform crossover
The value of each gene of an offspring’s chromosome is randomly taken from either parent
This is equivalent to multiple point crossover
1000010
1110001 1010010

44. 44
GENETIC ALGORITHM
Example
Find a number: 001010
You have guessed this binary number. If you write a program to find it, then there are 26 = 64 possibilities
If you find it with the help of Genetic Algorithm, then the program gives a number and you tell its fitness
The fitness score is the number of correctly guessed bits

45. 45
GENETIC ALGORITHM
Example
Find a number: 001010
Step 1. Chromosomes produced.
A) 010101 - 1
B) 111101 - 1
C) 011011 - 4 *
D) 101100 - 3 *
Best ones C & D

46. 46
GENETIC ALGORITHM
Example
Find a number: 001010
Mating New Variants Evaluation
C) 01:1011 01:1100 (E) 3
D) 10:1100 10:1011 (F) 4 *
C) 0110:11 0110:00 (G) 4 *
D) 1011:00 1011:11 (H) 3
Selection of F & G

47. 47
GENETIC ALGORITHM
Example
Mating New Variants Evaluation
F) 1:01011 1:11000 (H) 3
G) 0:11000 0:01011 (I) 5 *
F) 101:011 101:000 (J) 4 *
G) 011:000 011:011 (K) 4
Selection of I and J

48. 48
GENETIC ALGORITHM
Example
Mating New Variants Evaluation
I) 0010:11 0010:00 (L) 5
J) 1010:00 1010:11 (M) 4
I) 00101:1 00101:0 (N) 6 (success) *
J) 10100:0 10100:1 (O) 3
In this game success was achieved after 16 questions, which is 4 times faster then checking all possible 26 = 64
combination

49. 49
GENETIC ALGORITHM
Example
Mutation was not used in this example. Mutation would have been necessary, if, e.g. there was a 0 in the third bit of
all 3 initial individuals. In that case no matter how the individuals are combined, we can never change this bit into 1.
Mutation takes evolution out of a dead end.