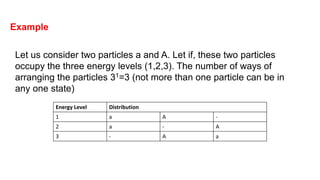
The document discusses three types of statistics that describe different physical situations: Maxwell-Boltzmann, Bose-Einstein, and Fermi-Dirac statistics. It outlines the characteristics, equations, and examples of each type, including the roles of distinguishability and energy occupancy rules for particles. Additionally, it touches on concepts such as Fermi energy and the derivation of the Fermi-Dirac and Bose-Einstein distribution laws.

1. Dr. Anjali Devi JS
Contract Faculty, Mahatma Gandhi University, Kottayam, Kerala
Classical & Quantum Statistics

2. Types of Statistics
Different physical situation encountered in nature are
described by three types of statistics:
(1) Maxwell-Boltzmann (or M-B) statistics
(2) Bose-Einstein (or B-E) statistics
(3) Fermi Dirac Statistics
(Classical
Statistics)
(Quantum
Statistics)

3. (1) Maxwell-Boltzmann (or M-B) statistics
 Particles are assumed to be distinguishable.
 Any number of particles may occupy the same energy level.
 Particles obeying M-B statistics are called boltzons or maxwellons.
 Example: Molecules of a gas.

4. (2) Bose-Einstein (or B-E) statistics
 Particles are indistinguishable.
 Any number of particles may occupy the same energy level.
 Particles obeying B-E statistics are called bosons.
 These particles have integral spin.
 Example: hydrogen (H2), deuterium (D2), nitrogen (N2), helium-4 (He4),
photons.

5. (3) Fermi-Dirac (or F-D) statistics
 Particles are indistinguishable.
 But only one particle may occupy a given energy level.
 These particles have half-integral spin.
 Particles obeying F-D statistics are called fermions.
 Example: protons, electrons, helium-3, and nitric oxide (NO).

6. Fermions are those species whose wave functions are anti-
symmetric with respect to the exchange of particles .
Bosons are those species whose wave functions are symmetric with
respect to the exchange of particles .

7. Maxwell Boltzmann Statistics (classical law)
This law states that, the total fixed amount of energy is distributed
among various members of an assembly of identical particles.
𝜀0
𝜀1
𝜀2 Instantaneous configuration
of the system [5,0,0]
A general configuration [N0,N1,N2..] can be achieved in W
different ways, where W is called weight of the configuration.
W=
𝑁!
𝑁0!𝑁1!𝑁2!….

8. Question
Calculate the weight of the configuration in which 20 objects are
distributed in the arrangement 0, 1,5, 0, 8,0,3,2,0,1
Configuration =[0,1,5,0,8,0,3,2,0,1]
N =0+1+5+0+8+0+3+2+0+1= 20
Answer: 4.19 × 1010
W=
𝑁!
𝑁0!𝑁1!𝑁2!….

9. Boltzmann Distribution Law
The Maxwell Boltzmann law
The number of particles in the configuration of greatest weight (i.e.,
most probable distribution for a microstate) depends on energy of
the state by 𝑁𝑖 =
𝑔𝑖
𝑒(𝛼+𝛽𝜀𝑖)
For the search of maximum value of W (i.e., configuration in the
greatest weight), we must also ensure that configuration also
satisfies the condition:
Constant total energy: 𝑖 𝑁𝑖𝜀𝑖 = 𝐸
Constant total number of molecules: 𝑖 𝑁𝑖 = 𝑁
𝑔𝑖-degeneracy,
𝛼, 𝛽- Undetermined multipliers

10. 𝛼 =
−𝐸𝐹
𝑘𝑇 𝛽 =
1
𝑘𝑇
𝑘-Boltzmann constant,
T-Absolute temperature
EF
- Fermi Energy
𝜶, 𝜷- Undetermined multipliers

11. Concepts
Fermi Level: The term used to describe the top of the collection of
electron energy levels at absolute zero temperature.
Electrons are Fermions and by Pauli exclusion principle cannot exist
in identical energy states.
Fermi Energy: This is the maximum energy that an electron can
have in a conductor at 0K. It is given by,
𝐸𝐹 =
1
2
𝑚𝑣𝐹
2
Where 𝑣𝐹 is the velocity of electron at Fermi level.

12. Fermi Dirac Distribution-Derivation
W=
𝑔𝑖!
𝑔𝑖−𝑔𝑖𝑓𝑖 !𝑔𝑖𝑓𝑖!
𝑔𝑖- Degeneracy, 𝑓𝑖 -probability of occupying a state at energy 𝜀𝑖
The number of possible ways- called configurations-to fit 𝑔𝑖𝑓𝑖 electrons in
𝑔𝑖states, given the restriction that only one electron in 𝑔𝑖 states, given the
restriction that only one electron can occupy each state, equals:

13. This equation is obtained by numbering the individual states and
exchanging the states rather than the electrons. This yields a total
number of 𝑔𝑖 possible configurations. However the empty states are all
identical, we need to divide by the number of permutations between
the empty states, as all permutations cannot be distinguished and can
therefore only be counted once. In addition, all the filled states are
indistinguishable from each other, so we need to divide also by
permutations between the filled states namely 𝑔𝑖𝑓𝑖!
Fermi Dirac Distribution-Derivation

14. Multiplicity function
 The number of possible ways to fit the electrons in
the number of available states is called the
multiplicity function.
 The multiplicity function for the whole system is the
product of the multiplicity functions for each energy 𝜀𝑖
Fermi Dirac Distribution-Derivation

15. Fermi Dirac Distribution-Derivation
Using Stirling’s approximation, one can eliminate the
factorial signs, yielding:
ln 𝑊 = 𝑖 ln 𝑊𝑖 = 𝑖 [𝑔𝑖ln 𝑔𝑖 − 𝑔𝑖 1 − 𝑓𝑖 𝑙𝑛(𝑔𝑖−𝑔𝑖𝑓𝑖) − 𝑔𝑖𝑓𝑖𝑙𝑛𝑔𝑖𝑓𝑖]
The total number of particles =N
The total energy of these N electrons = E
These system parameters are related to the number of states at
each energy, 𝑔𝑖 and the probability of occupancy of each state, 𝑓𝑖,
by:
N= 𝑖 𝑔𝑖𝑓𝑖 E= 𝑖 𝜀𝑖𝑔𝑖𝑓𝑖

16. According to basic assumption of statistical thermodynamics, all
possible configurations are equally probable. The multiplicity function
provides the number of configurations for a specific set of occupancy
probabilities, 𝑓𝑖. The multiplicity function sharply peaks the thermal
equilibrium distribution. The occupancy probability in thermal
equilibrium is therefore obtained by finding the maximum of the
multiplicity function, W, while keeping the total energy and the
number of electrons constant.
Maximise logarithm of multiplicity function using Lagrange method:
ln W-𝑎 𝑗 𝑔𝑗𝑓𝑗 − 𝑏 𝑗 𝜀𝑗𝑔𝑗
Fermi Dirac Distribution-Derivation

17. The number of particles in the configuration of greatest weight (i.e.,
most probable distribution for a microstate) depends on energy of
the state by 𝑁𝑖 =
𝑔𝑖
𝑒(𝛼+𝛽𝜀𝑖)+1
𝑔𝑖-degeneracy,
𝛼, 𝛽- Undetermined multipliers
Fermi Dirac Distribution
Law

18. Example
Let us consider two particles a and A. Let if, these two particles
occupy the three energy levels (1,2,3). The number of ways of
arranging the particles 31=3 (not more than one particle can be in
any one state)
Energy Level Distribution
1 a A -
2 a - A
3 - A a

19. Bose Einstein Distribution Law
 Applies to a weakly interacting gas of indistinguishable
bosons with:
 Each group 𝑖 has 𝑔𝑖 𝑠𝑡𝑎𝑡𝑒𝑠, 𝑔𝑖-1 possible subgroups, 𝑁𝑖 to
be shared between them.
Constant total energy: 𝑖 𝑁𝑖𝜀𝑖 = 𝐸
Constant total number of molecules: 𝑖 𝑁𝑖 = 𝑁
 No Pauli Exclusion Principle:𝑁𝑖 ≥ 0, 𝑢𝑛𝑙𝑖𝑚𝑖𝑡𝑒𝑑

20.  Each group 𝑖 has 𝑔𝑖 𝑠𝑡𝑎𝑡𝑒𝑠, 𝑔𝑖-1 possible subgroups, 𝑁𝑖 to
be shared between them.
 Number of combination to do this is:
𝑁𝑖 + 𝑔𝑖 − 1 !
𝑁𝑖! 𝑔𝑖 − 1 !
 The number of microstates in distribution Ni states
𝑊 =
𝑖
𝑁𝑖 + 𝑔𝑖 − 1 !
𝑁𝑖! 𝑔𝑖 − 1 !
Bose Einstein Distribution Law

21. The number of particles in the configuration of greatest weight (i.e.,
most probable distribution for a microstate) depends on energy of
the state by 𝑁𝑖 =
𝑔𝑖
𝑒(𝛼+𝛽𝜀𝑖)−1
𝑔𝑖-degeneracy,
𝛼, 𝛽- Undetermined multipliers
Bose Einstein Distribution Law