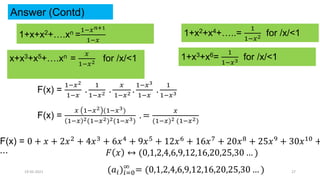
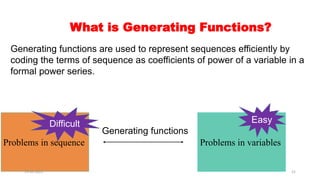
Combinatorics is a subfield of discrete mathematics that focuses on counting combinations and arrangements of discrete objects. It involves counting the number of ways to put things together into various combinations. Some key rules in combinatorics include the sum rule, which states that the number of ways to accomplish either of two independent tasks is the sum of the number of ways to accomplish each task individually. The product rule states that the number of ways to accomplish two independent tasks is the product of the number of ways to accomplish each task. Generating functions can be used to efficiently represent counting sequences by coding terms as coefficients of a variable in a formal power series. They allow problems involving counting and arrangements to be solved using operations with formal power series.

1. Combinatorics
Dr. Anjali Devi J S
Guest Faculty
School of Chemical Sciences
M G University
19-05-2021 1

2. What is Combinatorics?
 A subfield of Discrete mathematics.
 Focus on combination and arrangement of
discrete objects.
 Of being Counting.
19-05-2021 2

3.  Count the no of ways to put things together into various
combinations.
What is Combinatorics?
1
2
3
4
19-05-2021 3

4. Combinatorics- Rules
Sum rule
Task 1 Task 2
Task 1 & Task 2 are independent of each other
m ways to
accomplish
task 1
n ways to
accomplish
task 2
The number of ways that either task 1 or task 2 can be done, but not both
is m+n
19-05-2021 4

5. Question
Mary and Peter are planning to have no more than three children.
What are the possible combinations of girls and boys they might end
up with, if we are not keeping track of the order of the children
Cases No of ways
Having no child 1
They have one child (either boy or
girl)
2
They have 2 children (no of girl be 0,
1, or 2)
3
They have 3 children (no of girls be
0,1,2 or 3)
4
Total no of combination =1+2+3+4= 10
19-05-2021 5

6. Combinatorics- Rules
Product Rule
Task 1 Task 2
Task 1 & Task 2 are independent of each other
m ways to
accomplish
task 1
n ways to
accomplish
task 2
The number of ways that both task 1 and 2 can be done is mn
19-05-2021 6

7. Question
Kyle wants to buy coffee from a coffee shop that sells 4 varieties and
3 size. How many choices of coffee are there in total?
Small Medium Large
Latte Small Latte Medium Latte Large Latte
Mocha Small Mocha Medium Mocha Large
Mocha
Espresso Small Espresso Medium Espresso Large
Espresso
Cappuccino Small
Cappuccino
Medium Cappuccino Large
Cappuccino
Total no of combination =4X3= 12
19-05-2021 7

8. Combinations- Basic rule
If there are totally n objects available, and if we want to choose r at a
time, then the total number of different combinations is given by,
nCr =
𝑛!
𝑛 − 𝑟 ! (𝑟)!
Note: Order of selection does not matter.
19-05-2021 8

9. Question
From a basket of six fruits, how many ways we can choose three
(distinct) fruits at a time to make a fruit salad?
Total 6 fruits are available
n=6
To make fruit salad, we need 3 fruits at a time
r=6
nCr =
𝑛!
𝑛−𝑟 !(𝑟)!
=
6!
6−3 !(3)!
=
6!
3 !(3)!
=
1𝑥2𝑥3𝑥4𝑥5𝑥6
1𝑥2𝑥3 (1𝑥2𝑥3)
= 20
There are 20 different ways.
19-05-2021 9

10. Permutations - Basic Rule
If there are totally n objects available, and if we want to choose r at a
time in a given order, then the total number of different combinations is
given by,
nPr =
𝑛!
𝑛 − 𝑟 !
Note: Order of selection is important.
Permutation is
ordering (rearranging)
of number of distinct
items in a line.
19-05-2021 10

11. Question
Ten athletes are competing for Olympic medal in womens speed
skating (1000 meters). In how many ways might the medal end up
being awarded ?
Total 10 athletes
n=10
There are three medals: gold, silver, bronze
r=3
nPr =
𝑛!
𝑛−𝑟 !
=
10!
10−3 !
=
10!
7 !
=
1𝑥2𝑥3𝑥4𝑥5𝑥6𝑥7𝑥8𝑥9𝑥10
1𝑥2𝑥3𝑥4𝑥5𝑥6𝑥7
= 720
19-05-2021 11

12. Derangements: Solving Problem by Counting
(certain types of) Permutations
A function f has a fixed point x if f(x) =x. This is also the case of
permutations.
x
f(x)
1
5 2
2 3
7 3
4 5 6 7
8 4 1
8 9
6 9
x
f(x)
1
3
3
6 2
4 5 6 7
8 5 1
8
9
A permutation without fixed point is derangement.
2
1
9
4
Derangement-
permutation of the
element of certain
set in a way that no
element of the set
appears in their
original position.
19-05-2021 12

13. Derangements
The arrangement of 6 people in 6 seats can be done in 6! ways. Now in
how many ways can you arrange them again such that none of them are
occupying their original position?
Question
Answer
Derangement value of 6
1 2 3 4 5 6
19-05-2021 13

14. Derangements
Inserting Letters into their respective envelopes
Question
Answer
Case 1: Consider 1 letter L1 and one envelope E1.
In how many ways can the letter be put into a wrong envelope?
There is no way!
L1 E1
19-05-2021 14

15. Derangements
Inserting Letters into their respective envelopes
Question
Answer
Case 2: Consider two letters L1 & L2and their corresponding envelope
E1 & E2
In how many ways can the letter be put into a wrong envelope?
There is only one way!
L1 E1
L2 E2
19-05-2021 15

16. Derangements
Inserting Letters into their respective envelopes
Question
Answer
Case 3: Consider three letters L1, L2 & L3 and their corresponding
envelopes E1, E2 & E3.
In how many ways can the letter be put into a wrong envelope?
There are two way!
L1 E1
L2 E2
L3 E3
Example-
L1 can be put into E2 or E3
19-05-2021 16

17. Derangements- Notation and Formula
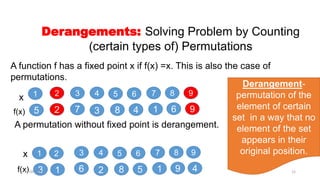
The number of derangement of n element set is called the nth
derangement number or recontres number, or the subfactorial of n and is
sometimes denoted !n or Dn:
And is given by the formula
𝐷𝑛 = 𝑛!
𝑖=0
𝑛
(−1)𝑖
𝑖!
Dn= n! [1-(1/1!)+ (1/2!)-(1/3!)…(1/n!)]
Simply:
19-05-2021 17

18. Illustrations on Derangements
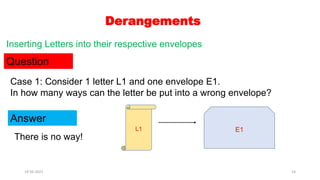
Question
In how many ways can you form a dancing couple from 3 boys and 3 girls
so that no boy dances with his respective girlfriend?
Answer
It is derangement of 3 boys and 3 girls.
Dn= n! [1-(1/1!)+ (1/2!)-(1/3!)…(1/n!)]
=3! [1-(1/1!)+ (1/2!)-(1/3!)]
=2 ways
19-05-2021 18

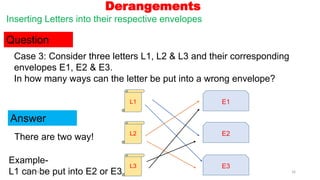
19. Illustration on Derangements
The arrangement of 6 people in 6 seats can be done in 6! ways. Now in
how many ways can you arrange them again such that none of them are
occupying their original position?
Question
Answer
Derangement value of 6
1 2 3 4 5 6 Dn= n! [1-(1/1!)+ (1/2!)-(1/3!)…(1/n!)]
=6! [1-(1/1!)+ (1/2!)-(1/3!)+(1/4!)-(1/5!)+ (1/6!)]
= 265 ways
D0 D1 D2 D3 D4 D5 D6 D7 D8 D9
1 0 1 2 9 44 265 1854 14833 133496
19-05-2021 19

20. Generating Functions
Number of faces of
die=6
1st face P0,
2nd faceP1
3rd faceP2
.4th faceP3
5th face P4
6th faceP5
f(x) = P0+P1x+P2x2+P3x3+….P5 x5
f(x) is the generating function for series P0, P1, P2….
For a sequence, a0, a1,a2,..an,
The corresponding generating function,
f(x) = a0+ a1x+a2x2+….anxn = 𝑖=0
∞
a𝑖𝑥𝑖
19-05-2021 20

21. What is Generating Functions?
Generating functions are used to represent sequences efficiently by
coding the terms of sequence as coefficients of power of a variable in a
formal power series.
Problems in sequence Problems in variables
Generating functions
Easy
Difficult
19-05-2021 21

22. Question
Find generating functions of following series:
(a) 1,1,1,1,1,1,0, 0, 0
Ans: 1+x+x2+x3+x4+x5
(b) 1,4,6,4,1,0,0, 0
Ans: 1+4x+6x2+4x3+x4 =(1+x)4
(c) nC0, nC1, nC2, …., nCn
Ans: nC0+nC1x+nC2x2+…+nCnxn =(1+x)n
(d) 1,1,1,1,….
Ans: 1+x+x2+x3+x4+…= 𝑖=0
∞
𝑥𝑖
Binomial
theorem
19-05-2021 22

23. Some important sequences
and their results
Let Gn = f (x) =1+x+x2+..+xn (1)
Multiplying with x
xGn= x+x2+x3+.... (2)
Subtract Eq. no (2) with (1)
Gn- xGn =1
Gn =
1
1−𝑥
1+x+x2+..+xn =
1
1−𝑥
19-05-2021 23

24. Scaling Rule
Multiplying a generating function by a constant scales every term in the
associated sequence by the same constant.
[f0,f1,f2,f3..]↔ F(x)
c[f0,f1,f2,f3..]↔ cF(x)
Example:
[1,0,1,0,1,0..] ↔1+x2+x4+...=
1
1−𝑥2
Note: To indicate correspondence between a sequence and its
generating function with a double sided-arrow.
19-05-2021 24
Multiplying with 2:
2+2x2+2x4+...=
2
1−𝑥2

25. Using Generating Functions to
Count things
From Binomial theorem,
The coefficient of xr in (1+x)n = nCr
The number of
ways of
choosing x from
r of the n factors
Question
Calculate the coefficient of xr in (1+x)3
3C0
3C1
3C2
3C3
1 3 3 1
(1+x)3= 1+3x+3x2+x3
19-05-2021 25

26. Question
To determine number of boxes containing n vegetables which we select
from potatoes, carrots, onions, tomatoes and broccoli such that the
following criterion are met.
Cases
The number of potatoes p in the box is either 0,
or 1
The no of carrots c in the box is an even number,
i.e., 0, 2, 4,6..
The no of onions o in the box is either 0,1 or 2
The no of tomatoes t in the box is an odd number,
i.e., 1, 3, 5,..
The no of broccoli bunches b is some multiple of
3, i.e., 0,3,6…
Elements in sequence Factor in generating
function
0, 1 (1+x)
0, 2,4,6
…
(1+x2+ x4+…)
0,1,2 (1+x+ x2)
1,3,5,.. (x+x3+ x5+…)
(1+x3+ x6+…)
00,3,6…
F(x) = (1+x) (1+x2+x4+..) (1+x+x2) (x+x3+ x5+…) (1+x3+ x6+…)
19-05-2021 26
Answer

27. 19-05-2021 27
1+x+x2+….xn =
1−𝑥𝑛+1
1−𝑥
Answer (Contd)
1+x2+x4+…..=
1
1−𝑥2 for /x/<1
x+x3+x5+….xn =
𝑥
1−𝑥2 for /x/<1 1+x3+x6=
1
1−𝑥3 for /x/<1
F(x) =
1−𝑥2
1−𝑥
.
1
1−𝑥2 .
𝑥
1−𝑥2 .
1−𝑥3
1−𝑥
.
1
1−𝑥3
F(x) =
𝑥 1−𝑥2 (1−𝑥3)
1−𝑥 2(1−𝑥2)2(1−𝑥3)
. =
𝑥
(1−𝑥)2 (1−𝑥2)
F(x) = 0 + 𝑥 + 2𝑥2 + 4𝑥3 + 6𝑥4 + 9𝑥5 + 12𝑥6 + 16𝑥7 + 20𝑥8 + 25𝑥9 + 30𝑥10 +
⋯ 𝐹 𝑥 ↔ (0,1,2,4,6,9,12,16,20,25,30 … )
(𝑎𝑖)𝑖=0
∞
= (0,1,2,4,6,9,12,16,20,25,30 … )

28. 19-05-2021 28
Let us try to verify at least one term:
Coefficient of x4 =6
There are 6 many 4-combinations that satisfy given criteria.
{p,c,c,t} {c,c,o,t} {p,t,t,t} {o,t,t,t} {t,b,b,b} {p,o,o,t}
Answer (Contd)
F(x) = 0 + 𝑥 + 2𝑥2
+ 4𝑥3
+ 6𝑥4
+ 9𝑥5
+ 12𝑥6
+ 16𝑥7
+ 20𝑥8
+ 25𝑥9
+ 30𝑥10
+
⋯