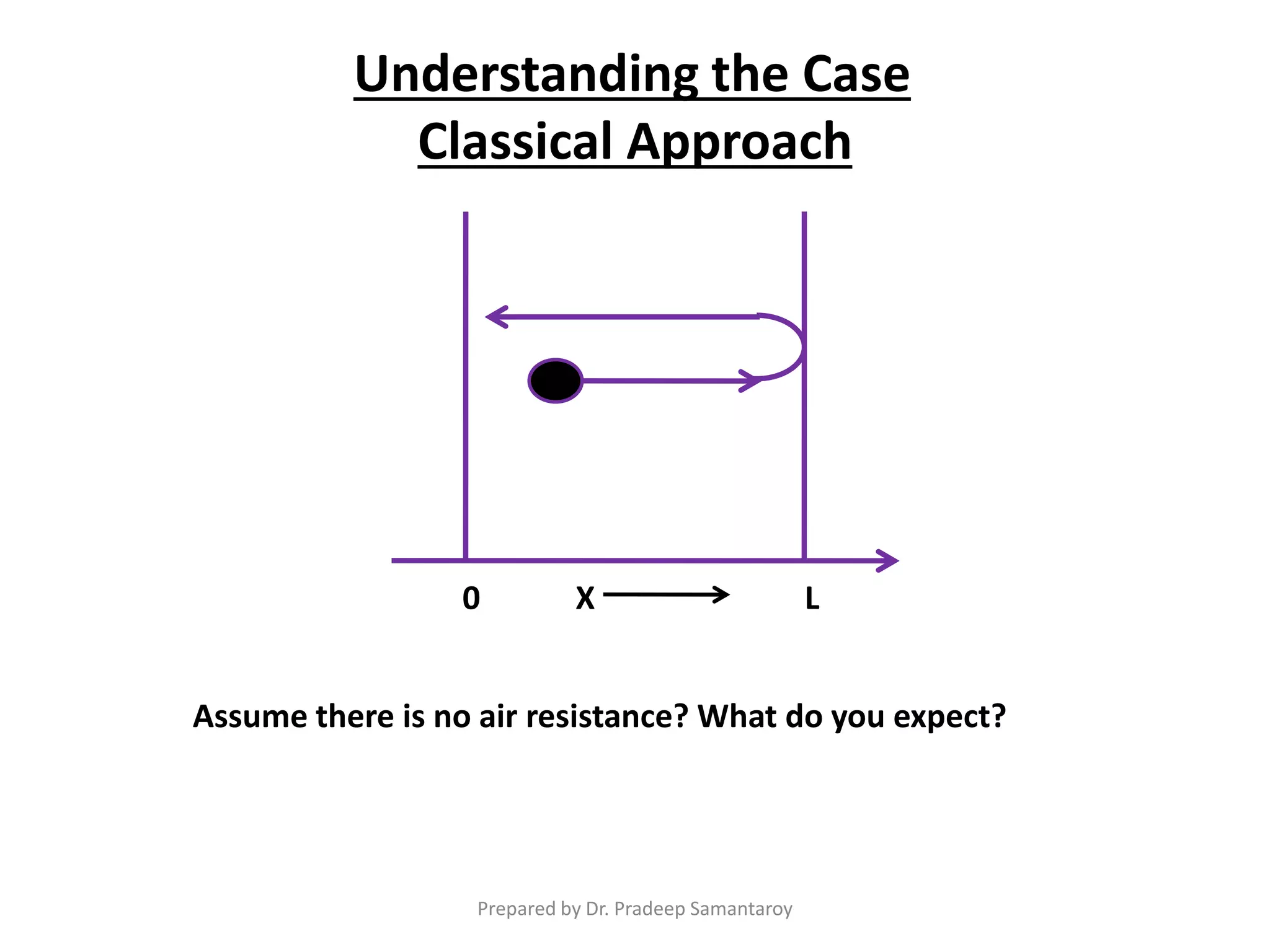
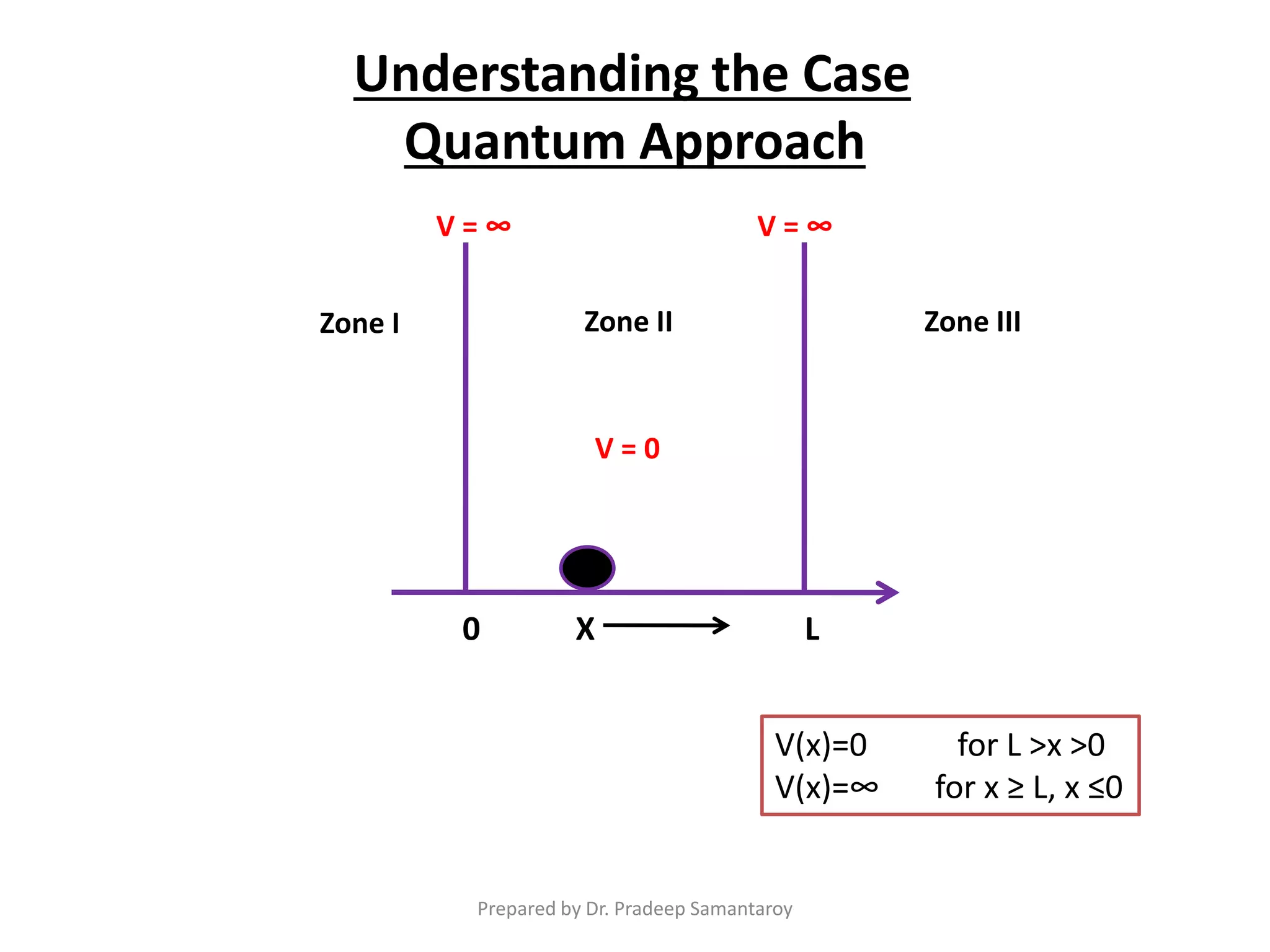
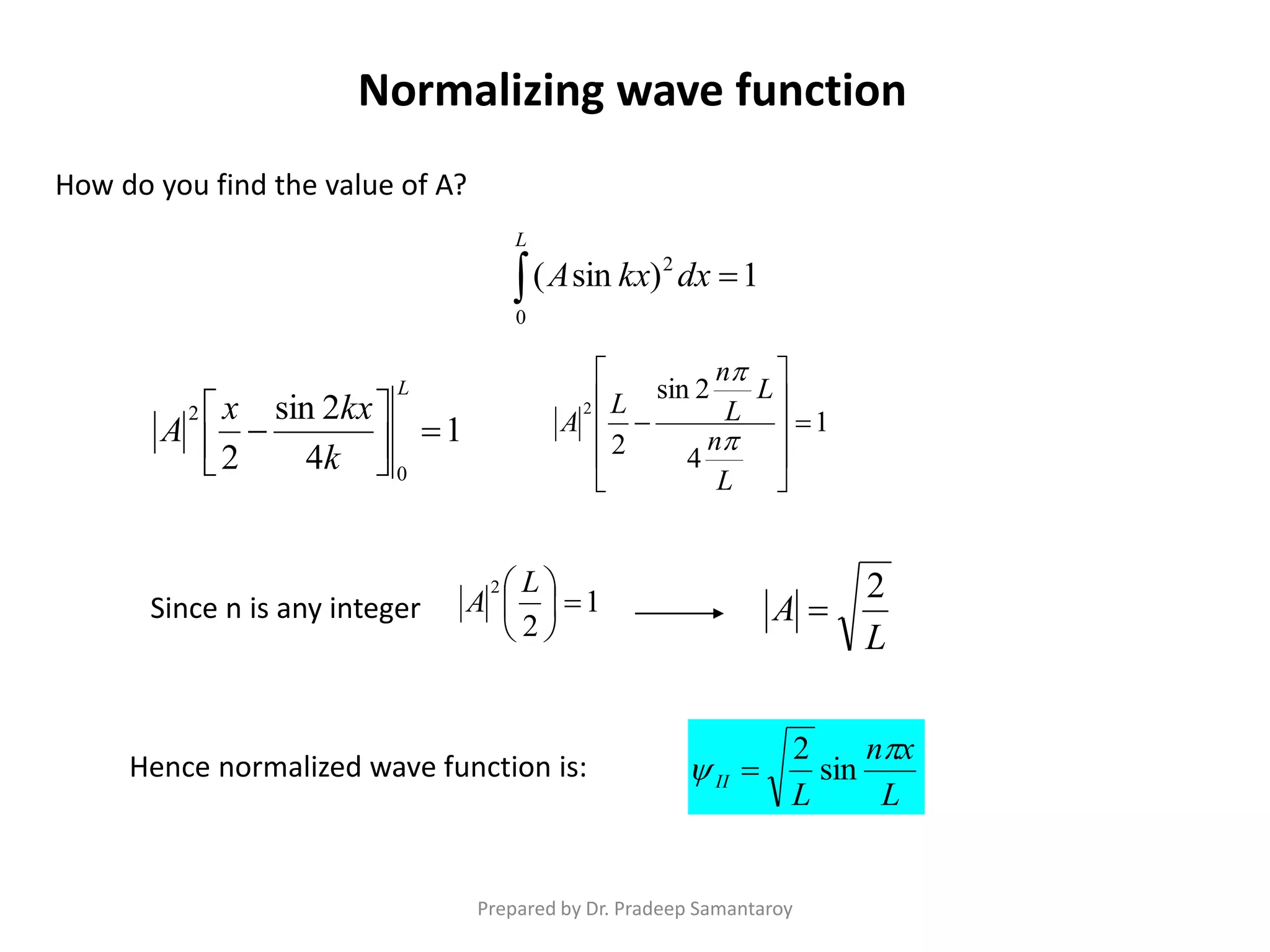
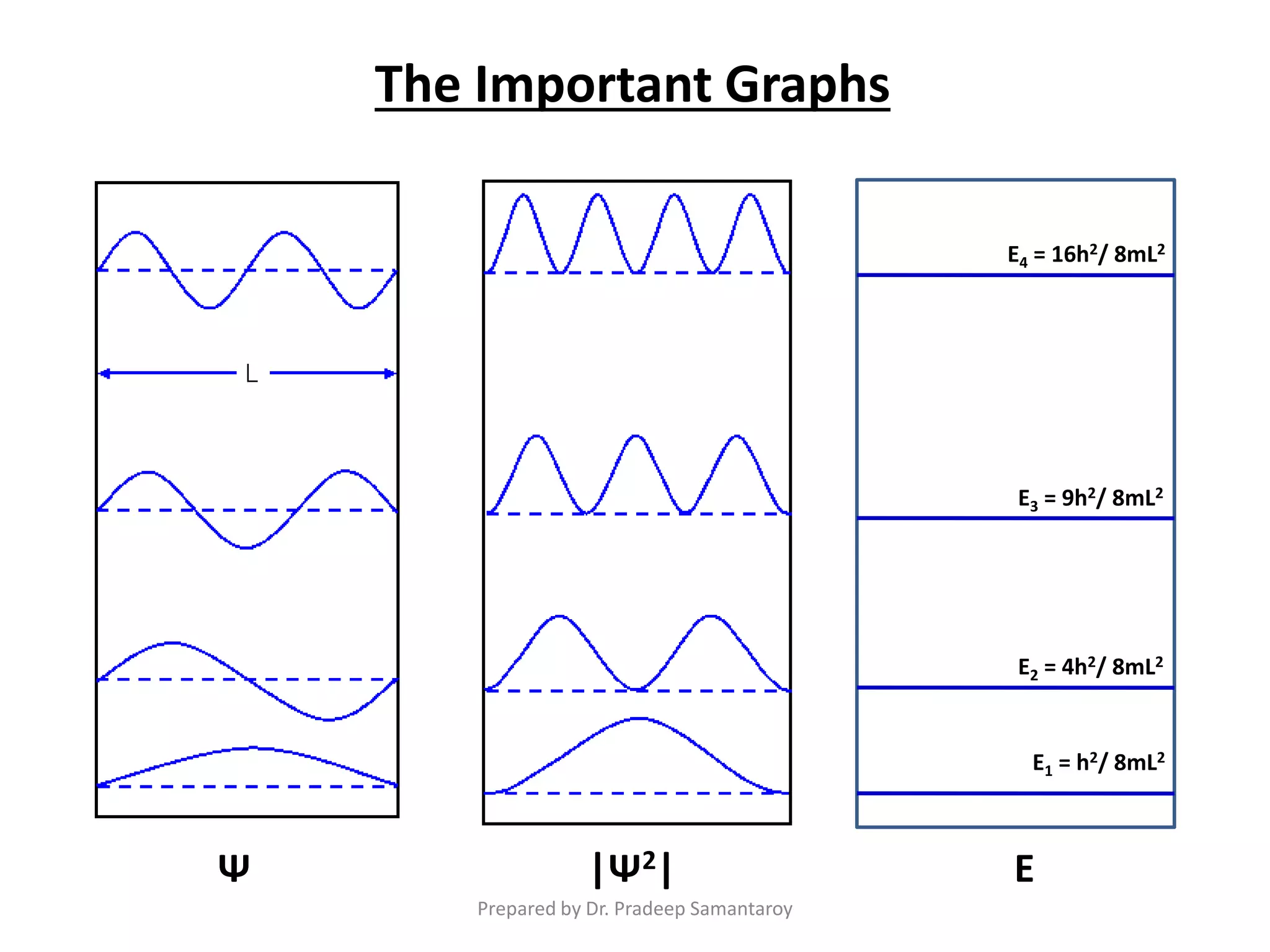
Dr. Pradeep Samantaroy discusses the classical and quantum approaches to understanding electron behavior in a one-dimensional box using Schrödinger's equation. He details wave function normalization, energy level calculations, and the implications of quantization. Numerical examples are provided to illustrate ground state energy and average energy values of confined particles.

1. Dr. Pradeep Samantaroy
Department of Chemistry
Rayagada Autonomous College, Rayagada
pksroy82@gmail.com; pksroy82@yahoo.in
9444078968

2. Understanding the Case
Classical Approach
0 X L
Assume there is no air resistance? What do you expect?
Prepared by Dr. Pradeep Samantaroy

3. Understanding the Case
Quantum Approach
0 X L
V = 0
V = ∞ V = ∞
Zone I Zone II Zone III
V(x)=0 for L >x >0
V(x)=∞ for x ≥ L, x ≤0
Prepared by Dr. Pradeep Samantaroy

4. Let’s solve the case…!


ExV
dx
xd
m


)(
)(
2 2
22

The Schrodinger’s equation for the electron in one dimensional box
can be represented as
Applying boundary conditions to Zone I


E
dx
xd
m


*
)(
2 2
22

0
2

Hence, the probability of finding electron in the Zone I is zero.
The same logic can be applied to zone III.
Prepared by Dr. Pradeep Samantaroy

5. 

E
dx
xd
m


2
22
)(
2


 2
2
2
)(
k
dx
xd



E
m
dx
xd
22
2
2)(


This is similar to the general differential equation:
kxBkxA cossin 
So we can start applying boundary conditions:
x=0 ψ=0 kBkA 0cos0sin0  0B
x=L ψ=0 0AkLAsin0  nkL 
where n is any integer
Solution to the Zone II
And the general solution to the differential equation is:
L
xn
AII

 sinNow the wave function becomes
Prepared by Dr. Pradeep Samantaroy

6. How do you find the value of A?
Normalizing wave function
1)sin(
0
2

L
dxkxA
1
4
2sin
2 0
2







L
k
kxx
A 1
4
2sin
2
2












L
n
L
L
n
L
A


Since n is any integer 1
2
2





 L
A
L
A
2

Hence normalized wave function is:
L
xn
L
II

 sin
2

Prepared by Dr. Pradeep Samantaroy

7. 2
2 2

mE
k 
m
k
E
2
22


2
22
42 m
hk
E 
2
2
2
22
42 

m
h
L
n
E 
2
22
8mL
hn
E 
Calculation of Energy Levels
Can n be zero??
Prepared by Dr. Pradeep Samantaroy

8. E1 = h2/ 8mL2
E2 = 4h2/ 8mL2
E3 = 9h2/ 8mL2
E4 = 16h2/ 8mL2
Ψ |Ψ2| E
The Important Graphs
Prepared by Dr. Pradeep Samantaroy

9. Let’s solve numericals
An electron is confined in a one-dimensional box of length 2 A°.
Calculate the ground state energy in electron volts.
Is quantization of energy level observable?
Prepared by Dr. Pradeep Samantaroy

10. Let’s solve numericals
Calculate the average value of the energy of a particle of mass m
confined to move in a one-dimensional box of width a and
infinite height with potential energy zero inside the box. The
normalized wave function of the particle is
Ψn(x) = (2/a)1/2 sin (nπx/a) where n = 1,2,3…
Prepared by Dr. Pradeep Samantaroy