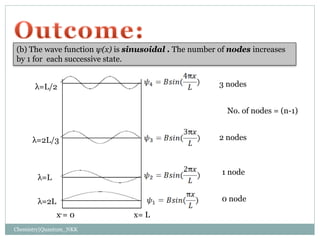
1. The particle is confined to a one-dimensional box of length L, with potential energy V=0 inside the box and V=infinity outside. 2. The wave functions and energy levels of the particle are quantized. The wave functions are sinusoidal with n nodes, and the energy is proportional to n^2. 3. The energy levels are spaced further apart at higher n values, with the spacing between levels increasing as the box size decreases.

1. The free moving particle
For free particle V(x)=0 implying that the 1D TISE is:
Now, let implying that
(1)
(2)
Compare with classical expression: =>
The de Broglie wavelength: or,
The 1D time independent Schrodinger Equation
is:
Chemistry|Quantum_NKK

2. Substitution of the above in eqn. (1)
gives,
(3)
Eqn. (3) is a standard second order differential eqn. with the general solutions:
Other form of the general solution is:
For free particle , no boundary conditions are available and hence any A and B
values are possible and therefore any E possible.
Chemistry|Quantum_NKK

3. 1. The particle can move freely inside the box (0 < x < L)
2. The potential energy of the electron inside the box is zero (V=0)
3. The potential energy at the edges is infinite, confining the electron to the box (V= α)
What we are looking for :
wave functions
energy of the particle
Particle in a One dimensional Box (PIB) model
m
x=0 x=L
V=α V=αV=0
V(x)
The wave function: ψ(x)
The energy: E
V(x)=α ; x<0, x>L
V(x)=0 ; x>0, x<L x
Chemistry|Quantum_NKK

4. For 1D PIB: The Schrodinger Equation:
With the general solutions:
Where, and
Now, there are boundary conditions:
Continuity of ψ(x) => ψ(0) =ψ(L) = 0
(i)
Chemistry|Quantum_NKK

5. (ii)
We can’t set B=0 which will imply that the particle can’t be found anywhere.
Therefore,
=>kL= nπ or k=(n π/L) n=1,2,3,…
It implies that k is not continuous but takes discrete values. So,
n=1,2,3,…
Energy , =>
The energy of stationary
or time independent sate
Chemistry|Quantum_NKK

6. THE ENERGY IS QUANTIZED
THE STATES ARE LABELLED BY QUANTUM NUMBER ‘n’ WHICH IS
AN INTEGER
(a) Energy spacing: Two successive energy states are separated by an energy gap:
Chemistry|Quantum_NKK

7. E3=9E1
E4=16E1
E5=25E1
The energy spacing between successive states
Spacing between successive states becomes progressively larger as ‘n’
increases
Chemistry|Quantum_NKK

8. (b) The wave function ψ(x) is sinusoidal . The number of nodes increases
by 1 for each successive state.
λ=2L
λ=L
λ=2L/3
λ=L/2
No. of nodes = (n-1)
0 node
1 node
2 nodes
3 nodes
x = 0 x= L
Chemistry|Quantum_NKK

9. (c) The energy spacing increases as the box size decreases.
Application of this model up to a good approximation is pi-bonding electrons
in aromatics. Electronic transitions shifts to lower energies as the molecule
size increases.
Chemistry|Quantum_NKK

10. Born interpretation:
Probability of finding the particle in the interval between x to x+dx
= probability of finding the particle in interval
The total probability of finding the particle somewhere within the
box must be 1.
Normalization Condition
Therefore, for PIB model:
Chemistry|Quantum_NKK

11. The integral we need to calculate is:
or,
We used the standard integral:
Therefore the normalized wave function is:
n=1,2,3,…
Normalization constant
Chemistry|Quantum_NKK

12. Expectation values or Average values
For 1 D PIB:
or,
Standard integral used: In our case,
It means the average particle position is in the middle of the box. This is
exactly what we would expect, because the particle is equally likely to be in
each half of the 1D box.
Chemistry|Quantum_NKK

13. Test your knowledge:
Is this state an eigen function of the position operator?
Problem: Assume that a particle is confined to a box of length
L, and the system wave function is
Chemistry|Quantum_NKK
Ref: 1. Physical Chemistry by Atkins and Paula
2. Molecular Quantum Mechanics by Friedman and Atkins