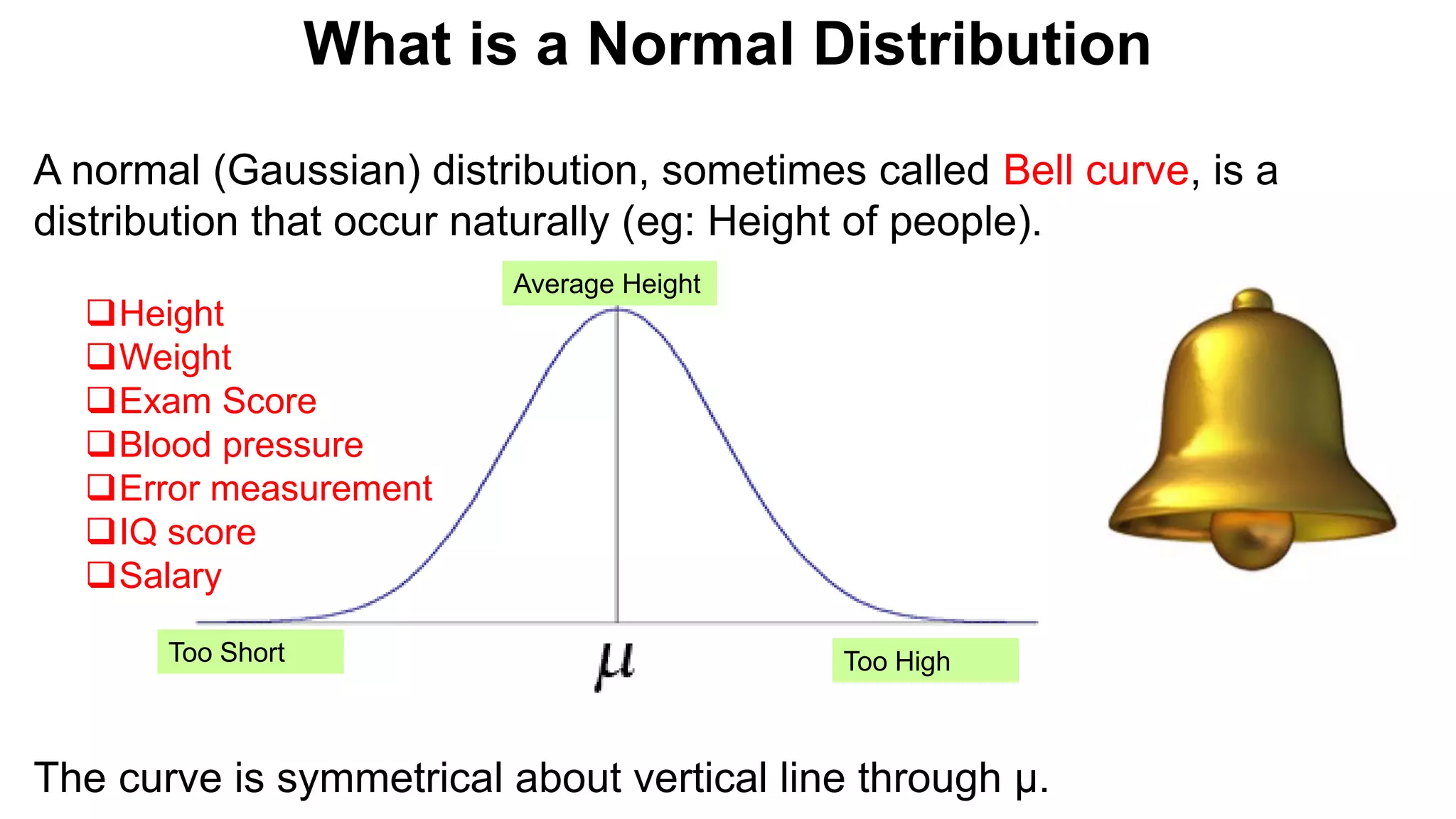
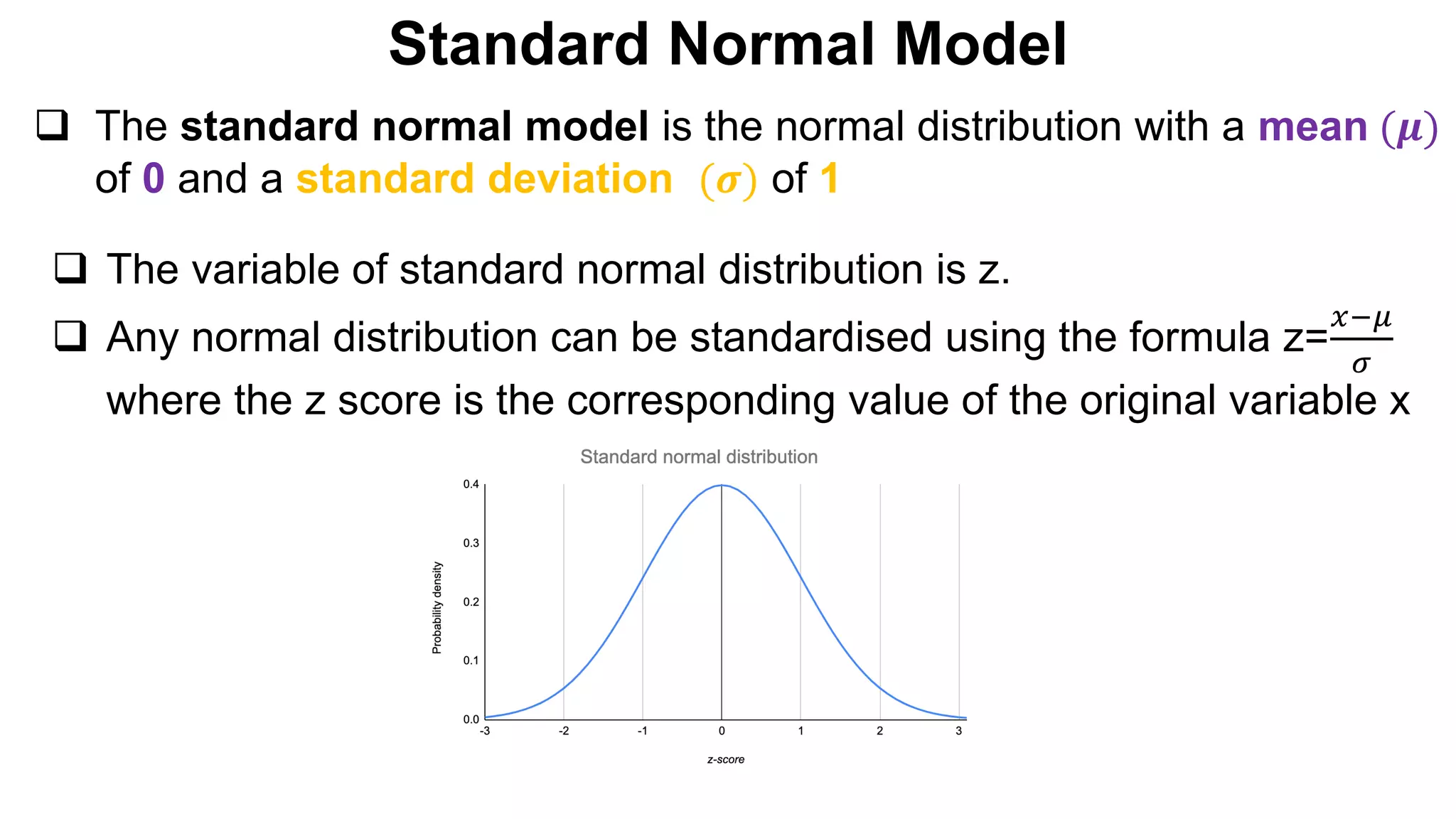
The document discusses normal distribution, also known as the Gaussian or bell curve, which is symmetrical and commonly appears in natural phenomena like height. It defines the normal density function, properties such as equality of mean, mode, and median, and explains the standard normal model which has a mean of 0 and standard deviation of 1. Additionally, it provides examples of applying normal distribution in calculating probabilities related to income and exam scores.

1. Normal Distribution
Dr. Anjali Devi J S
Guest Faculty
School of Chemical Sciences
M G University

2. What is a Normal Distribution
A normal (Gaussian) distribution, sometimes called Bell curve, is a
distribution that occur naturally (eg: Height of people).
The curve is symmetrical about vertical line through µ.
Too Short Too High
Average Height
Height
Weight
Exam Score
Blood pressure
Error measurement
IQ score
Salary

3. Normal Distribution Function
The function defined by
𝑛 𝑥 =
1
2𝜋
𝑒−
1
2𝑥2
is called normal density function.
Its integral
𝑁 𝑥 =
1
2𝜋 −∞
+∞
𝑒−
1
2
𝑦2
𝑑𝑦
is the normal distribution function.

4. Notation
If a random variable X is normally distributed (i.e., its probability function
uses a normal distribution), then we write:
𝑋~𝑁(𝜇, 𝜎2)
The random variable X
Is distributed
Using a Normal distribution with mean µ
and variance 𝜎2
Example Suppose X is a normal random variable with 𝜇=32 and 𝜎2=6,
then notation:
𝑋~𝑁(32,6)

5. Properties
 The mean, mode, and median are all equal.
 The curve is symmetric at the centre (i.e., around the mean µ).
 Exactly half of the values are to the left of center and exactly half the
values are to the right.
 The total area under the curve is 1.
−∞
+∞
𝑁 𝑥 𝑑𝑥 = 1

6. Standard Normal Model
 The standard normal model is the normal distribution with a mean (𝝁)
of 0 and a standard deviation (𝝈) of 1
 The variable of standard normal distribution is z.
 Any normal distribution can be standardised using the formula z=
𝑥−𝜇
𝜎
where the z score is the corresponding value of the original variable x

7. Standard Normal Model
Distance from mean in
terms of standard
deviation in one direction
0-1 1-2 2-3 Over 3
Proportion of area in the
above range
34% 14% 2% Negligible

8. Question
Daily income of worker follows normal distribution with mean Rs 1000
and standard deviation Rs 100/-. Find the probability of the income
less than Rs 1100/-
z=
𝑥−𝜇
𝜎 x=1100 𝜇 =1000 𝜎 =100
z=1
P (x<1000)=𝑃(𝑧 < 1)
z =0 z =1
𝑃 𝑧 < 1 = 𝑃 𝑧 < 0 + 𝑃(𝑧 = 1)
𝑃 𝑧 < 1 = 0.50 + 𝑃(𝑧 = 1)
= 0.50 + 0.34
= 0.84

9. Question
The bottom 30% of students failed an end semester exam. The mean
of the test was 120 and the standard deviation was 17. What was the
passing score?
µ =120
x
z=
𝑥−𝜇
𝜎
x= z𝜎 + 𝜇
=0.52
Fail 30% Pass 70%
x= z𝜎 + 𝜇
z= 0.52
x= 111.16