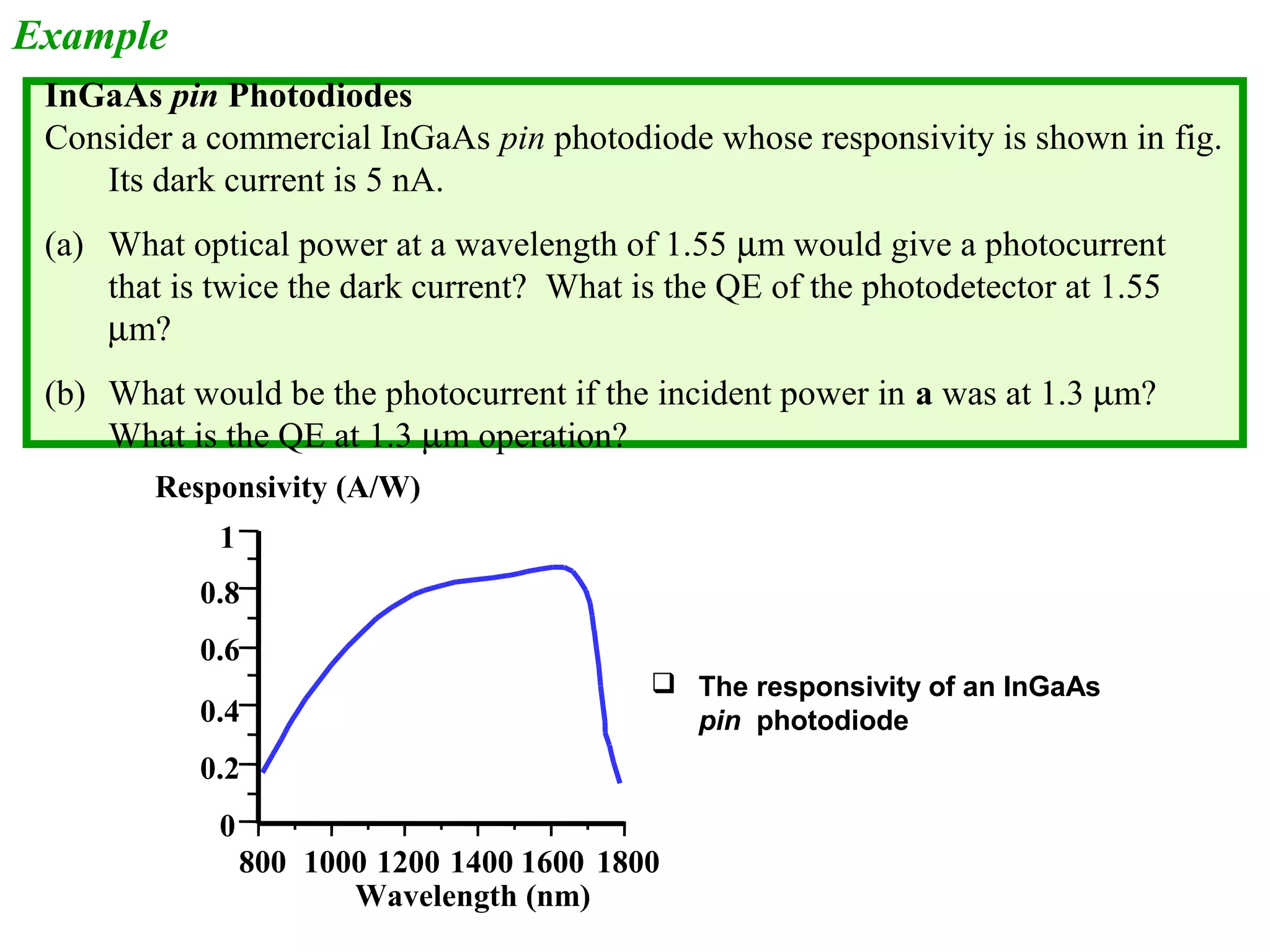
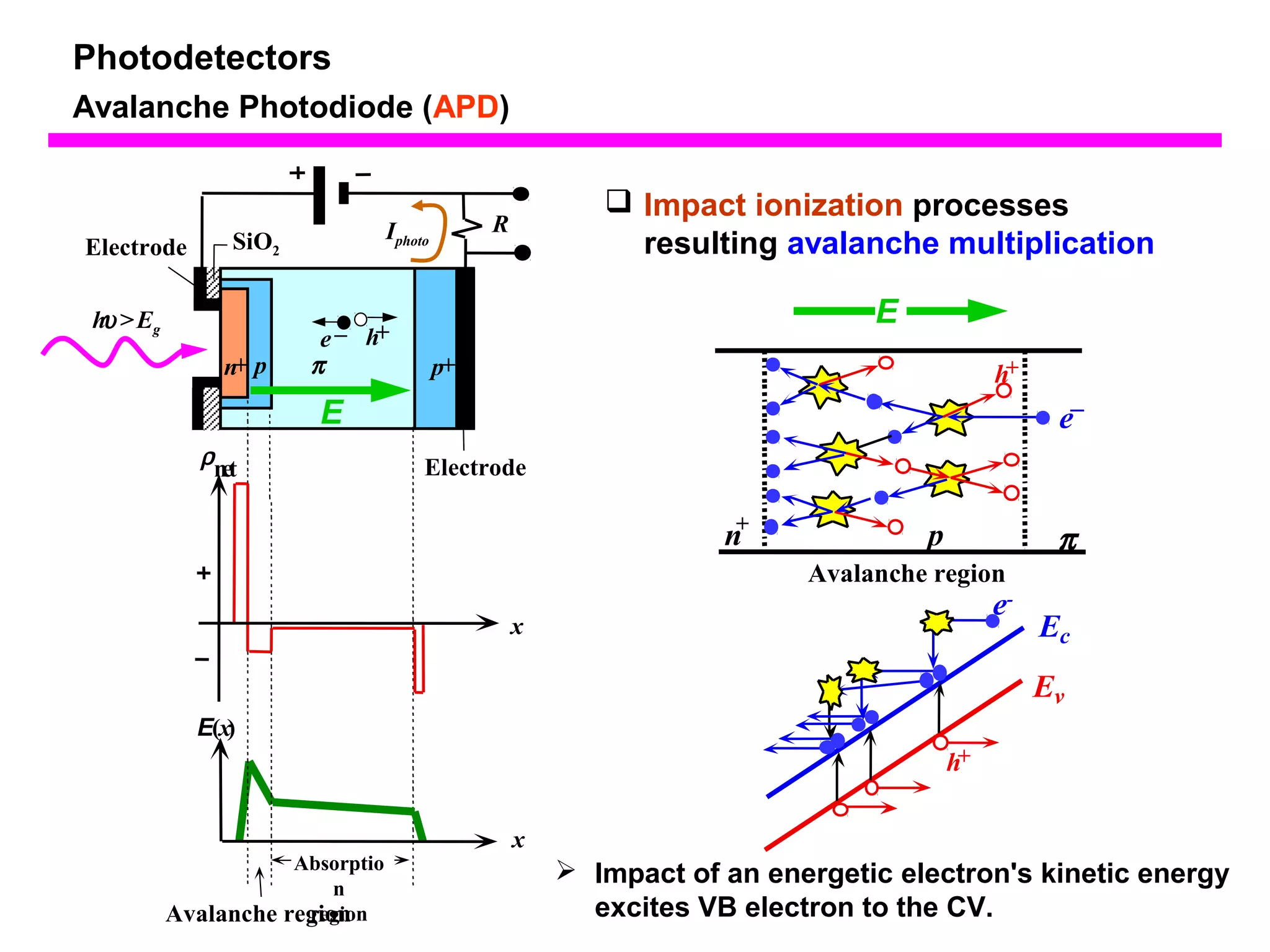
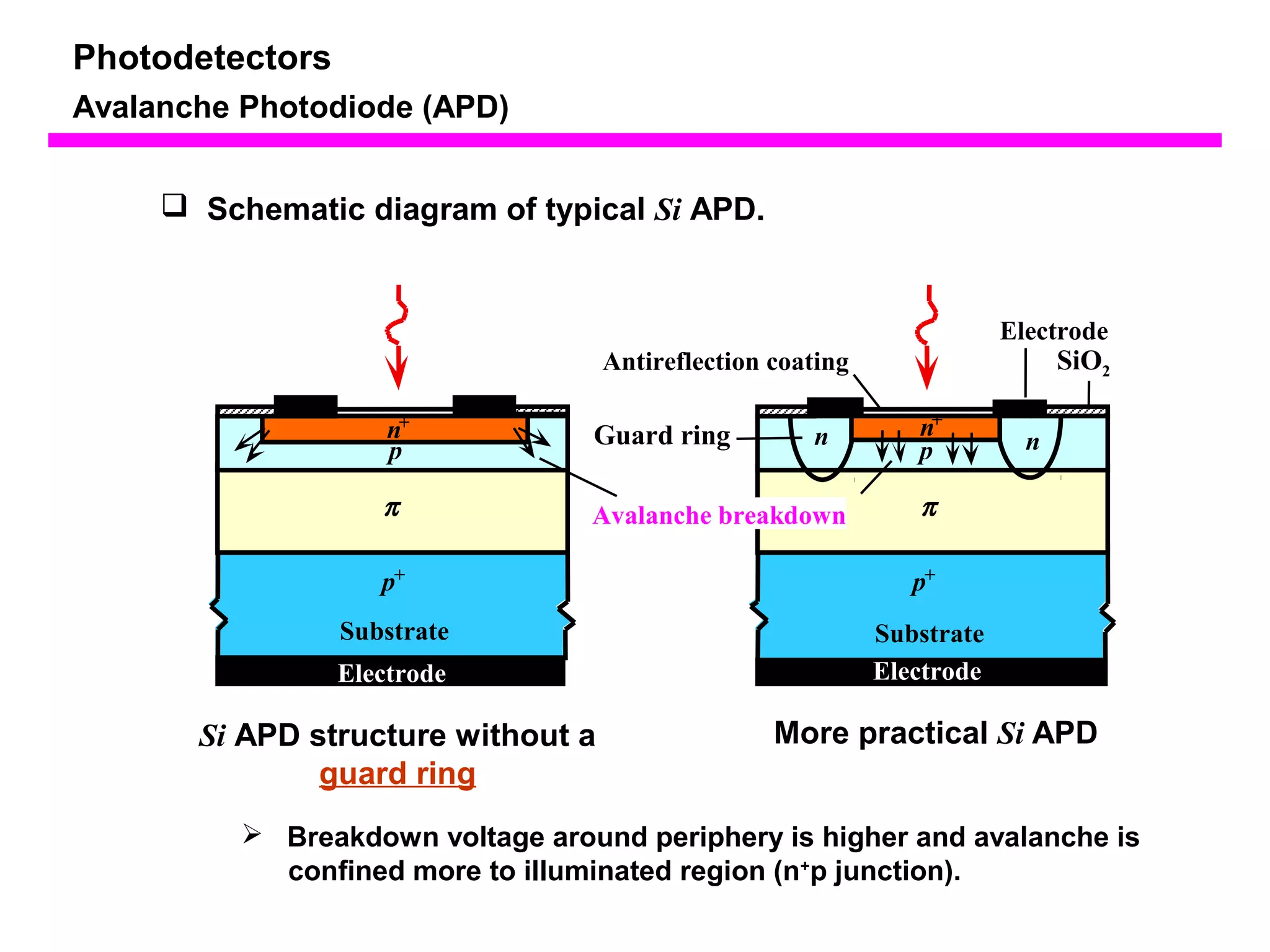
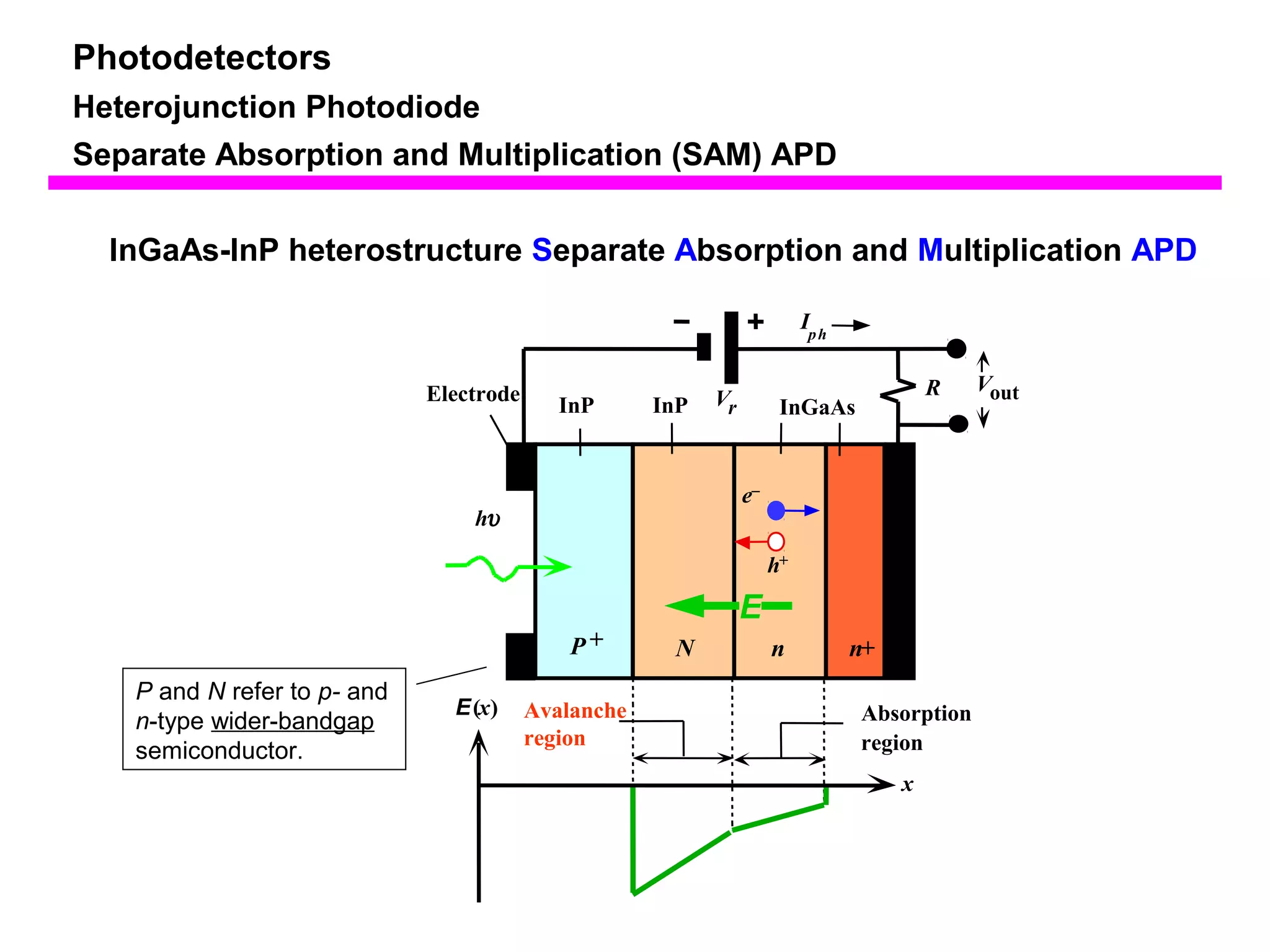
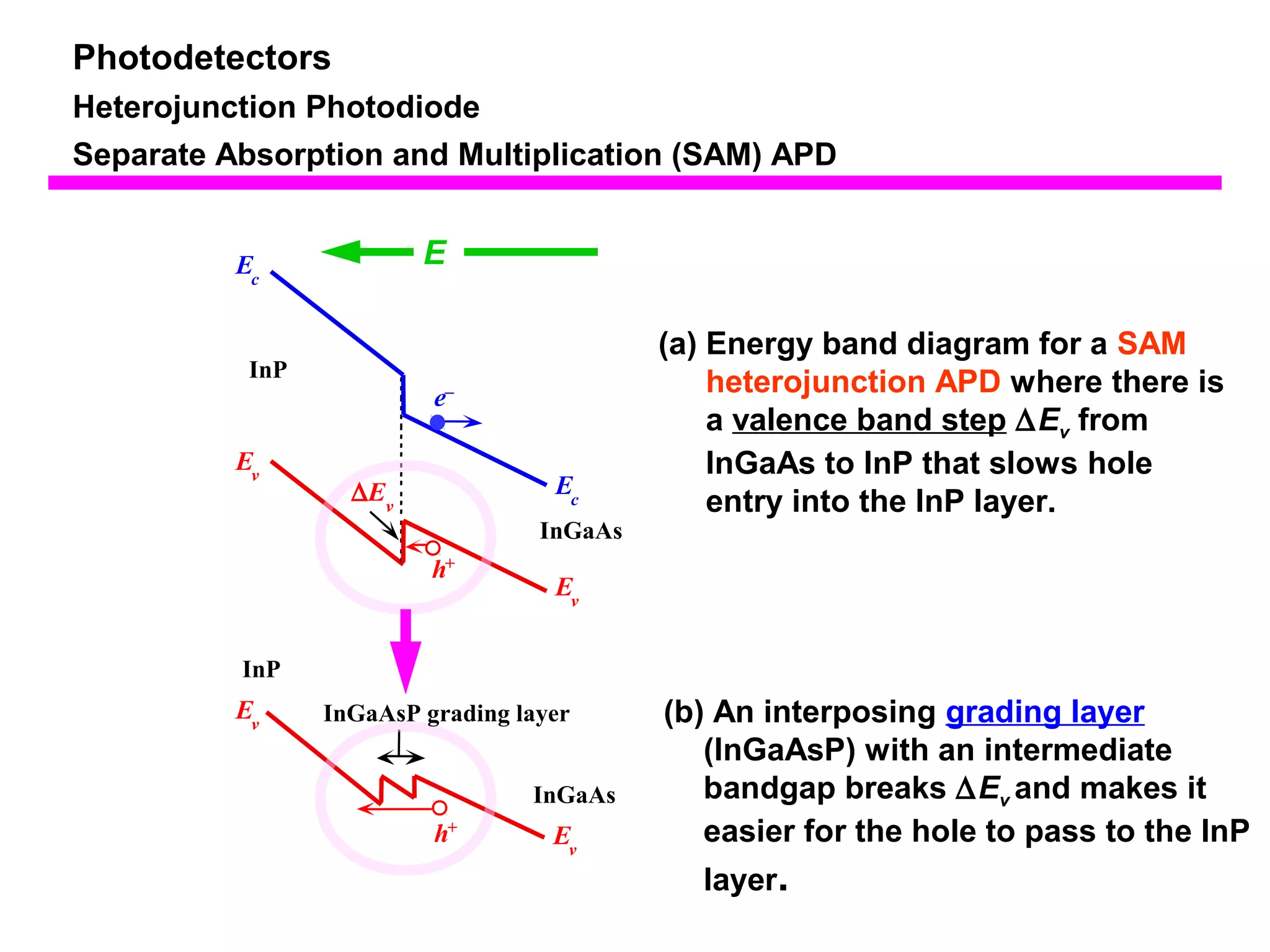
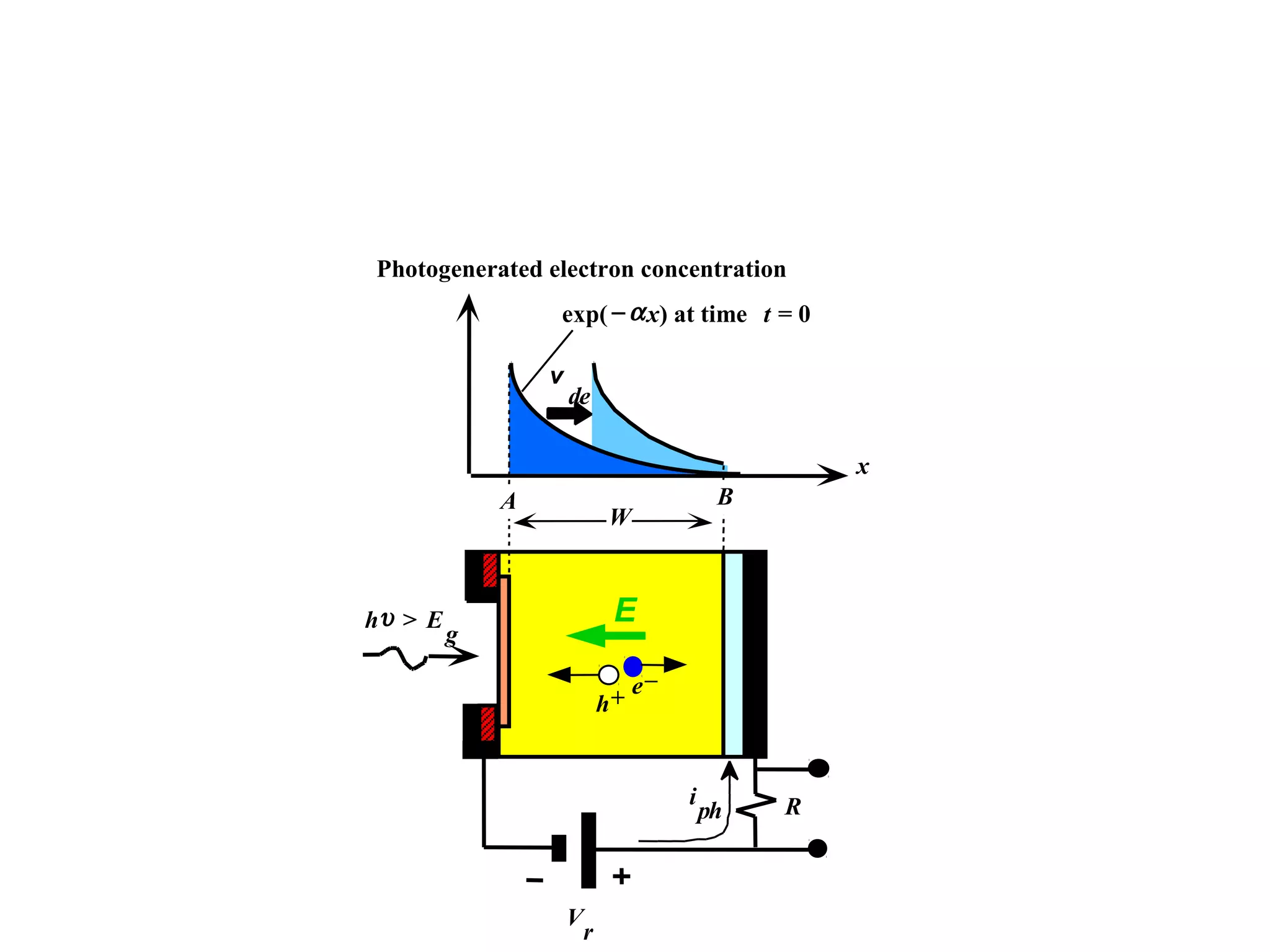
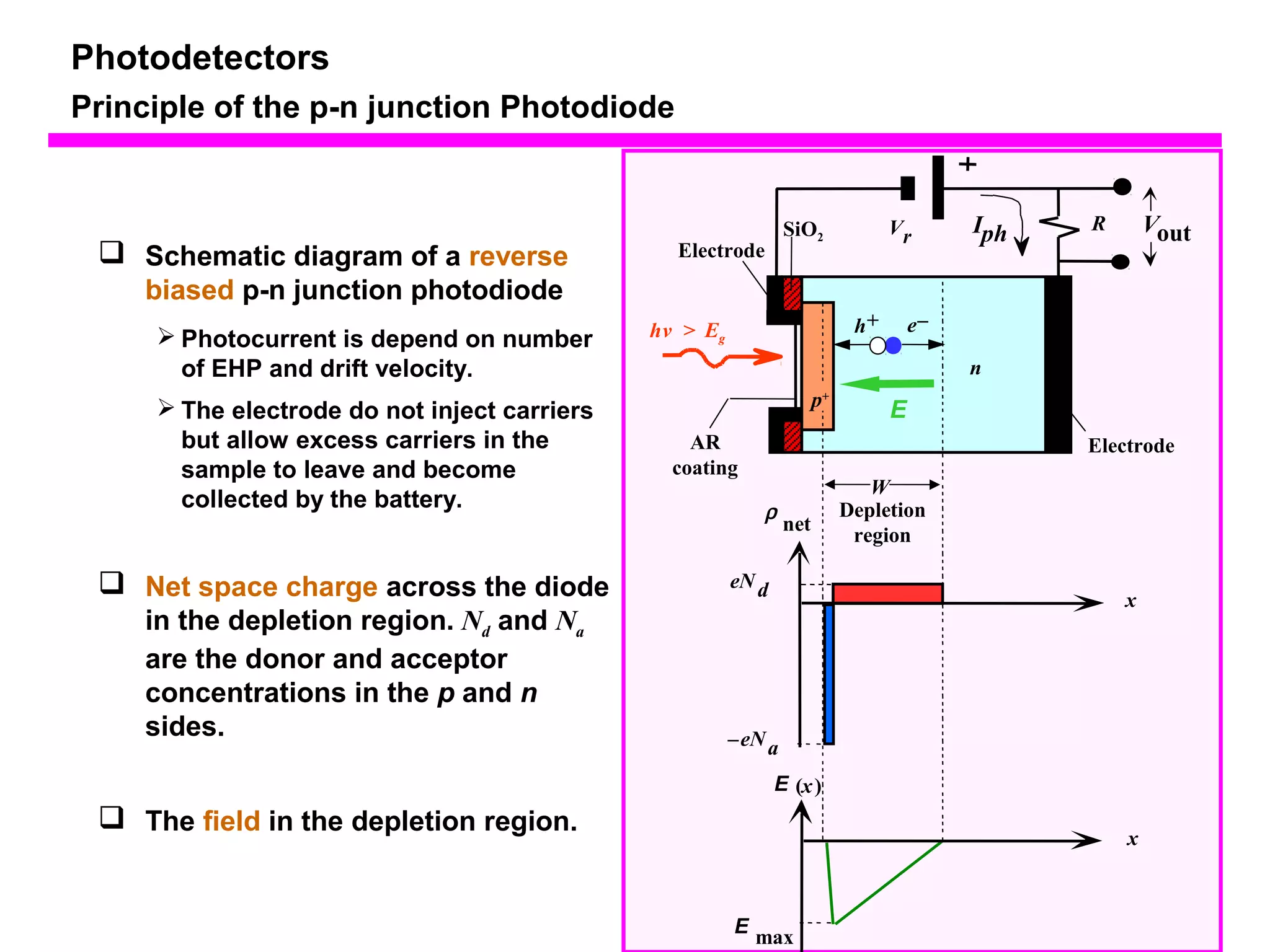
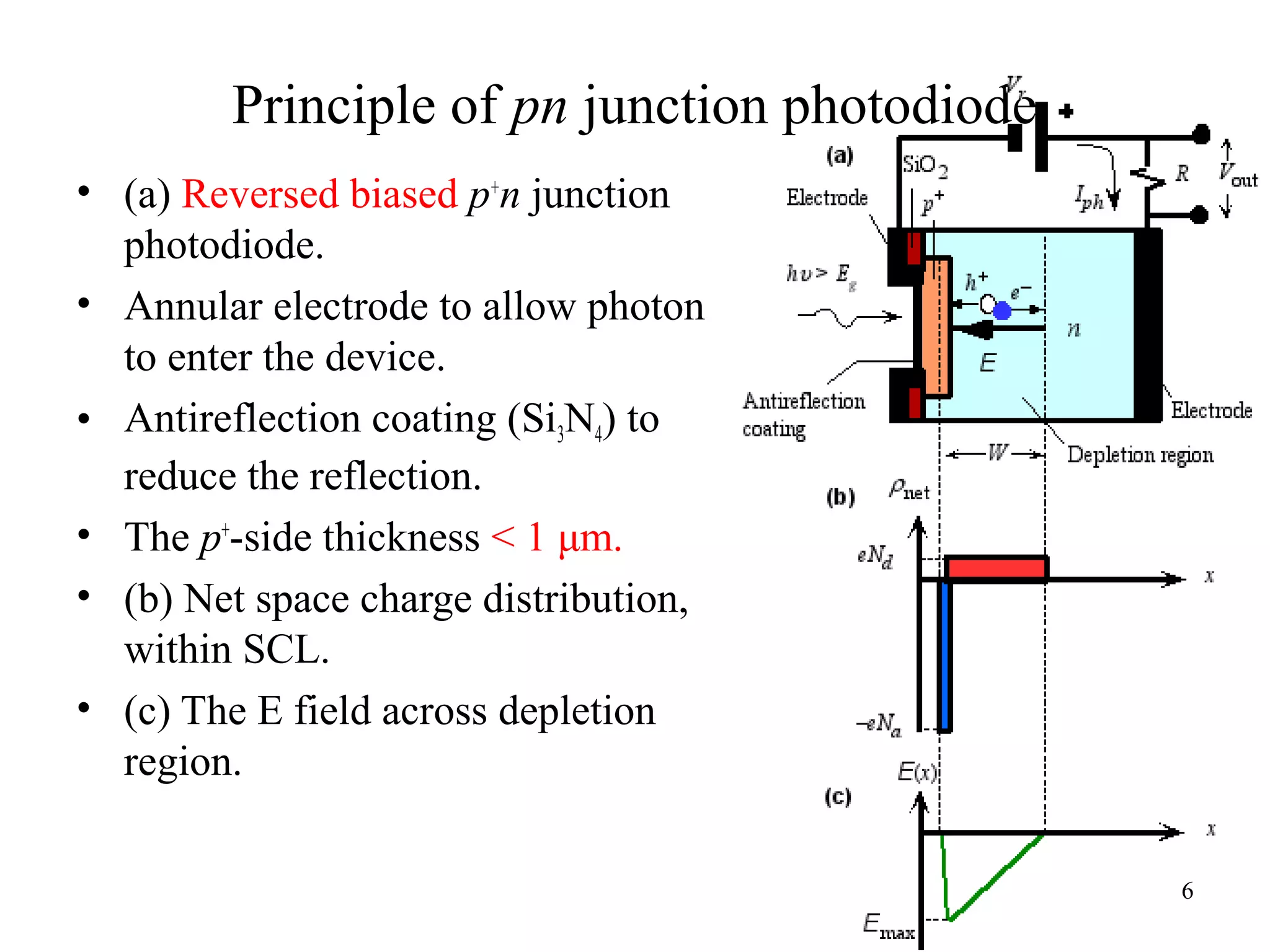
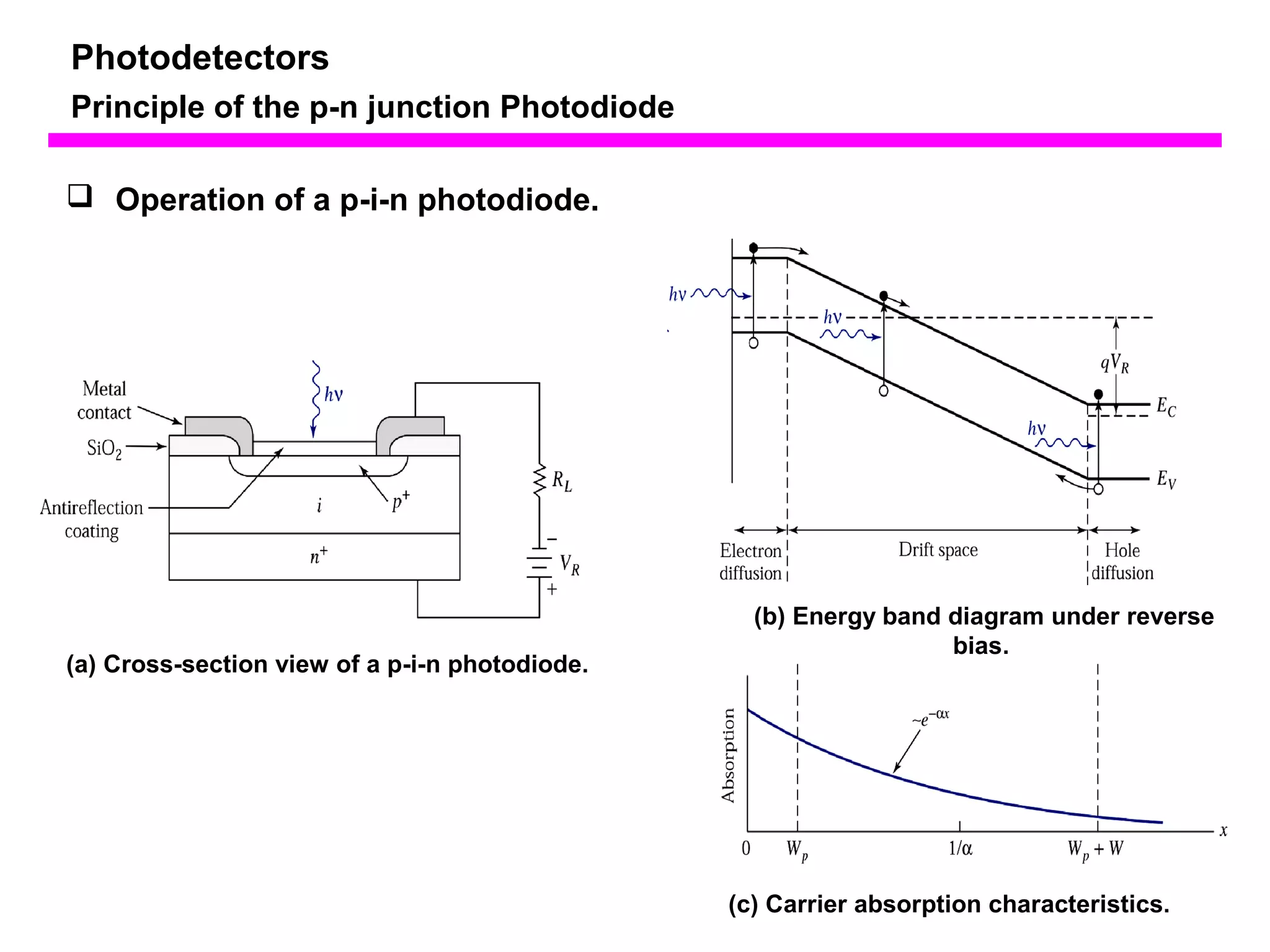
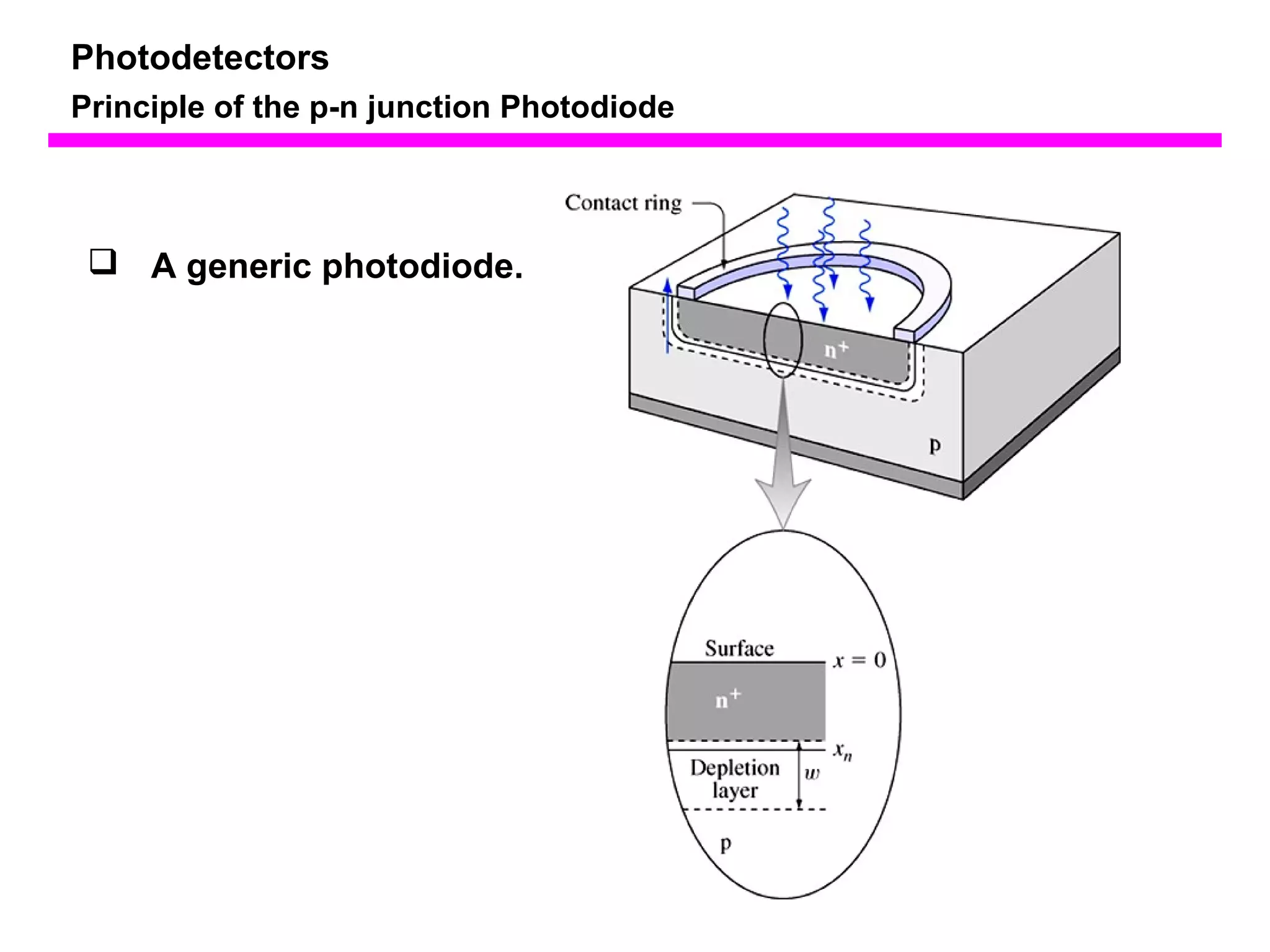
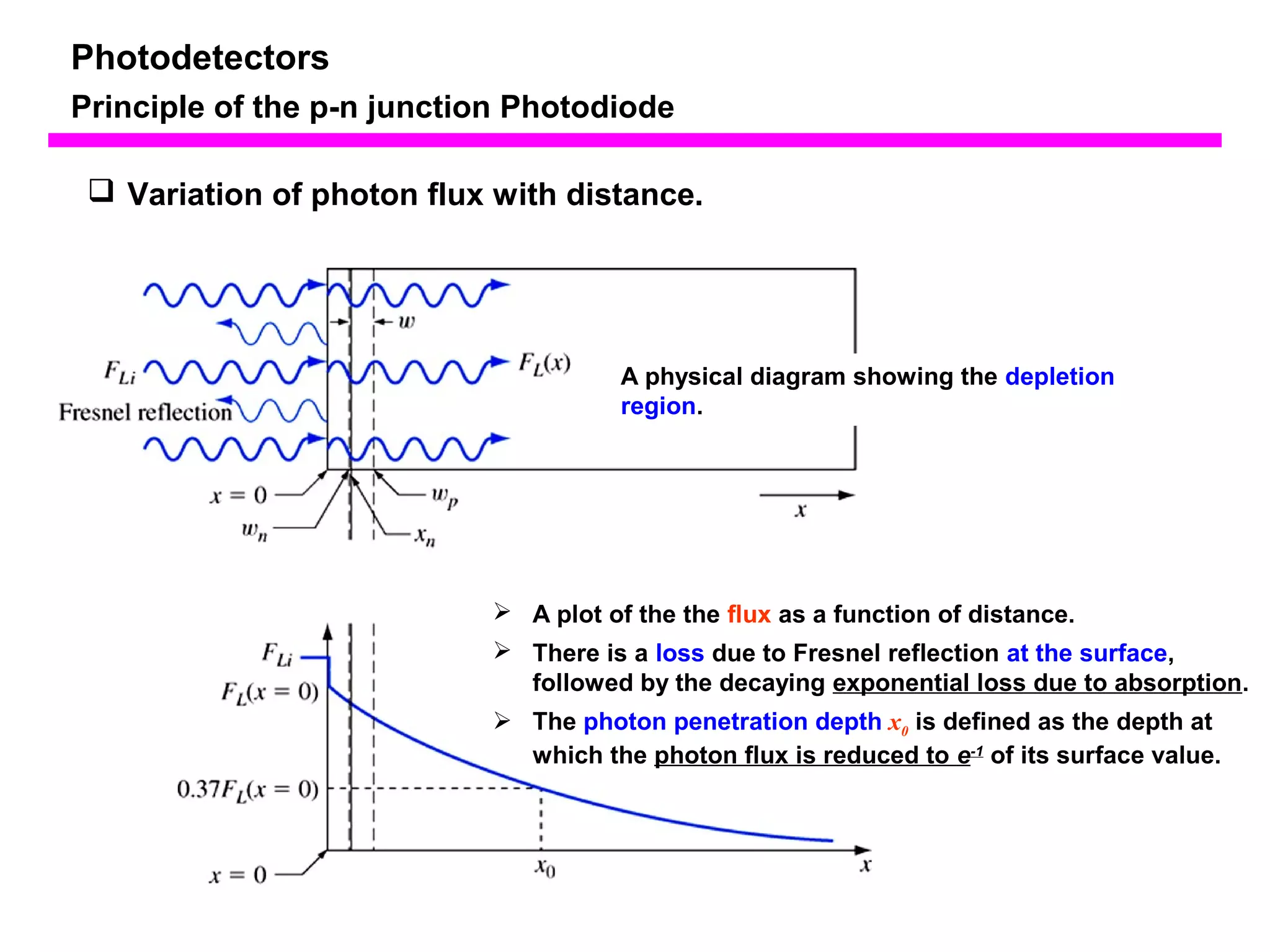
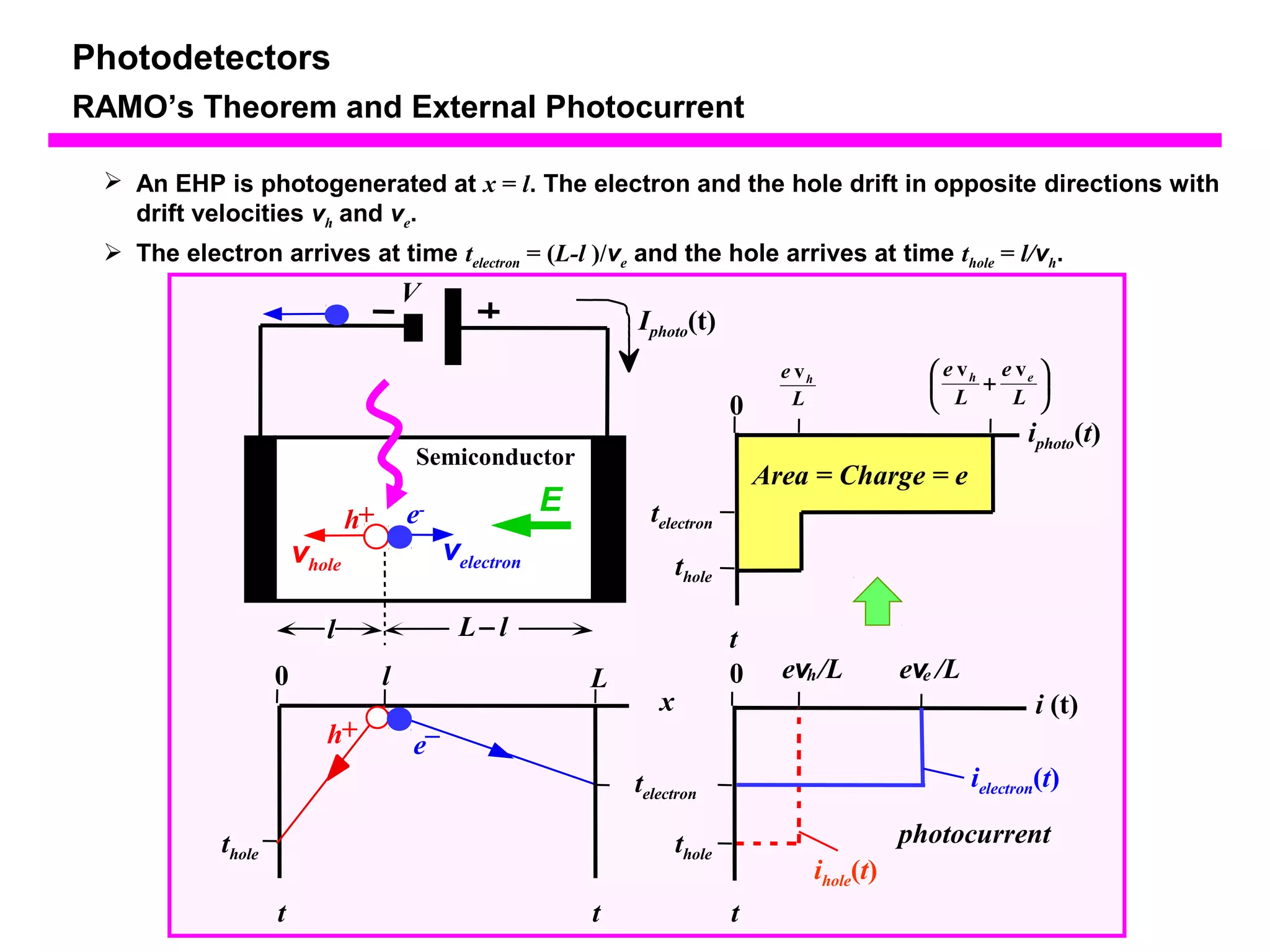
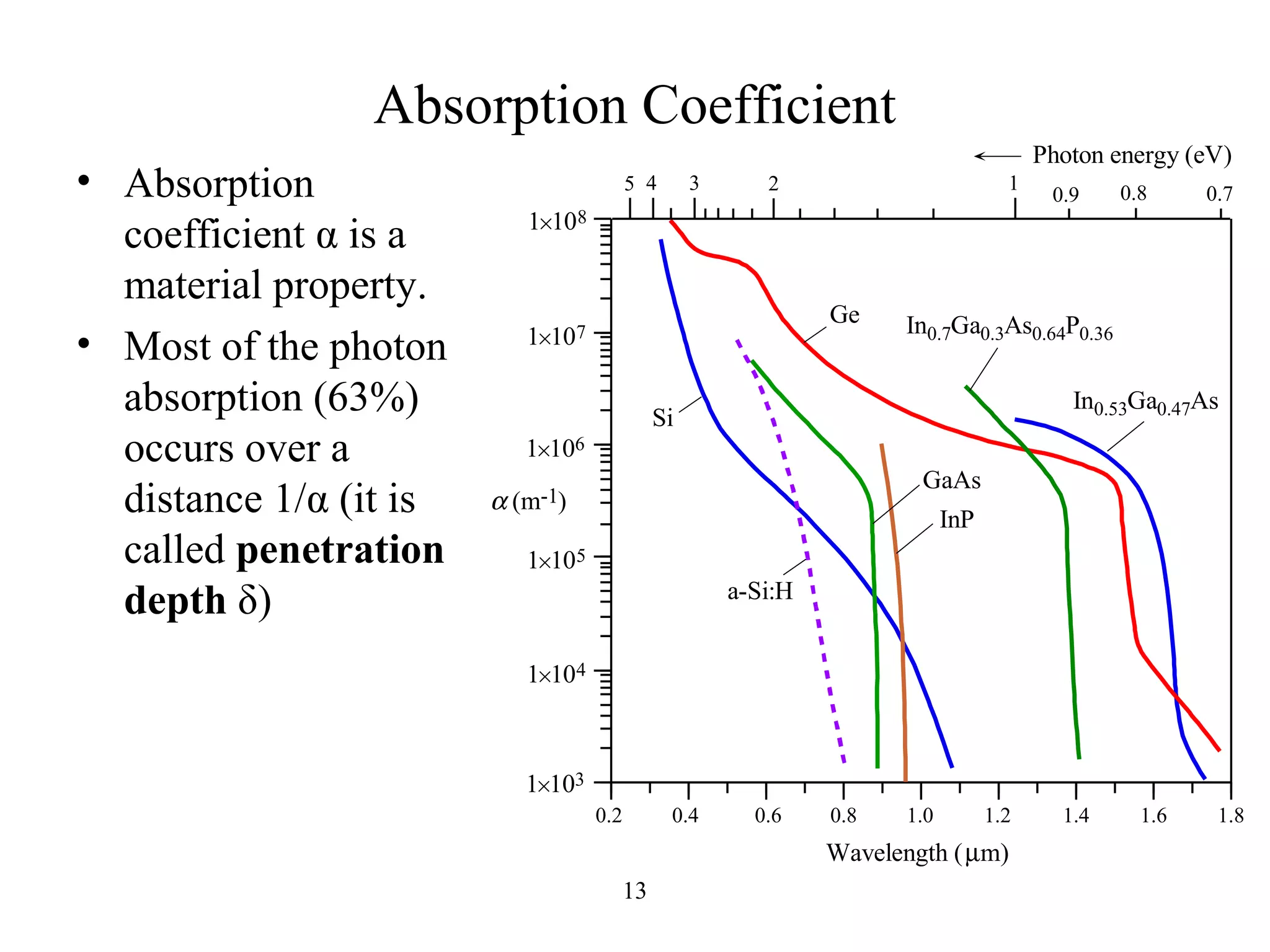
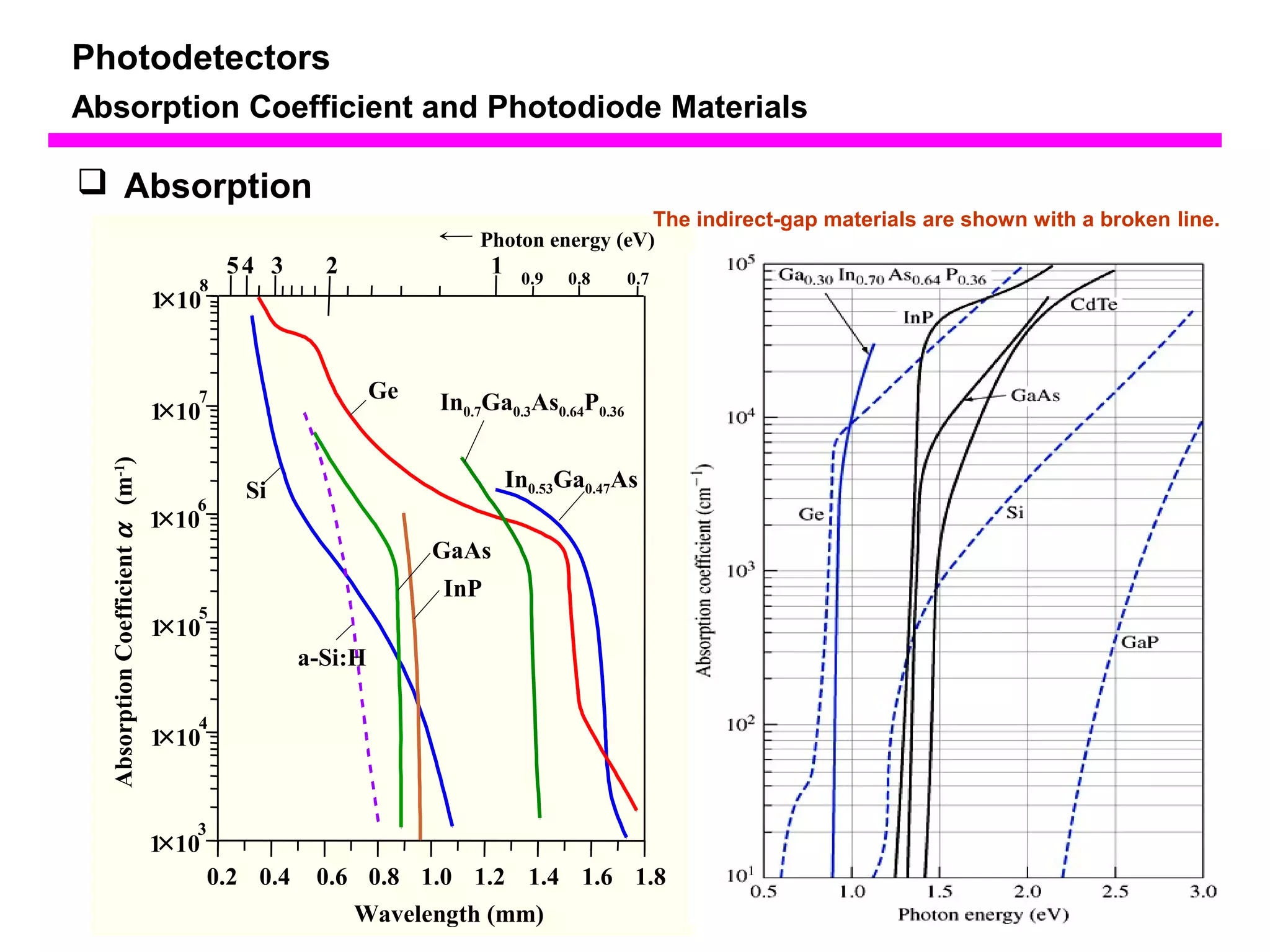
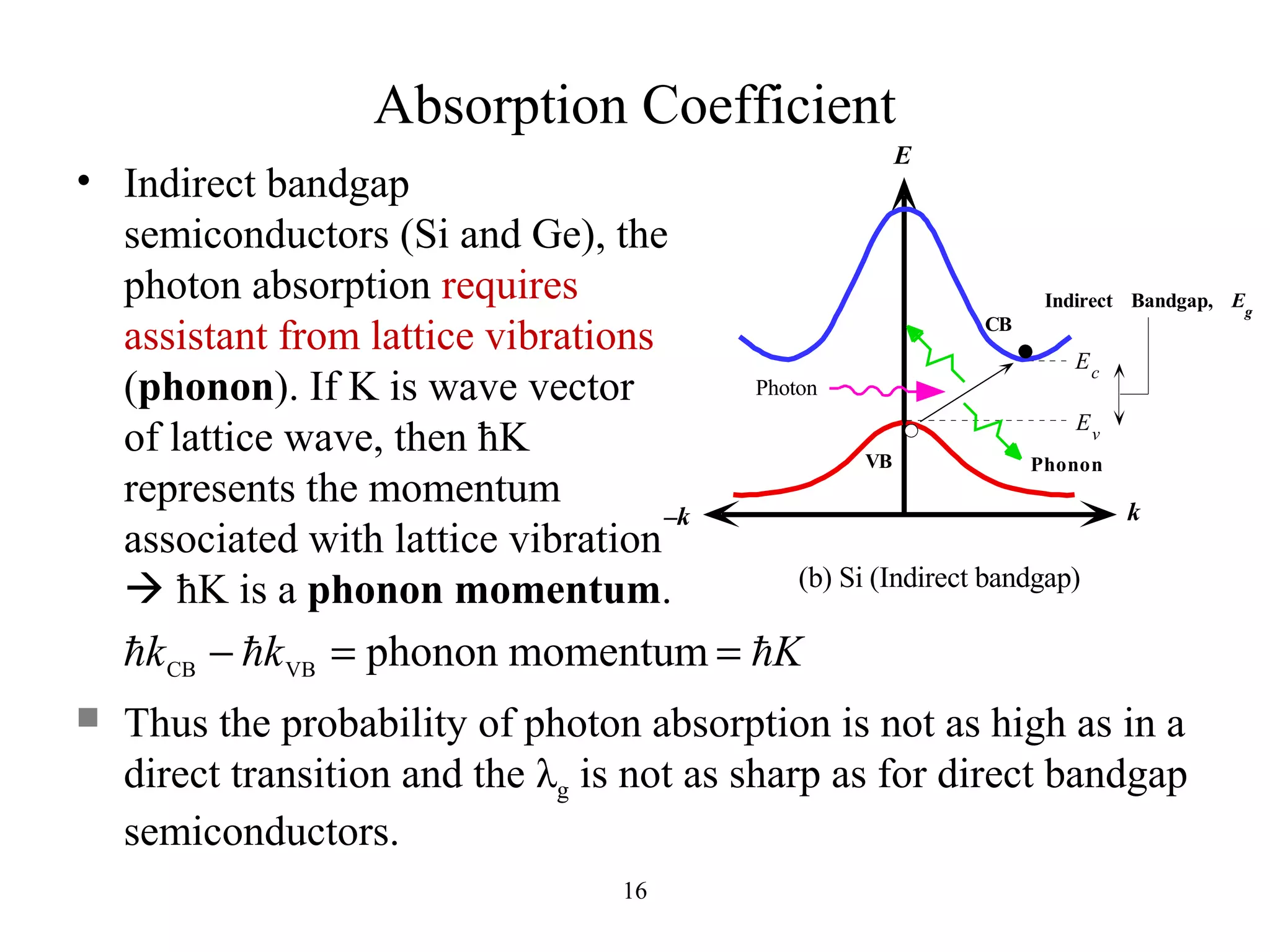
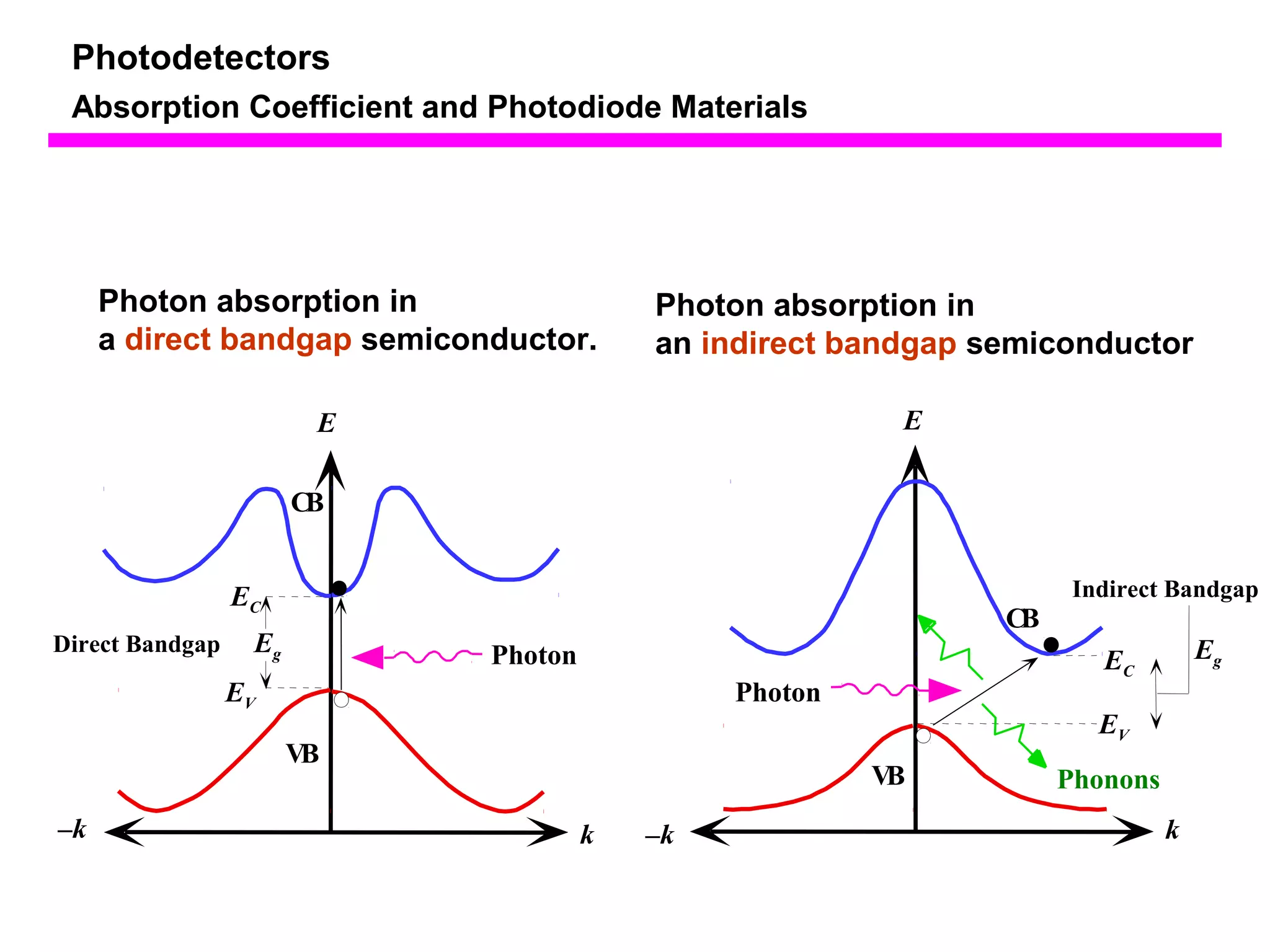
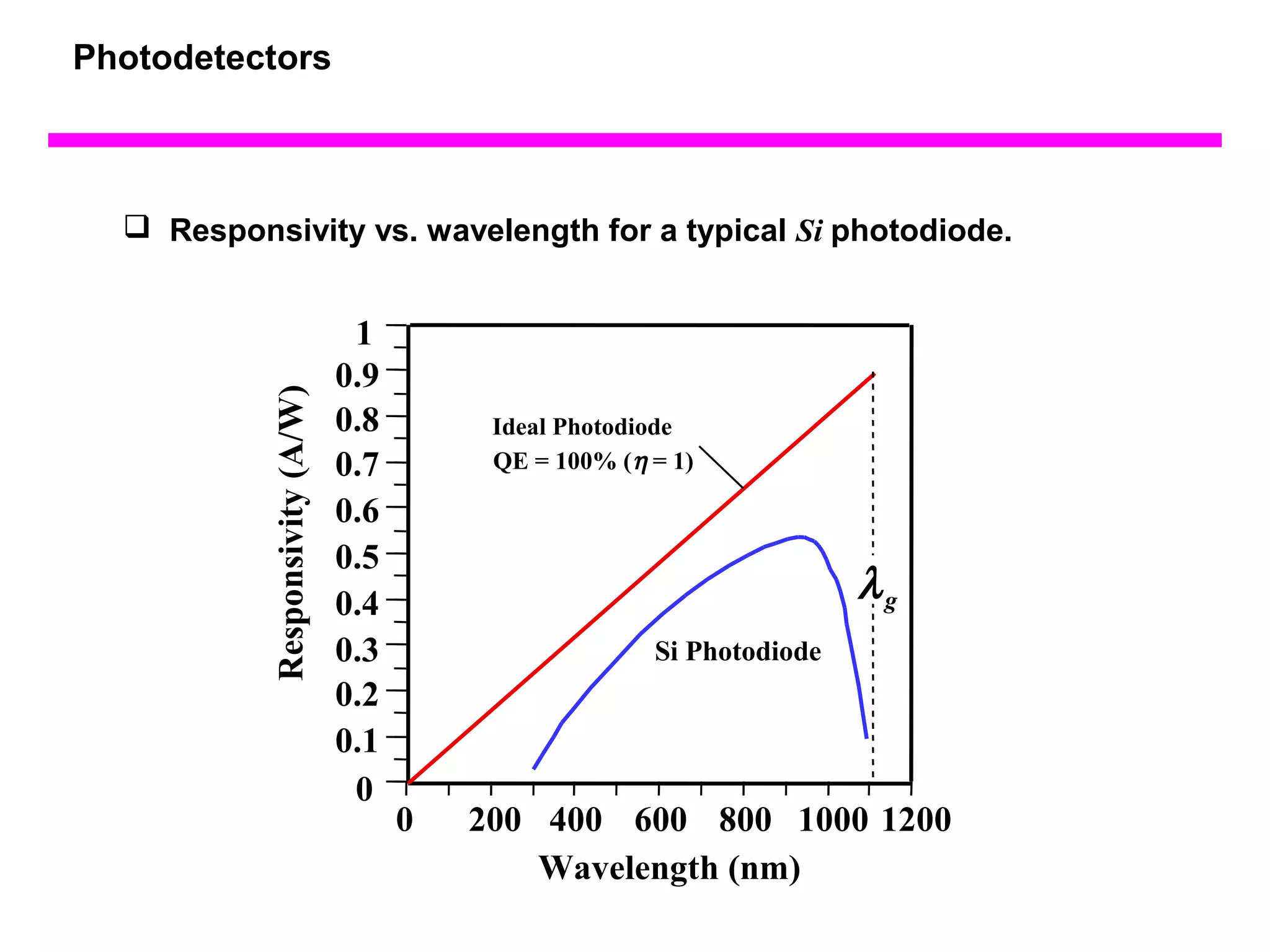
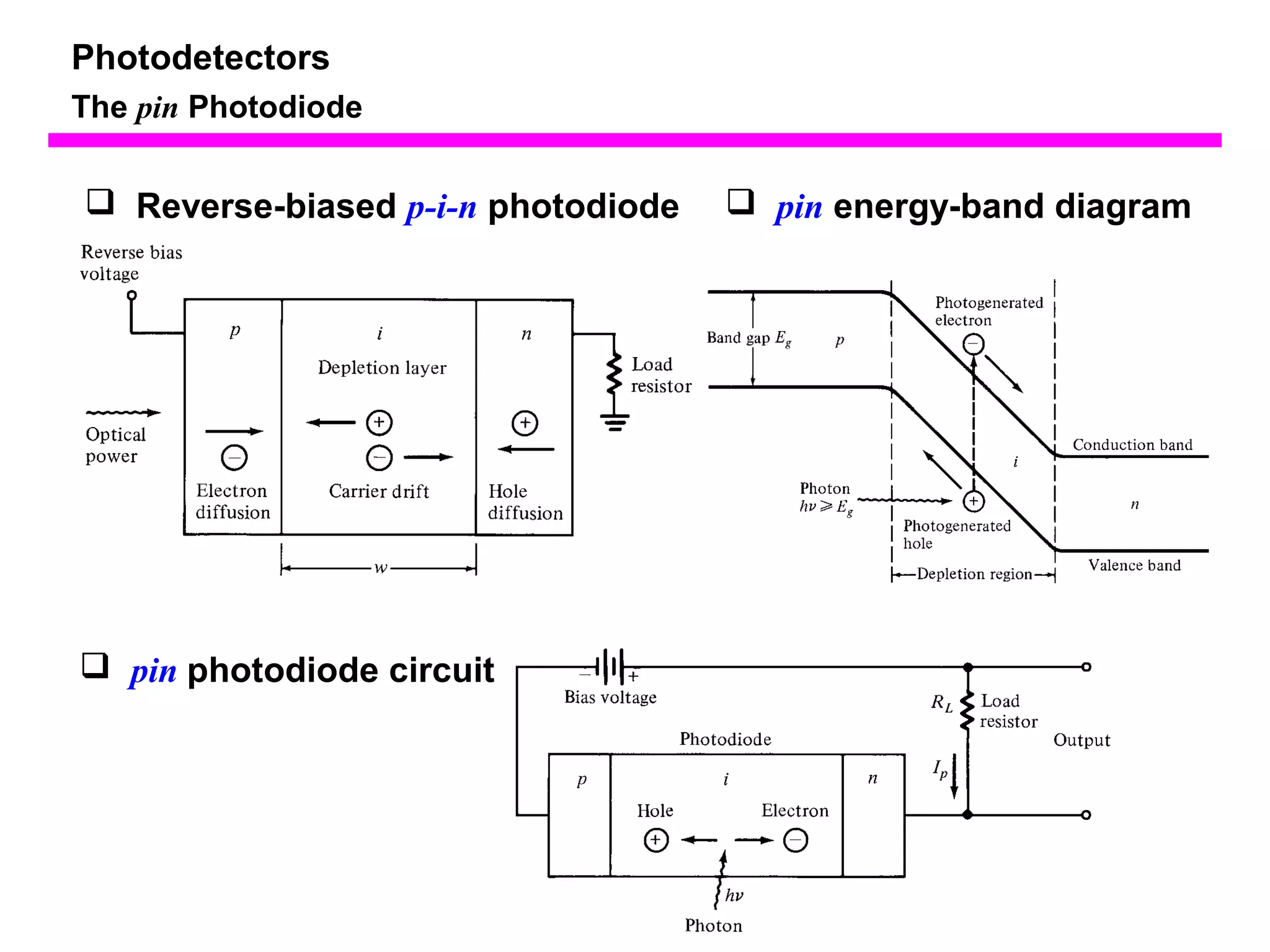
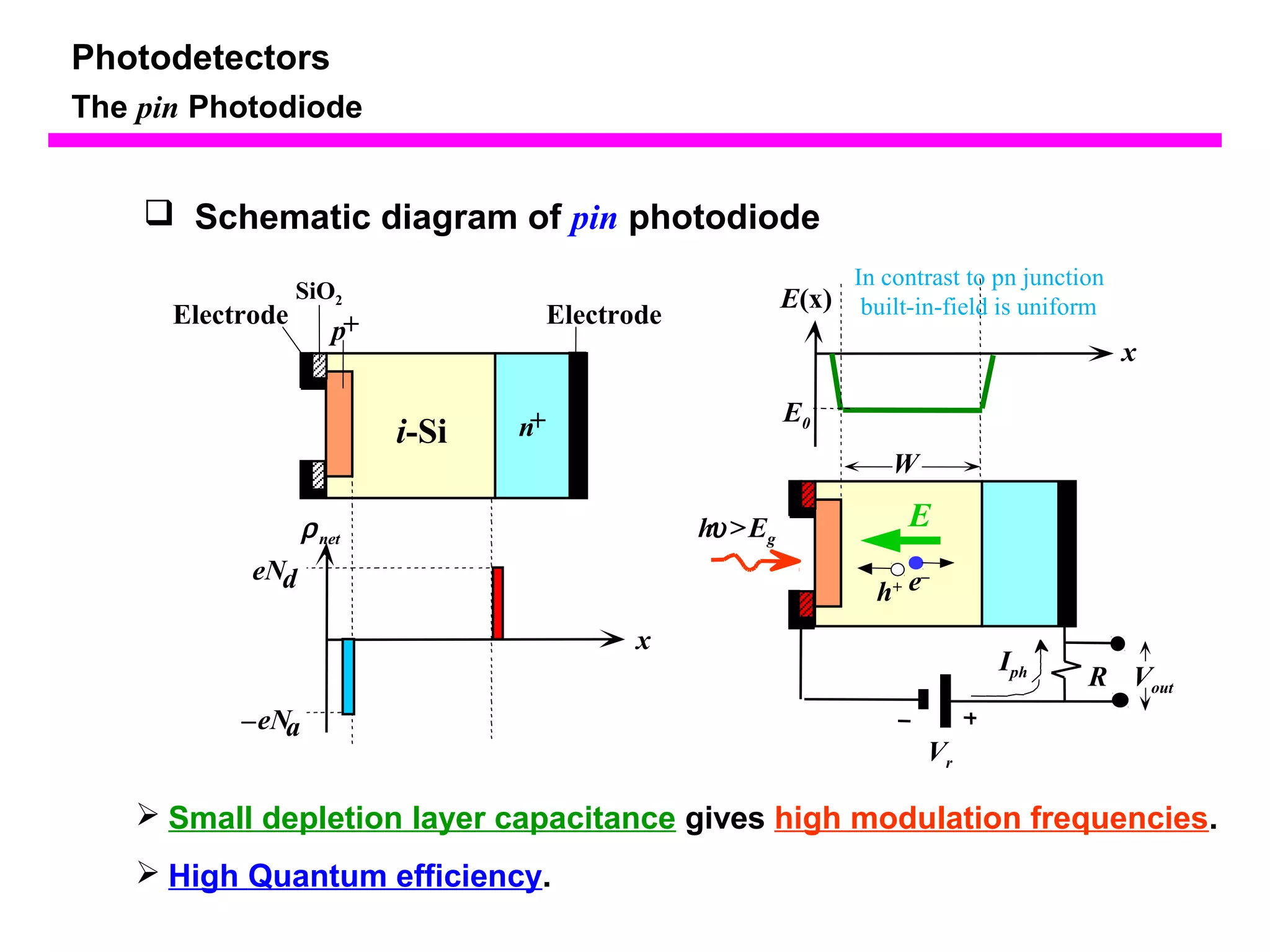
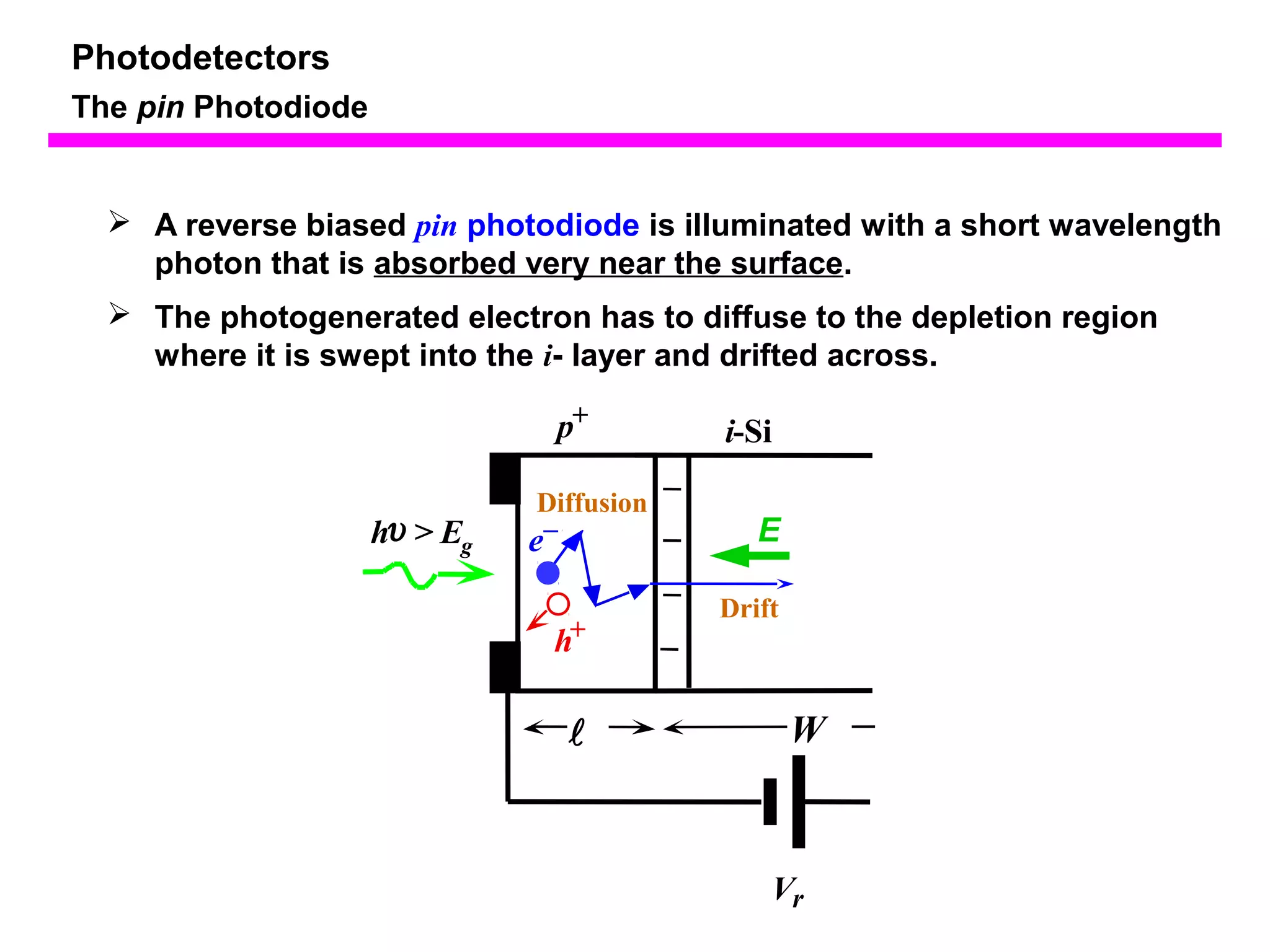
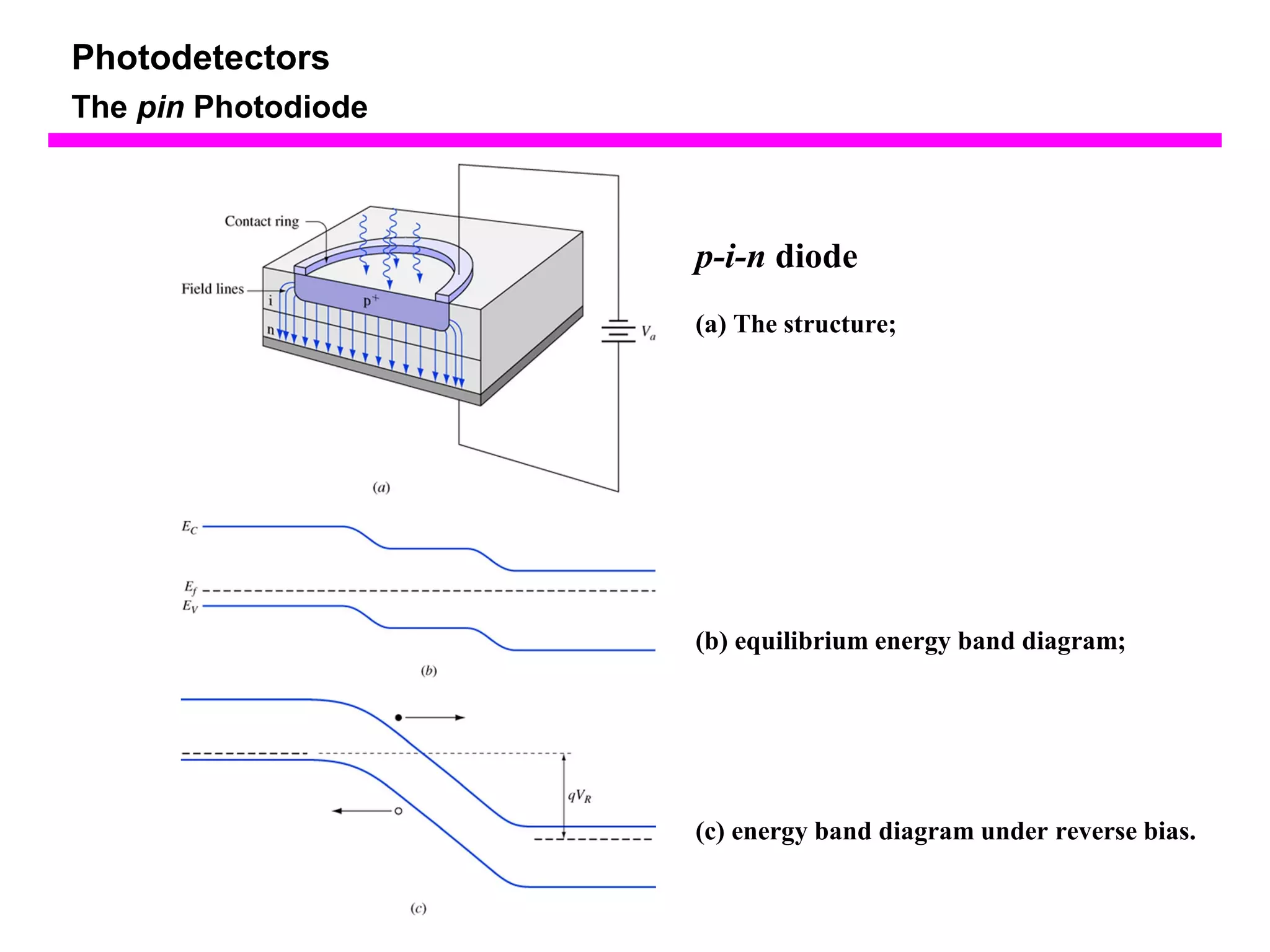
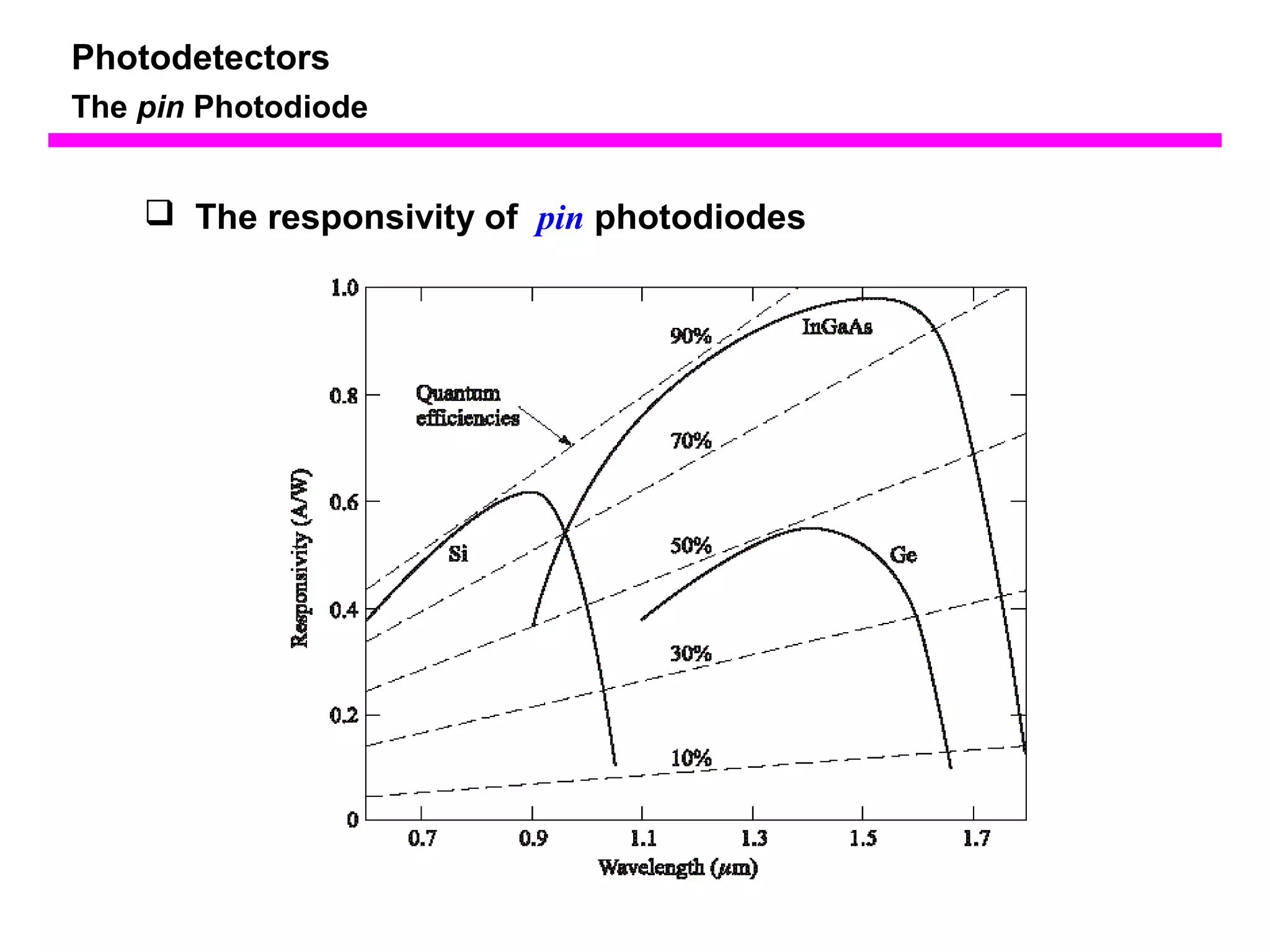
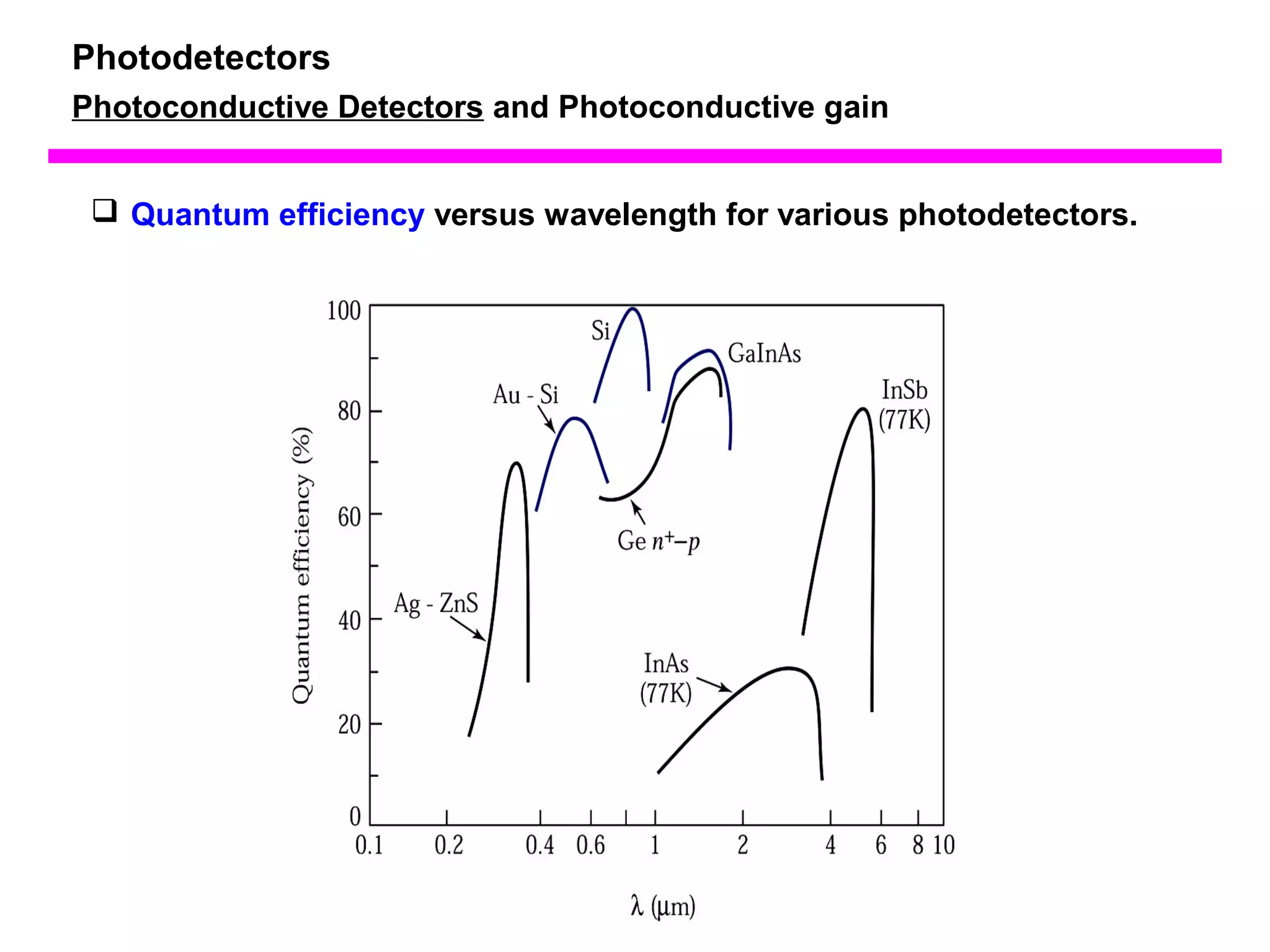
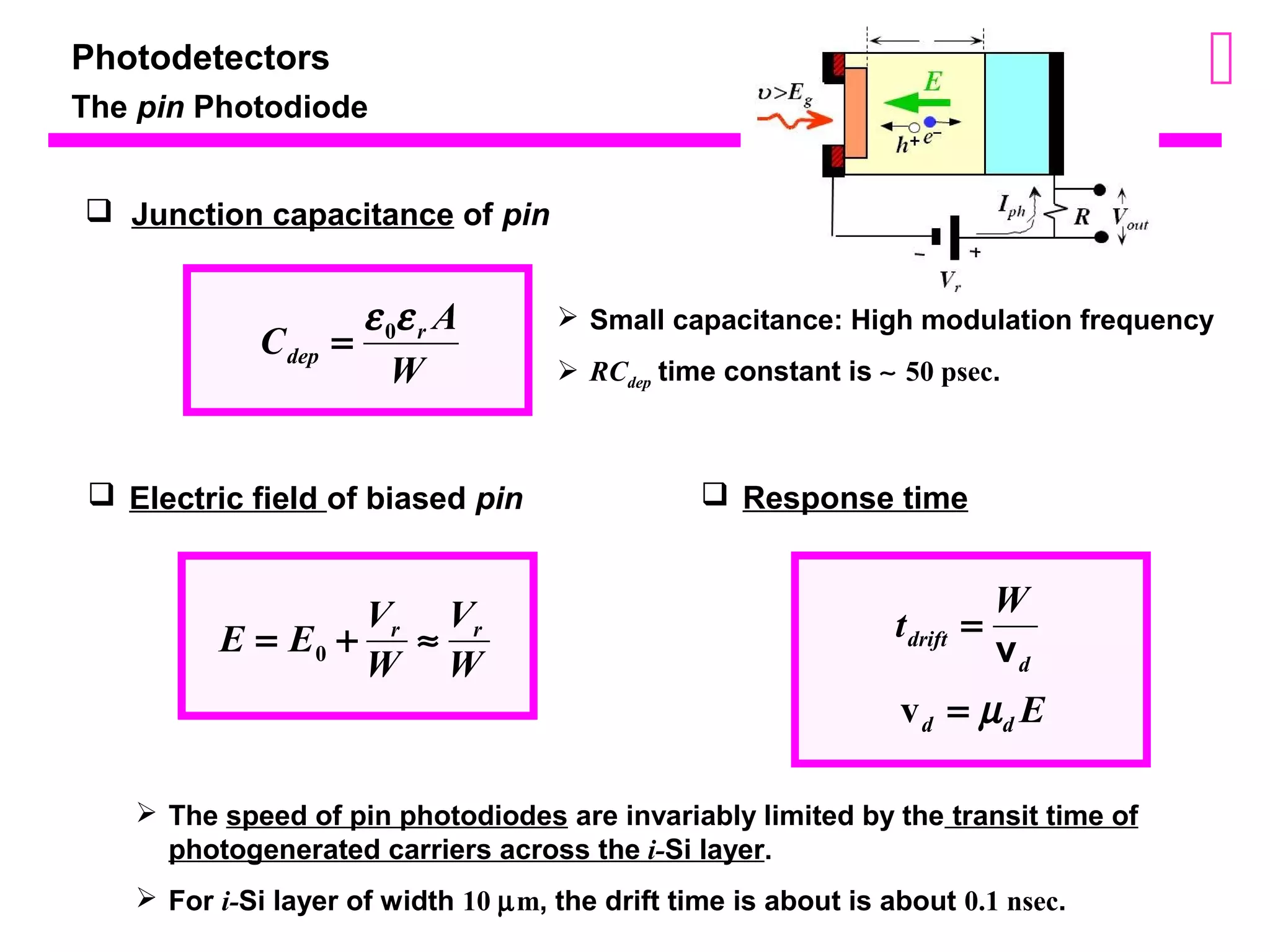
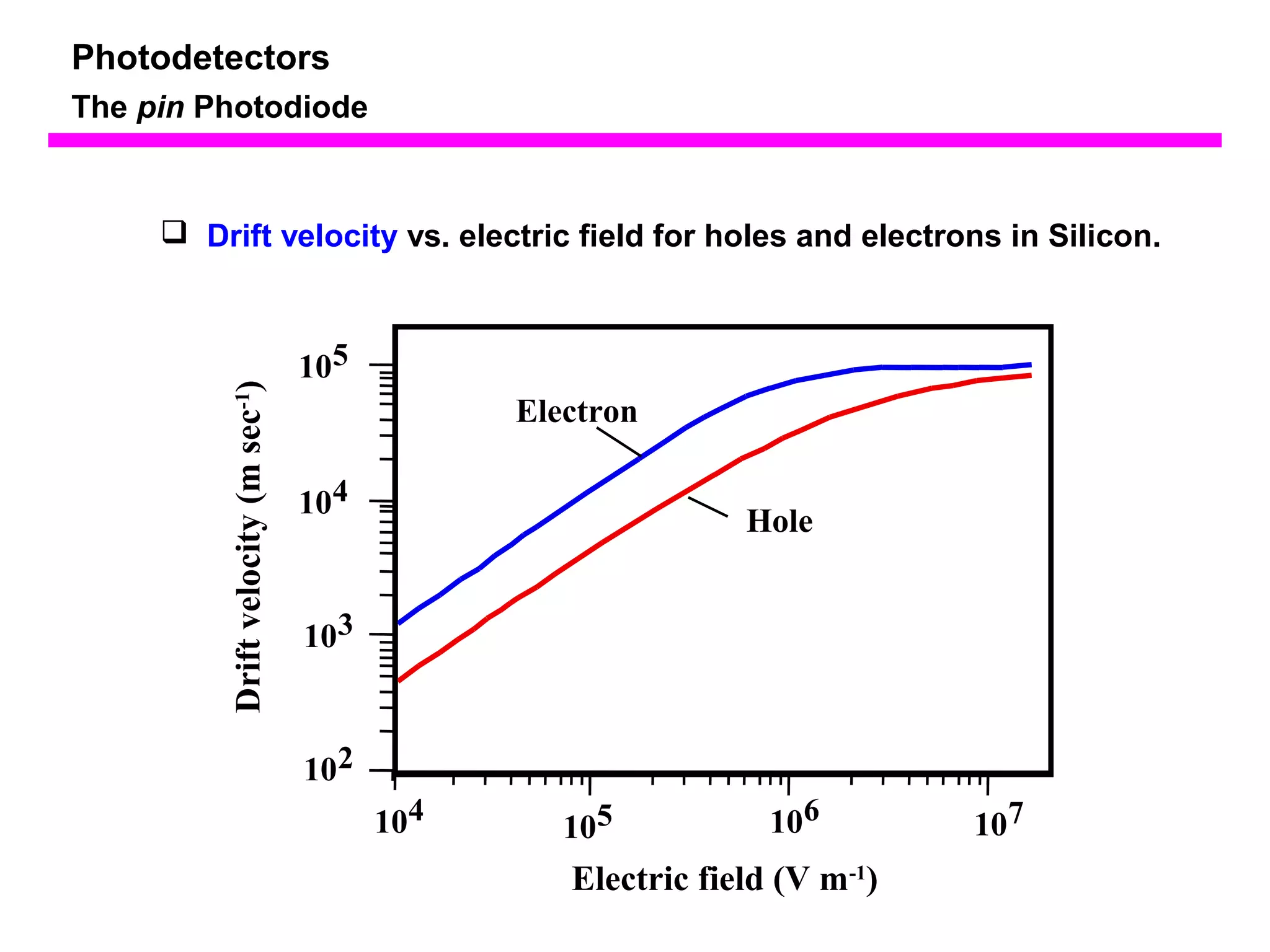
The document discusses photodetectors and the principles of p-n junction photodiodes. It describes the depletion region of a reverse biased p-n junction and how electron-hole pairs generated by photons are separated by the electric field. It also discusses pin photodiodes and how their intrinsic region allows for higher quantum efficiency and modulation frequencies compared to p-n junction photodiodes. Absorption coefficients of various semiconductor materials are shown as well as how direct and indirect bandgap materials differ in photon absorption.

1. Photodetectors

5. Photodetectors
Principle of the p-n junction Photodiode
 Schematic diagram of a reverse
biased p-n junction photodiode
SiO2
Electrode
r net
eNd x
–eNa
x
E (x)
R
E max
h+ e–
Iph
hv > Eg
W
E
n
Depletion
region
AR
coating
Vr
Vout
Electrode
 Net space charge across the diode
in the depletion region. Nd and Na
are the donor and acceptor
concentrations in the p and n
sides.
 The field in the depletion region.
p+
Photocurrent is depend on number
of EHP and drift velocity.
The electrode do not inject carriers
but allow excess carriers in the
sample to leave and become
collected by the battery.

6. 6
Principle of pn junction photodiode
• (a) Reversed biased p+n junction
photodiode.
• Annular electrode to allow photon
to enter the device.
• Antireflection coating (Si3N4) to
reduce the reflection.
• The p+-side thickness < 1 μm.
• (b) Net space charge distribution,
within SCL.
• (c) The E field across depletion
region.

7. Photodetectors
Principle of the p-n junction Photodiode
(b) Energy band diagram under reverse
bias.
(a) Cross-section view of a p-i-n photodiode.
(c) Carrier absorption characteristics.
 Operation of a p-i-n photodiode.

8. Photodetectors
Principle of the p-n junction Photodiode
 A generic photodiode.

9. Photodetectors
Principle of the p-n junction Photodiode
 Variation of photon flux with distance.
A physical diagram showing the depletion
region.
 A plot of the the flux as a function of distance.
 There is a loss due to Fresnel reflection at the surface,
followed by the decaying exponential loss due to absorption.
 The photon penetration depth x0 is defined as the depth at
which the photon flux is reduced to e-1 of its surface value.

10. Photodetectors
RAMO’s Theorem and External Photocurrent
 An EHP is photogenerated at x = l. The electron and the hole drift in opposite directions with
drift velocities vh and ve.
 The electron arrives at time telectron = (L-l )/ve and the hole arrives at time thole = l/vh.
0
t
t t
V
e- h+
Iphoto(t)
Semiconductor
x
l L- l
t
vhole
0 l L
h+ e–
0
e h v
e v e
v
h e ö çè
Area = Charge = e
evh/L eve /L
ielectron(t)
photocurrent
E
L
÷ø
æ L
+ L
thole
telectron
thole ihole(t)
i (t)
telectron
thole
velectron
iphoto(t)

11. Photodetectors
RAMO’s Theorem and External Photocurrent
 As the electron and hole drift, each generates ielectron(t) and ihole(t).
 The total photocurrent is the sum of hole and electron photocurrents each
lasting a duration th and te respectively.
t ( t ) L = - l and t ( t )
l v = v Transit time
Work done = e × E dx = V ×
i ( t ) dt e i ( t ) e v = ; < ( ) e
h
e
L t t
e i t = e v ; <
h
L t t
h E V e = =
Q i ( t ) dt i ( t ) dt e e th
h
t
collected e = ò + ò = 0 0
If a charge q is being drifted with a velocity vd(t) by a field between two biased
electrodes separated by L, the motion of q generates an external current
given by
( )
transit
i (t) = e v t ; <
d t t L
h
h
e
e
v dx
dt
L
Photocurrent
The collected charge is not
2e but just “one electron”.
Ramo’s Theorem


12. Photodetectors
Absorption Coefficient and Photodiode Materials
 Absorbed Photon create Electron-Hole Pair.
[ ] 1.24 m E eV
[ ]
g
g l m =
Cut-off wavelength
vs. Energy bandgap
 Incident photons become absorbed as they travel in the
semiconductor and light intensity decays exponentially
with distance into the semiconductor.
I x = I × e-a x 0 ( ) Absorption coefficient


13. Absorption Coefficient
5 4 3 2 1 0.9 0.8 0.7
13
• Absorption
coefficient α is a
material property.
• Most of the photon
absorption (63%)
occurs over a
distance 1/α (it is
called penetration
depth δ)
GaAs
0.2 0.4 0.6 0.8 1.0
1.2 1.4 1.6 1.8
Wavelength (mm)
In0.53Ga0.47As
Ge
Si
In0.7Ga0.3As0.64P0.36
InP
a-Si:H
1´108
1´107
1´106
a (m-1)
1´105
1´104
1´103
Photon energy (eV)
Absorption coefficient ( a) vs. wavelength (l) for various semiconductors
(Data selectively collected and combined from various sources.)

14. Photodetectors
Absorption Coefficient and Photodiode Materials
54 3 2 1 0.9 0.8 0.7
Ge
GaAs
1´108
1´107
1´106
1´105
1´104
0.2 0.4 0.6 0.8 1.2 1.4 1.6 1.8
Wavelength (mm)
Si
In0.7Ga0.3As0.64P0.36
InP
a-Si:H
1´103
Photon energy (eV)
Absorption Coefficient a (m-1)
1.0
In0.53Ga0.47As
 Absorption
The indirect-gap materials are shown with a broken line.

15. Absorption Coefficient
• Direct bandgap semiconductors
(GaAs, InAs, InP, GaSb, InGaAs,
GaAsSb), the photon absorption does
not require assistant from lattice
vibrations. The photon is absorbed
and the electron is excited directly
from the VB to CB without a change
in its k-vector (crystal momentum
ħk), since photon momentum is very
small.
15
E
CB
Ec
Ev
Direct Bandgap Eg Photon
VB
–k k
(a) GaAs (Direct bandgap)
(a) Photon absorption in a direct bandgap in an indirect bandgap semiconductor © 1999 S.O. Kasap, Optoelectronics (Prentice photon momentum 0 CB VB k - k = »
 Absorption coefficient α for direct bandgap semiconductors
rise sharply with decreasing wavelength from λg (GaAs and
InP).

16. Absorption Coefficient
• Indirect bandgap
semiconductors (Si and Ge), the
photon absorption requires
assistant from lattice vibrations
(phonon). If K is wave vector
of lattice wave, then ħK
represents the momentum
associated with lattice vibration
 ħK is a phonon momentum.
k - k = phonon momentum = K CB VB
16
E
CB
Ec
Ev
Direct Bandgap Eg Photon
VB
–k k
(a) GaAs (Direct bandgap)
E
VB
CB
Indirect Bandgap, Eg
Ec
Ev
Photon
Phonon
–k k
(b) Si (Indirect bandgap)
(a) Photon absorption in a direct bandgap semiconductor. (b) Photon absorption
in an indirect bandgap semiconductor (VB, valence band; CB, conduction band)
© 1999 S.O. Kasap, Optoelectronics (Prentice Hall)
 Thus the probability of photon absorption is not as high as in a
direct transition and the λg is not as sharp as for direct bandgap
semiconductors.

17. Photodetectors
Absorption Coefficient and Photodiode Materials
Photon absorption in
a direct bandgap semiconductor.
E
CB
VB
Direct Bandgap Eg
–k k
Photon absorption in
an indirect bandgap semiconductor
E
VB
CB
Indirect Bandgap
Photon
EE g C
EV
Phonons
–k k
EC
EV
Photon

18. Photodetectors
Quantum Efficiency and Responsivity
I e
 External Quantum Efficiency
Number of EHP geberated and collected ph
h P h
n
Number of incidnet photons
0
= =
I
R = Photocurrent = ph
0 (W)
(A)
P
Incident Optical Power
 Responsivity
R e e
h l
=h = Spectral Responsivity
h c
h
n


19.  Responsivity vs. wavelength for a typical Si photodiode.
Si Photodiode
0 200 400 600 800 1000 1200
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
Wavelength (nm)
l g
Responsivity (A/W)
Ideal Photodiode
QE = 100% ( h = 1)
Photodetectors

20. The pin Photodiode
• The pn junction photodiode has two
drawbacks:
– Depletion layer capacitance is not
sufficiently small to allow
photodetection at high modulation
frequencies (RC time constant
limitation).
– Narrow SCL (at most a few microns) 
long wavelengths incident photons are
absorbed outside SCL  low QE
• The pin photodiode can significantly
reduce these problems.
 Intrinsic layer has less doping and wider region (5 – 50 μm).
20

21. Photodetectors
The pin Photodiode
 Reverse-biased p-i-n photodiode
 pin energy-band diagram
 pin photodiode circuit

22.  Schematic diagram of pin photodiode
SiO2
p+
i-Si n+
Electrode
r net
eNd
–eNa
x
x
E(x)
In contrast to pn junction
built-in-field is uniform
R
E0
e– h+
Iph
hu > Eg
W
Vr
Vout
Electrode
E
Photodetectors
The pin Photodiode
 Small depletion layer capacitance gives high modulation frequencies.
 High Quantum efficiency.

23.  A reverse biased pin photodiode is illuminated with a short wavelength
photon that is absorbed very near the surface.
 The photogenerated electron has to diffuse to the depletion region
where it is swept into the i- layer and drifted across.
hu > Eg
p+ i-Si
Diffusion
e–
h+
E
Drift
 W
Vr
Photodetectors
The pin Photodiode

24. p-i-n diode
(a) The structure;
(b) equilibrium energy band diagram;
(c) energy band diagram under reverse bias.
Photodetectors
The pin Photodiode

25. Photodetectors
The pin Photodiode
 The responsivity of pin photodiodes

26. Photodetectors
Photoconductive Detectors and Photoconductive gain
 Quantum efficiency versus wavelength for various photodetectors.

27. Photodetectors
The pin Photodiode
 Junction capacitance of pin
C = e e A
0
r dep
W
 Electric field of biased pin
 Small capacitance: High modulation frequency
 RCdep time constant is ~ 50 psec.
W V
W V
E = E + r » r 0
 Response time
t Wv =
d
drift
E d d v = m
 The speed of pin photodiodes are invariably limited by the transit time of
photogenerated carriers across the i-Si layer.
 For i-Si layer of width 10 mm, the drift time is about is about 0.1 nsec.


28. Photodetectors
The pin Photodiode
 Drift velocity vs. electric field for holes and electrons in Silicon.
105
104
103
102
Electron
Hole
104 105 106 107
Electric field (V m-1)
Drift velocity (m sec-1)

32. Example
Bandgap and photodetection
(a) Determine the maximum value of the energy gap which a semiconductor, used as a
photoconductor, can have if it is to be sensitive to yellow light (600 nm).
(b) A photodetector whose area is 5´10-2 cm2 is irradiated with yellow light whose
intensity is 20 mW cm-2. Assuming that each photon generates one electron-hole
pair, calculate the number of pairs generated per second.
Solution
(a) Given, l = 600 nm, we need Eph = hu = Eg so that,
Eg = hc/l = (6.626´10-34 J s)(3´108 m s-1)/(600´10-9 m) = 2.07 eV
(b) Area = 5´10-2 cm2 and Ilight = 20´10-3 W/cm2.
The received power is
P = Area ´Ilight = (5´10-2 cm2)(20´10-3 W/cm2) = 10-3 W
Nph = number of photons arriving per second = P/Eph
= (10-3 W)/(2.059´1.60218´10-19 J/eV)
= 2.9787´1015 photons s-1 = 2.9787´1015 EHP s-1.

33. Example
Bandgap and Photodetection
(c) From the known energy gap of the semiconductor GaAs (Eg = 1.42 eV), calculate the
primary wavelength of photons emitted from this crystal as a result of electron-hole
recombination. Is this wavelength in the visible?
(d) Will a silicon photodetector be sensitive to the radiation from a GaAs laser? Why?
Solution
(c) For GaAs, Eg = 1.42 eV and the corresponding wavelength is
l = hc/ Eg = (6.626´10-34 J s)(3´108 m s-1)/(1.42 eV´1.6´10-19 J/eV)
= 873 nm (invisible IR)
The wavelength of emitted radiation due to EHP recombination is 873 nm.
(d) For Si, Eg = 1.1 eV and the corresponding cut-off wavelength is,
lg = hc/ Eg = (6.626´10-34 J s)(3´108 m s-1)/(1.1 eV´1.6´10-19 J/eV)
= 1120 nm
Since the 873 nm wavelength is shorter than the cut-off wavelength of 1120 nm, the
Si photodetector can detect the 873 nm radiation (Put differently, the photon energy
corresponding to 873 nm, 1.42 eV, is larger than the Eg, 1.1 eV, of Si which mean
that the Si photodetector can indeed detect the 873 nm radiation)

34. Example
Absorption coefficient
(a)If d is the thickness of a photodetector material, Io is the intensity of the incoming
radiation, the number of photons absorbed per unit volume of sample is
[ ]
n I d ph
= 1 - exp( - a
×
) 0 d h
u
Solution
(a) If I0 is the intensity of incoming radiation (energy flowing per unit area per
second), I0 exp(-a d ) is the transmitted intensity through the specimen with
thickness d and thus I0 exp(-a d ) is the “absorbed” intensity

35. Example
(b) What is the thickness of a Ge and In0.53Ga0.47As crystal layer that is needed for
absorbing 90% of the incident radiation at 1.5 mm?
For Ge, a » 5.2 ´ 105 m-1 at 1.5 mm incident radiation.
For In0.53Ga0.47As, a » 7.5 ´ 105 m-1 at 1.5 mm incident radiation.
For Ge, a » 5.2 ´ 105 m-1 at 1.5 mm incident radiation.
d
ln 1
1
1 exp( ) 0.9
- - × =
1 ln 1
çè
æ
ö d m m
m
a
a
4.428 10 4.428
1 0.9
5.2 10
1 0.9
6
5 = ´ = ÷ø
´ -
æ
ö = ÷ø-
çè
=
-
For In0.53Ga0.47As, a » 7.5 ´ 105 m-1 at 1.5 mm incident radiation.
1 6
ln 1
çè
æ
ö = -
d 3.07 10 m 3.07mm
1 0.9
7.5 10
5 = ´ = ÷ø
´ -
(b)

36. Example
InGaAs pin Photodiodes
Consider a commercial InGaAs pin photodiode whose responsivity is shown in fig.
Responsivity (A/W)
1
0.8
0.6
0.4
0.2
0
800 1000 1200 1400 1600 1800
Wavelength (nm)
 The responsivity of an InGaAs
pin photodiode
Its dark current is 5 nA.
(a) What optical power at a wavelength of 1.55 mm would give a photocurrent
that is twice the dark current? What is the QE of the photodetector at 1.55
mm?
(b) What would be the photocurrent if the incident power in a was at 1.3 mm?
What is the QE at 1.3 mm operation?

37. Solution
(a) At l = 1.55´10-6 m, from the responsivity vs. wavelength curve we
have R » 0.87 A/W. From the definition of responsivity,
we have
I
R = Photocurrent A = ph
P
Incident Optical Power W
( ) 0
( )
nW
2 2 5 10 -
9 ( )
0 = = = ´ ´ =
P ph dark 11.5
A W
A
I
R
I
R
0.87 / )
From the definitions of quantum efficiency h and responsivity,
R e e
h l
hc
=h =
h
u
0.70 (70%)
34 8
-
J m s A W
(6.62 10 sec)(3 10 / )(0.87 / )
hcR
l
= = ´ × ´ - -
19 6
coul m
(1.6 10 )(1.55 10 )
=
´ ´
e
h
Note the following dimensional identities: A = C s-1 and W = J s-1 so that A W-1 = C J-1.
Thus, responsivity in terms of photocurrent per unit incident optical power is also charge
collected per unit incident energy.

38. Solution
(b) At l = 1.3´10-6 m, from the responsivity vs. wavelength curve, R = 0.82 A/W.
Since Po is the same and 11.5 nW as in (a),
The QE at l = 1.3 mm is
0.78 (78%)
34 8
J m s A W
(6.62 10 sec)(3 10 / )(0.82 / )
hcR
l
= = ´ × ´ - -
19 6
(1.6 10 )(1.3 10 )
»
´ ´
-
coul m
e
h
I R P A W nW nA ph (0.82 / )(1.15 ) 9.43 0 = × = =

39. Photodetectors
Avalanche Photodiode (APD)
p p+
Electrode SiO2
rnet
x
x
E(x)
R
hu > Eg
p
Iphoto
e – h+
Absorptio
n
Avalanche regrieognion
Electrode
n+
E
 Impact ionization processes
resulting avalanche multiplication
h+
e–
E
n+ p p
Avalanche region
e-h+
Ec
Ev
 Impact of an energetic electron's kinetic energy
excites VB electron to the CV.

40. SiO2
Guard ring
Electrode
Antireflection coating
n n n +
p
p
p+
Substrate
Electrode
n+
p
p
p+
Substrate
Electrode
Avalanche breakdown
Si APD structure without a
guard ring
More practical Si APD
Photodetectors
Avalanche Photodiode (APD)
 Schematic diagram of typical Si APD.
 Breakdown voltage around periphery is higher and avalanche is
confined more to illuminated region (n+p junction).

41. Photodetectors
Heterojunction Photodiode
Separate Absorption and Multiplication (SAM) APD
InGaAs-InP heterostructure Separate Absorption and Multiplication APD
E
Vr
N n
Electrode
x
E(x)
R
hu
I
ph
Absorption
region
Avalanche
region
InP InGaAs
h+
e–
InP
P + n+
Vout
E
P and N refer to p- and
n-type wider-bandgap
semiconductor.

42. Photodetectors
Heterojunction Photodiode
Separate Absorption and Multiplication (SAM) APD
InP
InGaAs
e–
h+
Ec
Ev
Ec
Ev
InP
InGaAs
Ev
Ev
h+
DEv
E
InGaAsP grading layer
(a) Energy band diagram for a SAM
heterojunction APD where there is
a valence band step DEv from
InGaAs to InP that slows hole
entry into the InP layer.
(b) An interposing grading layer
(InGaAsP) with an intermediate
bandgap breaks DEv and makes it
easier for the hole to pass to the InP
layer.

43. x
Photogenerated electron concentration
exp( -a x) at time t = 0
R
v
de
A B
e–
h+
i
ph
hu > E
g
W
V
r
E