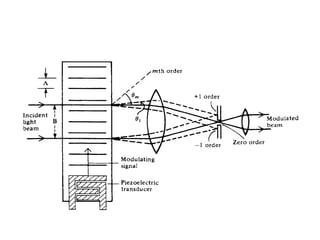
This document discusses magneto-optic and acousto-optic effects. It explains that the Faraday effect causes a rotation of the plane of polarization of light passing through a material under a magnetic field. This effect is used in optical isolators. The document also discusses using magneto-optics for computer memory storage. It then explains that the acousto-optic effect causes a change in refractive index from strain waves, creating a diffraction grating. This can diffract light into different orders depending on the Raman-Nath or Bragg regime.

1. Magneto optic and Acousto optic effect
Unit-IV
Prepared by
S.Vijayakumar, AP/ECE
Ramco Institute of Technology
Academic year
(2017-2018 odd sem)

2. MAGNETO-OPTIC DEVICES
• The presence of magnetic field may also affect
the optical properties of some substances
thereby giving rise to a number of useful
devices

3. FARADAY EFFECT
• It concerns the change in refractive index of a
material s
• when a beam of plane polarized light passes
through a substance subjected to a magnetic
field, its plane of polarization is observed to
rotate by an amount proportional to the
magnetic field component parallel to the
direction of propagation. subjected to a
steady magnetic field

4. • The rotation of the plane of polarization is
given by
• 𝜃 = 𝑉𝑉𝑉 −−−− −(1)
• We can also express interms of refractive
indices 𝑛 𝑟 and 𝑛𝑙, that is
• 𝜃 =
𝜋
𝜆0
(𝑛 𝑟 − 𝑛𝑙)𝐿

5. • A Faraday rotator used in conjunction with a
pair of polarizers acts as an optical isolator
which allows a light beam to travel through it
in one direction but not in the opposite one

6. • The construction of a typical isolator is shown
in below figure.

7. Application
• One potential application of magneto-optics
currently receiving attention is large capacity
computer memories. Such memories must be
capable of storing very large amounts of
information in a relatively small area and
permit very rapid readout and preferably,
random access

8. • Writing may be achieved by heating the
memory elements on the storage medium to a
temperature above the Curie point using a
laser beam.
• The element is allowed to cool down in the
presence of an external magnetic field thereby
acquiring a magnetization in a given direction.

9. • Magnetizations of the elements in one
direction may represent ‘ones’, in the opposite
direction ‘zeros’.

10. • To read the information the irradiance of the
laser beam is reduced and then directed to
the memory elements.
• The direction of the change in the
polarization of the laser beam on passing
through or being reflected from the memory
elements depends on the directions of
magnetization; therefore we can decide if a
given element is storing a ‘one’ or ‘zero’.

11. ACOUSTO-OPTIC EFFECT
• The acousto-optic effect is the change in
refractive index of a medium caused by the
mechanical strains accompanying the passage
of surface acoustic (strain) wave along the
medium.
• The refractive index varies periodically with a
wavelength λ equal to that of the acoustic
wave.

13. • the acoustic wave sets up a diffraction grating
within the medium so that optical energy is
diffracted out of the incident beam into the
various orders.
• There are two main cases (a) The Raman-Nath
regime and (b) the Bragg regime.

14. • In the Raman-Nath regime the acousting
diffraction grating is so thin.
• The light is diffracted from a simple plane
grating such that
• 𝑚𝑚 = ∆𝑠𝑠𝑠𝜃 𝑚 −−−− −(1)
• Where m=0,±1, ±2, … .is the order and 𝜃 𝑚 is
the corresponding angle of diffraction, as
illustrated in below figure

16. • The fraction of light removed from the zero-
order beam is
• 𝜂 = 𝐼0 − 𝐼 𝐼0⁄
• Where I0 is the transmitted irradiance in the
absence of the acoustic wave.

17. Bragg regime a ‘thick’ diffraction
grating.

18. • constructive interference occurs. The
conditions to be satisfied are:
• Light scattered from a given grating plane
must arrive in phase at the new wavefront and
• Light scattered from successive grating planes
must also arrive in phase at the new
wavefront, imlying that the path difference
must be an integral number of wavelengths.

19. • he first of these condition is satisfied when
𝜃 𝑑 = 𝜃𝑖, where 𝜃 𝑑 is the angle of diffraction.
The second condition requires that
• 𝑠𝑠𝑠𝜃𝑖 + 𝑠𝑠𝑠𝜃 𝑑 = 𝑚𝑚 ∆⁄
• With m=0,1,2…. The two conditions nare
simultaneously fulfilled when
• 𝑠𝑠𝑠𝜃𝑖 = 𝑠𝑠𝑠𝜃 𝑑 = 𝑚𝑚 2∆⁄ −− −(2)

20. • scattering only takes place when m=1. This is
shown in above figure. The equation called Bragg
angle θB becomes
• 𝑠𝑠𝑠𝜃 𝐵 = 𝜆 2∆⁄ −−− −(3)
• At the Bragg angle, η is given by
• η = sin2
φ 2⁄ −−− −(4)
• Where 𝜑 = 2𝜋 𝜆⁄ (∆𝑛𝑛 𝑐𝑐𝑐𝜃 𝐵⁄ ), in which ∆𝑛 is
the amplitude of the refractive index fluctuation,
L the length of the modulator