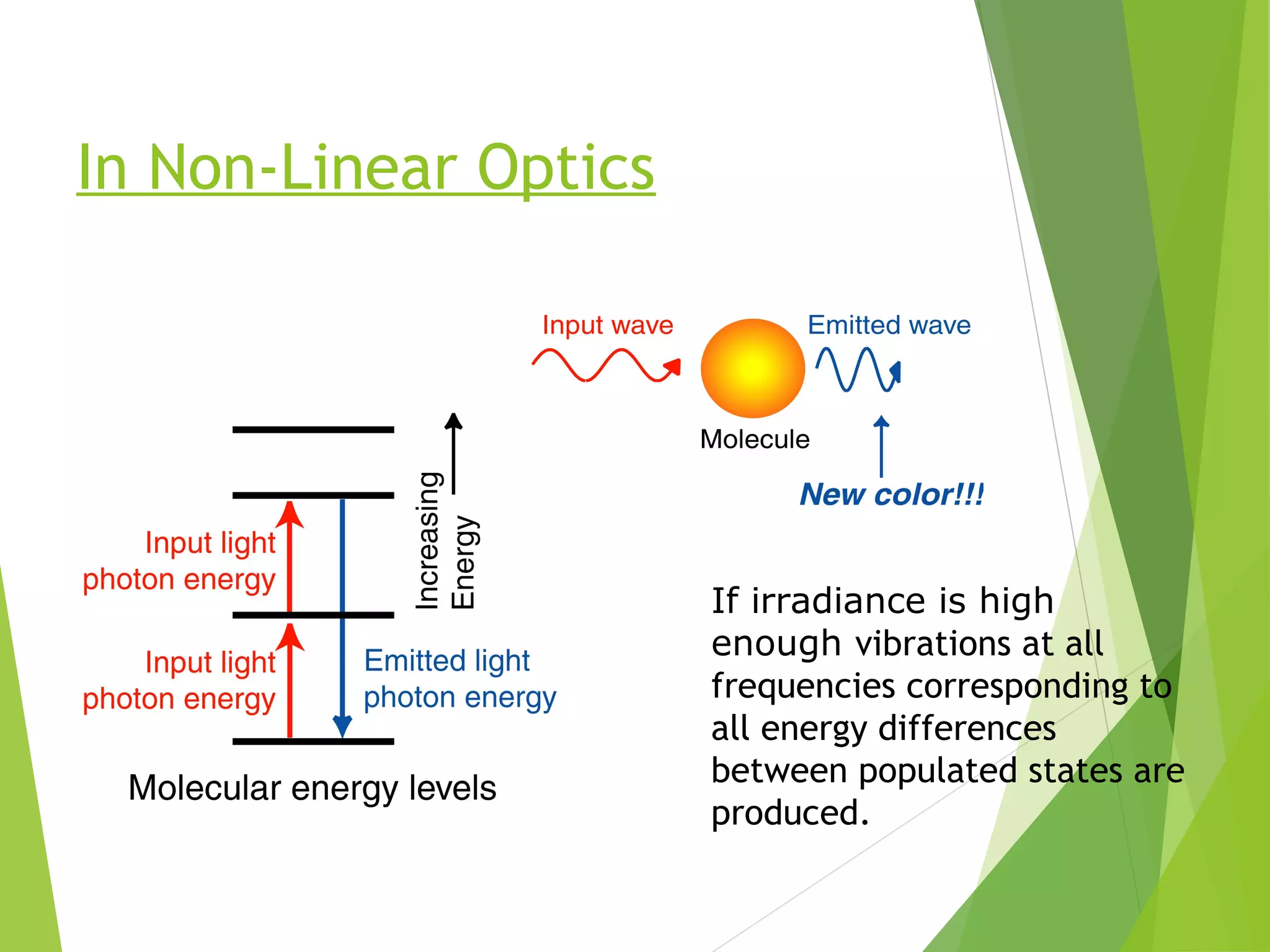
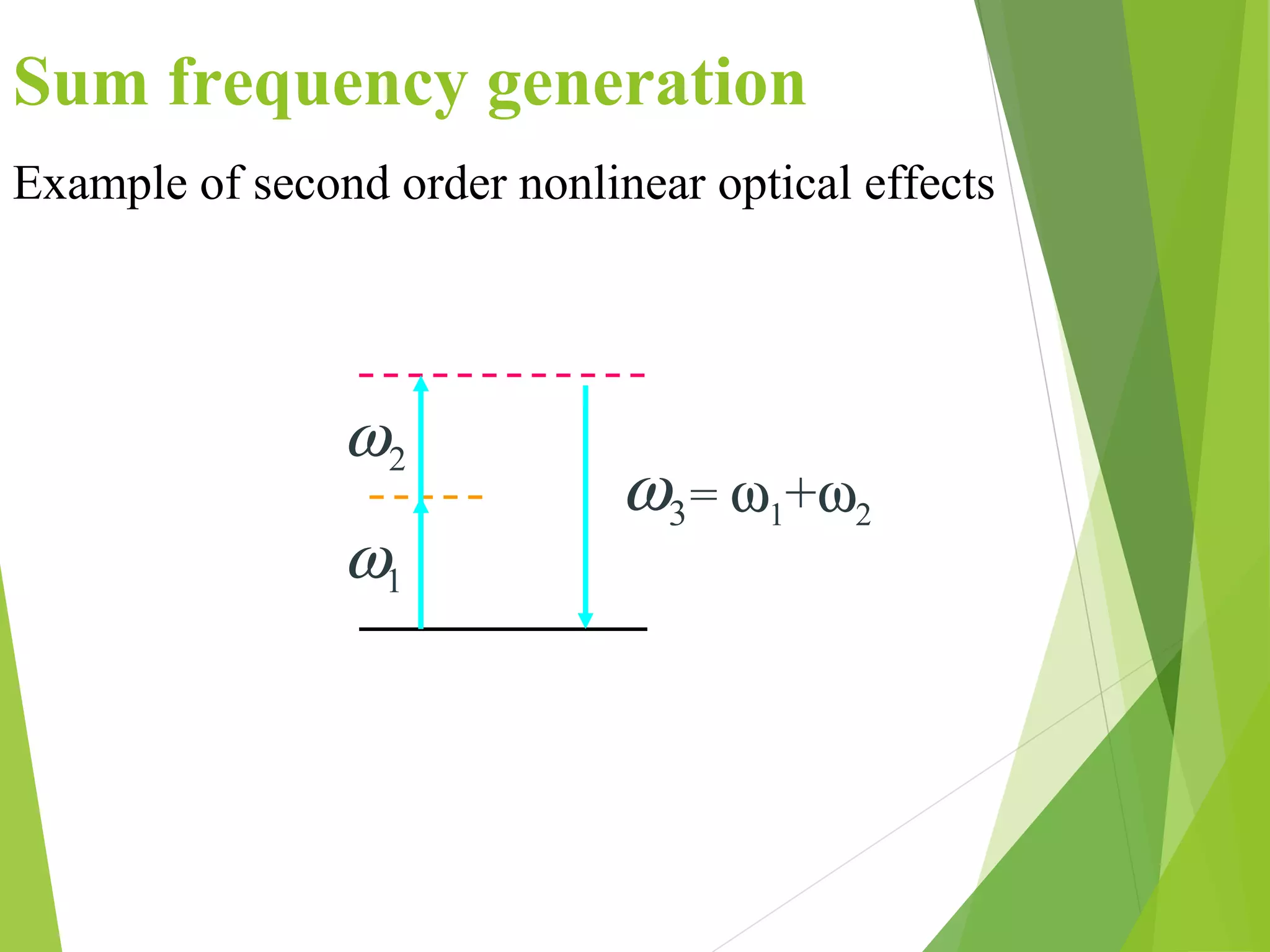
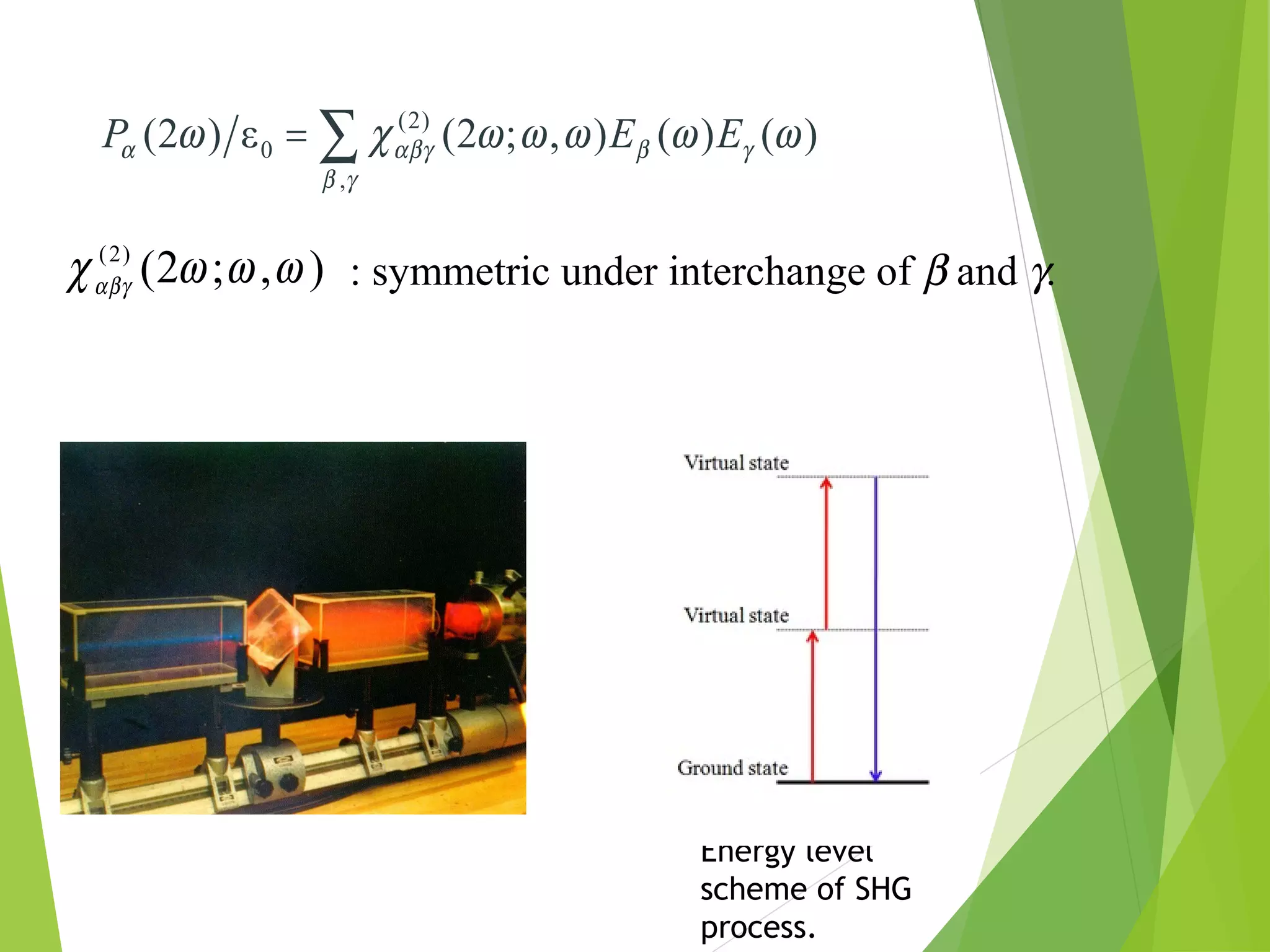
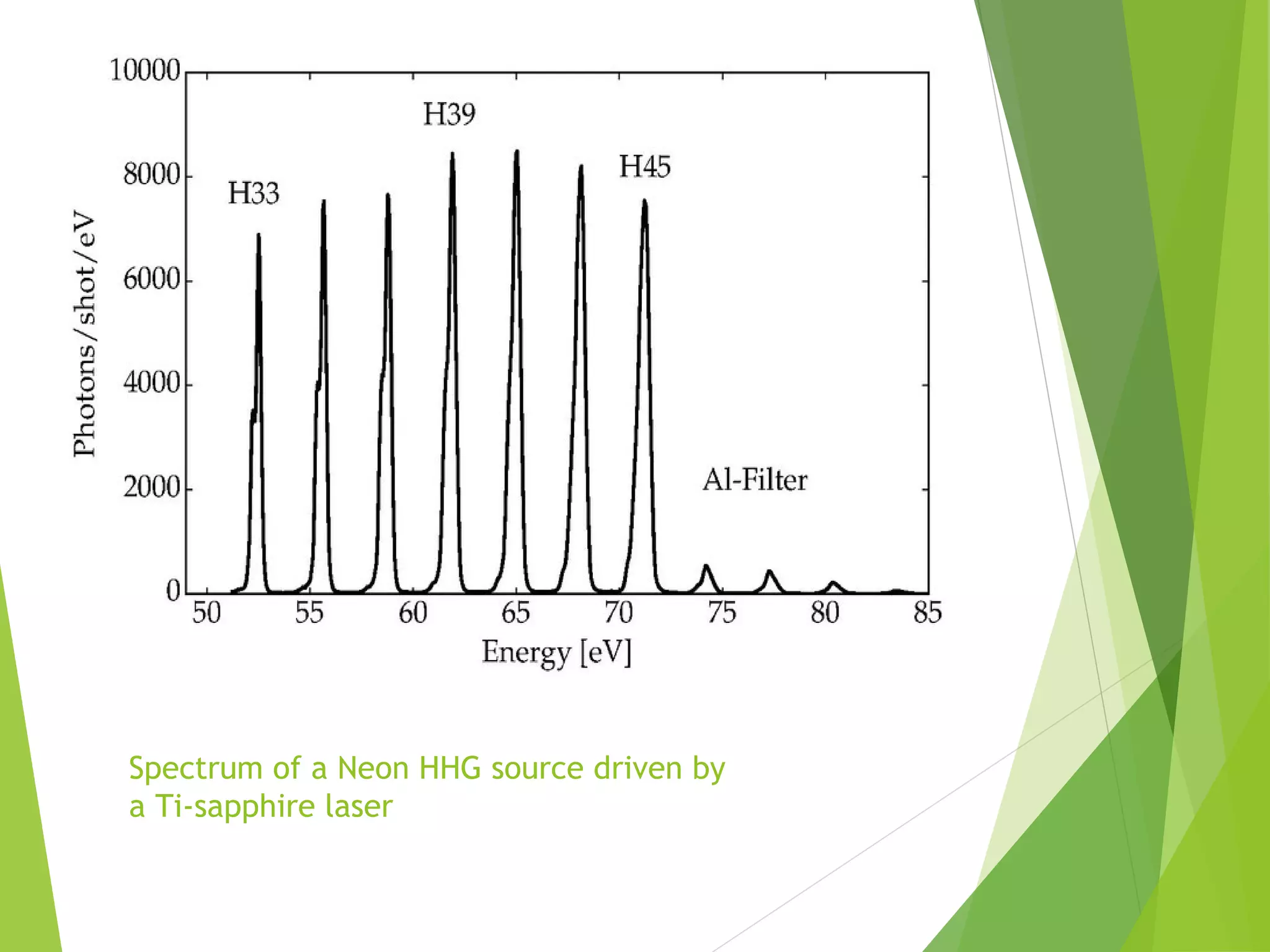
Nonlinear optics involves intense light interacting with matter to change the light's properties. This allows generating new frequencies of light from the input light. Second harmonic generation produces light with twice the frequency by combining two photons. High harmonic generation using intense lasers can generate coherent x-rays. Phase matching is important for high conversion efficiency in nonlinear optical processes. Applications include optical switching, data storage, and generating coherent x-rays for attosecond science.















![OPTICAL MIXING
The generation of new frequencies with help of nonlinear phenomena is called
optical mixing. Suppose two coherent waves of unequal frequencies, ω1 and ω2
are traversing the material, then
E = E1 cos ω1 t + E2 cos ω2 t
Hence
The second term gives rise to 2ω2. The last term can be expressed as
2ε0 χ2 E1 E2 cos ω1t = ε0 χ2 E1 E2 [cos (ω1 + ω2) t + cos (ω1 – ω2) t]
Thus waves of frequencies ω1, 2ω1, ω2, 2ω2, (ω1+ω2) and (ω1–ω2) are
generated. Using proper optical arrangement it is possible to get sufficiently
intense output at any one of these frequencies.](https://image.slidesharecdn.com/nonlinearopticsedited-170407154552/75/Non-linear-optics-and-SHG-20-2048.jpg)


