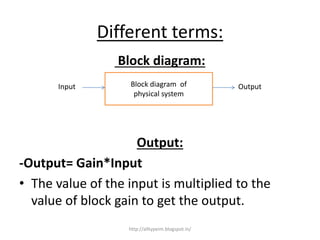
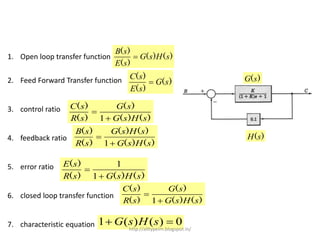
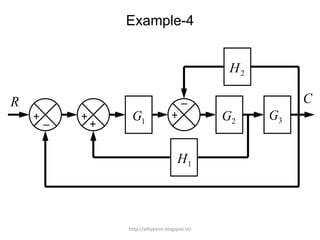
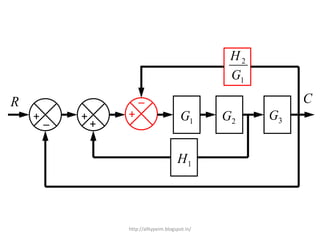
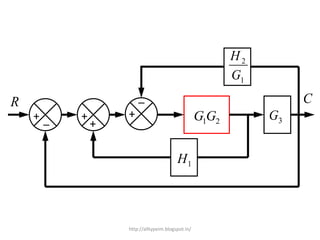
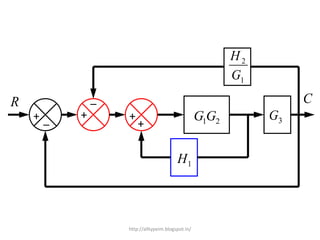
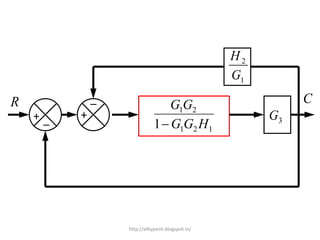
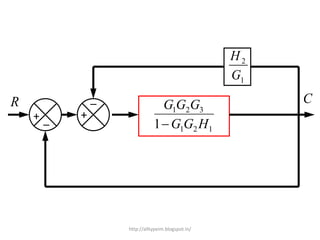
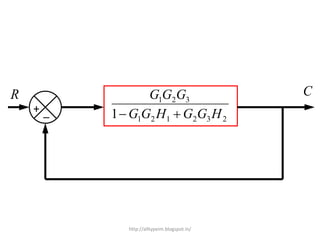
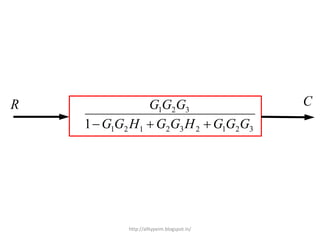
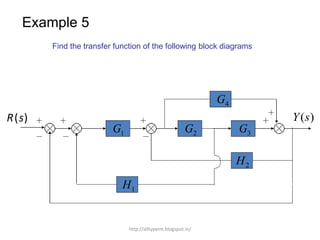
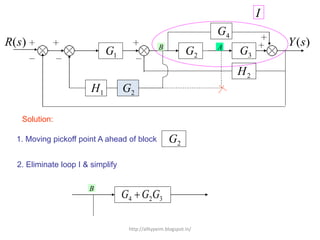
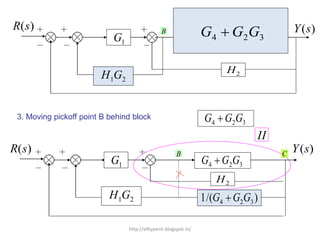
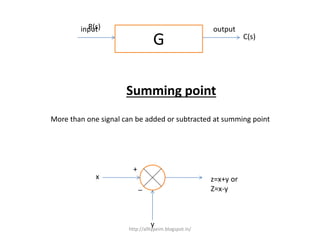
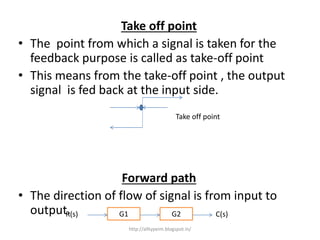
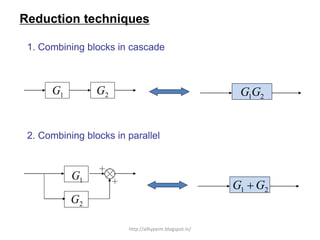
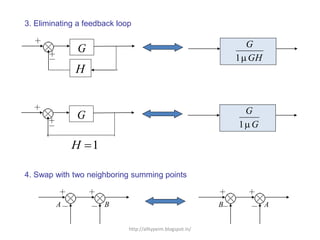
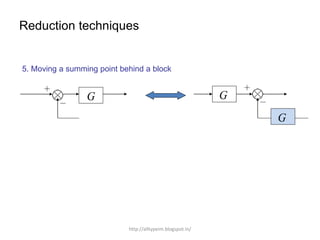
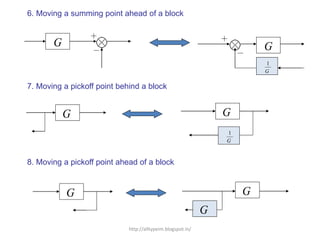
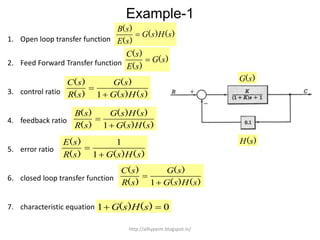
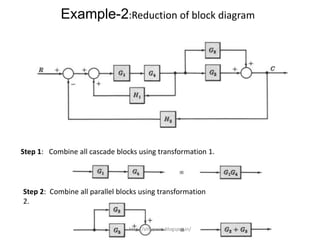
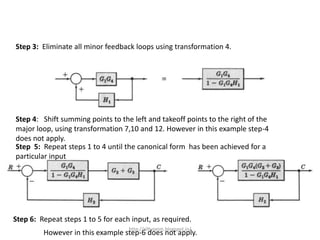
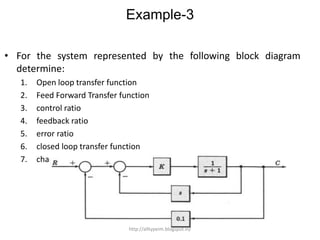
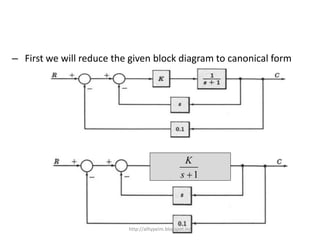
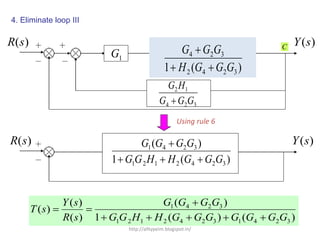
1. A block diagram is a pictorial representation of a system that shows the relationship between inputs and outputs of the entire system. 2. Block diagrams can represent physical systems and use symbols like summing points, gains, and transfer functions. 3. Reduction techniques can be used to simplify block diagrams, such as combining blocks in series or parallel or eliminating feedback loops.

1. BLOCK DIAGRAM
http://alltypeim.blogspot.in/

2. BLOCK DIAGRAM:
o Defination:
1. A block diagram is a pictorial representation
of the entire system.
2. The block diagram represents the
relationship between the input and the
output of the entire system.
http://alltypeim.blogspot.in/

3. Different terms:
Block diagram:
Output:
-Output= Gain*Input
• The value of the input is multiplied to the
value of block gain to get the output.
Block diagram of
physical system
OutputInput
http://alltypeim.blogspot.in/

4. G
R(s)input output
C(s)
Summing point
More than one signal can be added or subtracted at summing point
x
y
z=x+y or
Z=x-y
+
_
http://alltypeim.blogspot.in/

5. Take off point
• The point from which a signal is taken for the
feedback purpose is called as take-off point
• This means from the take-off point , the output
signal is fed back at the input side.
Forward path
• The direction of flow of signal is from input to
output.
Take off point
G1 G2R(s) C(s)
http://alltypeim.blogspot.in/

6. Feedback path
• The direction of flow of signal is from output
to input. It is shown in figure.
GR(S)
+
_
C(S)
Feed back
pathhttp://alltypeim.blogspot.in/

7. Advantages of block diagram
• The functional operation of the system can be
observed from block diagram.
• Block diagram gives the information about
performance of system.
• Block diagram is used for analysis and design
of control system.
• It is very simple to construct the block diagram
for big and complicated system.
http://alltypeim.blogspot.in/

8. Disadvantages of block diagram
• Block diagram for a given system is not unique.
• Source of energy in the system is not shown in
the diagram.
• In the procedure of reduction of block diagram
algebra, some important functions may be
omitted or hidden.
• The block diagram does not give any information
about the physical construction of the system.
http://alltypeim.blogspot.in/

9. Reduction techniques
2G1G 21GG
1. Combining blocks in cascade
1G
2G
21 GG 
2. Combining blocks in parallel
http://alltypeim.blogspot.in/

10. 3. Eliminating a feedback loop
G
H
GH
G
1
4. Swap with two neighboring summing points
A B AB
G
1H
G
G
1
http://alltypeim.blogspot.in/

11. Reduction techniques
5. Moving a summing point behind a block
G G
G
http://alltypeim.blogspot.in/

12. 8. Moving a pickoff point ahead of a block
G G
G G
G
1
G
6. Moving a summing point ahead of a block
G G
G
1
7. Moving a pickoff point behind a block
http://alltypeim.blogspot.in/

13. A Feedback Control System
G=direct transfer function = forward transfer function
H=feedback transfer function
GH=loop transfer function=open-loop transfer function
C/R=closed –loop transfer function= control ratio C
E/R=actuating signal ratio =error ratio
B/R=primary feedback ratio
R
R
=
G
1+_ GH
E 1
1+_ GH
B
R
=
=
GH
1+_ GH
http://alltypeim.blogspot.in/

14. Characteristic Equation
• The control ratio is the closed loop transfer function of the system.
• The denominator of closed loop transfer function determines the
characteristic equation of the system.
• Which is usually determined as:
)()(
)(
)(
)(
sHsG
sG
sR
sC


1
01  )()( sHsG
http://alltypeim.blogspot.in/

15. Example-1
1. Open loop transfer function
2. Feed Forward Transfer function
3. control ratio
4. feedback ratio
5. error ratio
6. closed loop transfer function
7. characteristic equation
)()(
)(
)(
sHsG
sE
sB

)(
)(
)(
sG
sE
sC

)()(
)(
)(
)(
sHsG
sG
sR
sC


1
)()(
)()(
)(
)(
sHsG
sHsG
sR
sB


1
)()()(
)(
sHsGsR
sE


1
1
)()(
)(
)(
)(
sHsG
sG
sR
sC


1
01  )()( sHsG
)(sG
)(sH
http://alltypeim.blogspot.in/

16. Example-2:Reduction of block diagram
Step 1: Combine all cascade blocks using transformation 1.
Step 2: Combine all parallel blocks using transformation
2.
http://alltypeim.blogspot.in/

17. However in this example step-6 does not apply.
Step 3: Eliminate all minor feedback loops using transformation 4.
Step 4: Shift summing points to the left and takeoff points to the right of the
major loop, using transformation 7,10 and 12. However in this example step-4
does not apply.
Step 5: Repeat steps 1 to 4 until the canonical form has been achieved for a
particular input
Step 6: Repeat steps 1 to 5 for each input, as required.
http://alltypeim.blogspot.in/

18. Example-3
• For the system represented by the following block diagram
determine:
1. Open loop transfer function
2. Feed Forward Transfer function
3. control ratio
4. feedback ratio
5. error ratio
6. closed loop transfer function
7. characteristic equation
http://alltypeim.blogspot.in/

19. – First we will reduce the given block diagram to canonical form
1s
K
http://alltypeim.blogspot.in/

20. 1s
K
s
s
K
s
K
GH
G
1
1
1
1




http://alltypeim.blogspot.in/

21. 1. Open loop transfer function
2. Feed Forward Transfer function
3. control ratio
4. feedback ratio
5. error ratio
6. closed loop transfer function
7. characteristic equation
)()(
)(
)(
sHsG
sE
sB

)(
)(
)(
sG
sE
sC

)()(
)(
)(
)(
sHsG
sG
sR
sC


1
)()(
)()(
)(
)(
sHsG
sHsG
sR
sB


1
)()()(
)(
sHsGsR
sE


1
1
)()(
)(
)(
)(
sHsG
sG
sR
sC


1
0)()(1  sHsG
)(sG
)(sH
http://alltypeim.blogspot.in/

22. Example-4
R
_+
_
+1G 2G 3G
1H
2H
+
+
C
http://alltypeim.blogspot.in/

23. R
_+
_
+ 1G 2G 3G
1H
1
2
G
H
+
+
C
http://alltypeim.blogspot.in/

24. R
_+
_
+ 21GG 3G
1H
1
2
G
H
+
+
C
http://alltypeim.blogspot.in/

25. R
_+
_
+ 21GG 3G
1H
1
2
G
H
+
+
C
http://alltypeim.blogspot.in/

26. R
_+
_
+
121
21
1 HGG
GG
 3G
1
2
G
H
C
http://alltypeim.blogspot.in/

27. R
_+
_
+
121
321
1 HGG
GGG

1
2
G
H
C
http://alltypeim.blogspot.in/

28. R
_+
232121
321
1 HGGHGG
GGG

C
http://alltypeim.blogspot.in/

29. R
321232121
321
1 GGGHGGHGG
GGG

C
http://alltypeim.blogspot.in/

30. Example 5
Find the transfer function of the following block diagrams
2G 3G1G
4G
1H
2H
)(sY)(sR
http://alltypeim.blogspot.in/

31. 1. Moving pickoff point A ahead of block 2G
2. Eliminate loop I & simplify
324 GGG 
B
1G
2H
)(sY
4G
2G
1H
AB
3G
2G
)(sR
I
Solution:
http://alltypeim.blogspot.in/

32. 3. Moving pickoff point B behind block
324 GGG 
1G
B
)(sR
21GH 2H
)(sY
)/(1 324 GGG 
II
1G
B
)(sR C
324 GGG 
2H
)(sY
21GH
4G
2G A
3G 324 GGG 
http://alltypeim.blogspot.in/

33. 4. Eliminate loop III
)(sR
)(1
)(
3242121
3241
GGGHHGG
GGGG

 )(sY
)()(1
)(
)(
)(
)(
32413242121
3241
GGGGGGGHHGG
GGGG
sR
sY
sT



)(sR
1G
C
324
12
GGG
HG

)(sY
324 GGG 
2H
C
)(1 3242
324
GGGH
GGG


Using rule 6
http://alltypeim.blogspot.in/

34. ……THANK YOU……

http://alltypeim.blogspot.in/