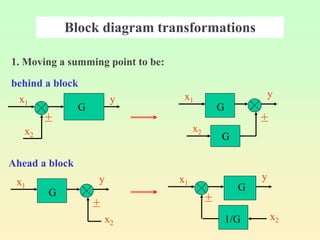
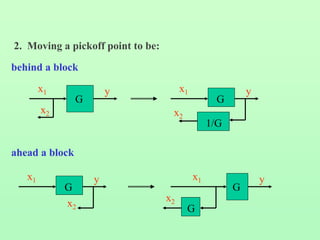
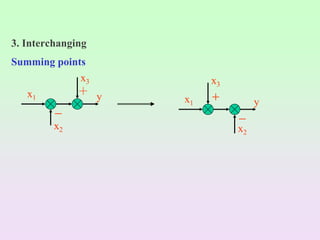
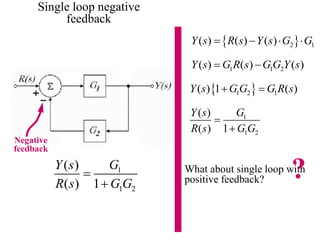
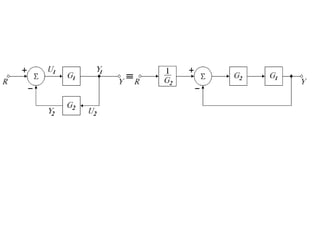
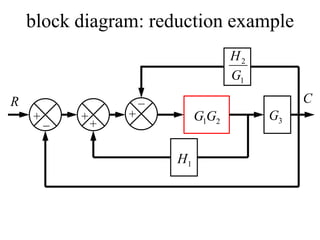
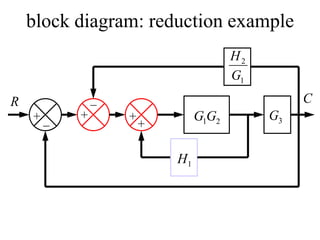
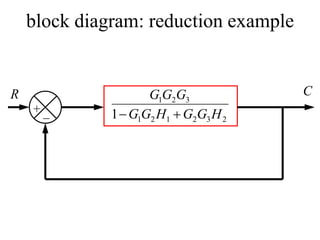
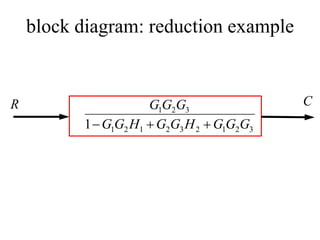
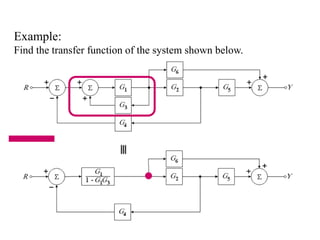
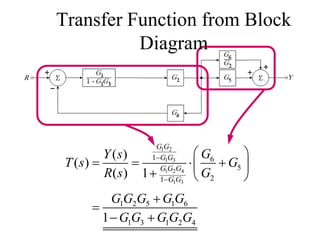
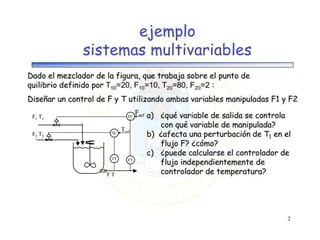
Block diagrams can be used to model systems and visualize mathematical relationships between components. They represent transfer functions of each component in boxes, with input-output connections shown by lines and arrows. Basic block diagram forms include cascade, parallel, and feedback configurations. Block diagrams can be simplified through algebraic transformations like moving summing or pickoff points. This allows determining the overall transfer function of a system from its block diagram representation.

1. Block Diagram Algebra

2. A graphical tool can help us to visualize the model of
a system and evaluate the mathematical
relationships between their elements, using their
transfer functions.
Using block diagram, we can solve the equations by
graphical simplification, which is often easier and
more informative than algebraic manipulation, even
though the methods are in every way equivalent
Introduction

3. Reminder: Component Block
Diagram

4. Block Diagram
• It represents the mathematical relationships between the
elements of the system.
• The transfer function of each component is placed in box,
and the input-output relationships between components
are indicated by lines and arrows.
)
(
)
(
)
( 1
1
1 s
Y
s
G
s
U 

5. Three basic forms
G1 G2
G2
G1
G1
G2
G1 G2 G1 G2 G1
G1
G2
1+
cascade parallel feedback

6. Block diagram transformations
behind a block
x1 y
G
±
x2
±
x1
x2
y
G
G
Ahead a block
±
x1
x2
y
G
x1
y
G
±
x2
1/G
1. Moving a summing point to be:

7. 2. Moving a pickoff point to be:
behind a block
G
x1
x2
y
G
x1
x2
y
1/G
ahead a block
G
x1
x2
y
G
G
x1
x2
y

8. 3. Interchanging
Summing points
x3
x1
x2
y
＋
－
x1
x3
y
＋
－
x2

9. Single loop negative
feedback
1
1 2
( )
( ) 1
G
Y s
R s G G


 
2 1
( ) ( ) ( )
Y s R s Y s G G
   
1 1 2
( ) ( ) ( )
Y s G R s GG Y s
 
 
1 2 1
( ) 1 ( )
Y s GG G R s
 
1
1 2
( )
( ) 1
G
Y s
R s G G


What about single loop with
positive feedback? ?
Negative
feedback

11. block diagram: reduction example
R
_
+
_
+ 1
G 2
G 3
G
1
H
1
2
G
H
+
+
C

12. block diagram: reduction example
R
_
+
_
+ 2
1G
G 3
G
1
H
1
2
G
H
+
+
C

13. block diagram: reduction example
R
_
+
_
+ 2
1G
G 3
G
1
H
1
2
G
H
+
+
C

14. block diagram: reduction example
R
_
+
_
+
1
2
1
2
1
1 H
G
G
G
G
 3
G
1
2
G
H
C

15. block diagram: reduction example
R
_
+
_
+
1
2
1
3
2
1
1 H
G
G
G
G
G

1
2
G
H
C

16. block diagram: reduction example
R
_
+
2
3
2
1
2
1
3
2
1
1 H
G
G
H
G
G
G
G
G


C

17. block diagram: reduction example
R
3
2
1
2
3
2
1
2
1
3
2
1
1 G
G
G
H
G
G
H
G
G
G
G
G



C

18. Example:
Find the transfer function of the system shown below.

19. 1 2 5 1 6
1 3 1 2 4
1
G G G G G
G G G G G


 
1 2
1 3
1 2 4
1 3
1 6
5
2
1
( )
( )
( ) 1
G G
G G
G G G
G G
G
Y s
T s G
R s G


 
   
 
  
Transfer Function from Block
Diagram

20. Example:
Find the transfer function of the system shown below.

21. 1 2 5 1 6
1 3 1 2 4
1
G G G G G
G G G G G


 
1 2
1 3
1 2 4
1 3
1 6
5
2
1
( )
( )
( ) 1
G G
G G
G G G
G G
G
Y s
T s G
R s G


 
   
 
  
Transfer Function from Block
Diagram

22. Moving pickoff point
G1 G2 G3 G4
H3
H2
H1
a b
G4
1
G1 G2
G3 G4
H3
H2
H1

23. ?
1 2
1 2
( )
( ) 1
R
Y s G G
R s G G H


When D(s)  0,
When R(s)  0,
2 2
1 2 1 2
( )
( ) 1 ( ) 1
D
Y s G G
D s G G H G G H
 
  
Example: MISO
Find the response of the system Y(s) to simultaneous application of
the reference input R(s) and disturbance D(s).

24. Example MISO
( ) ( ) ( )
R D
Y s Y s Y s
 
1 2 2
1 2 1 2
( ) ( ) ( )
1 1
G G G
Y s R s D s
G G H G G H
 
 
 
2
1
1 2
( ) ( ) ( )
1
G
Y s G R s D s
G G H
 
