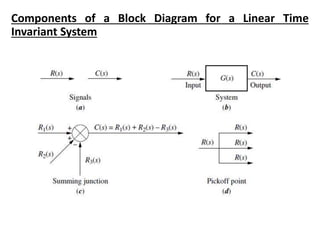
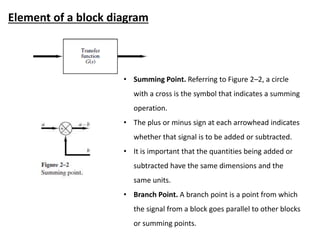
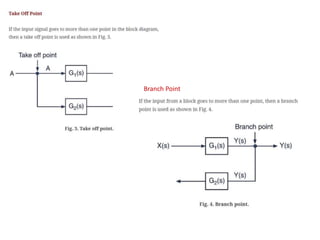
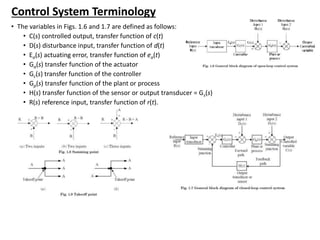
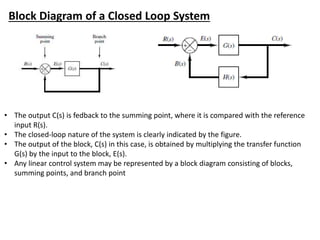
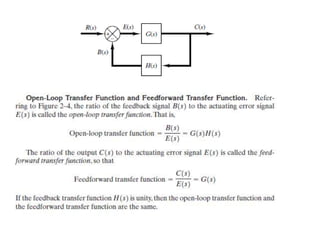
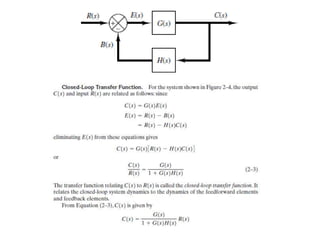
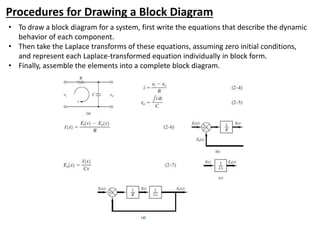
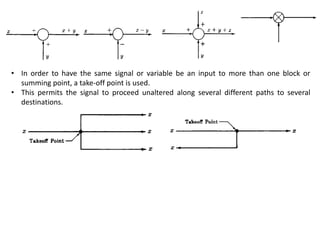
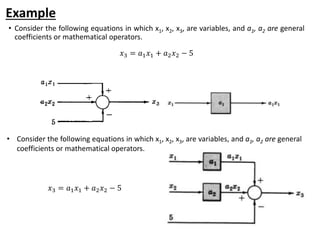
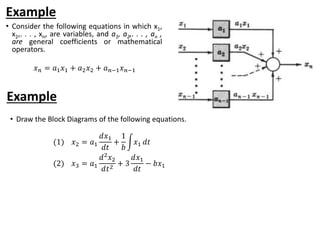
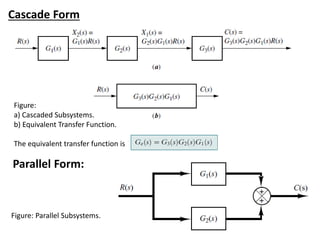
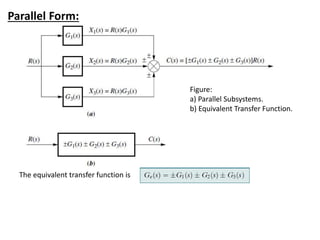
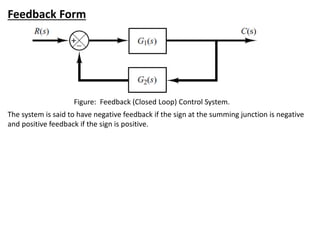
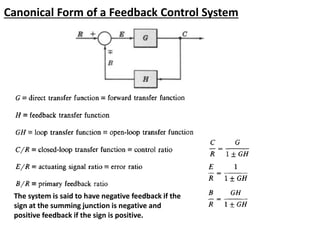
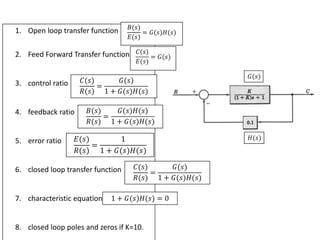
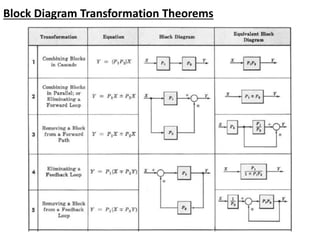
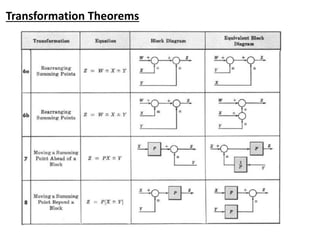
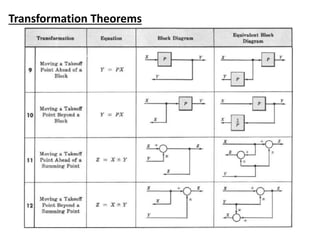
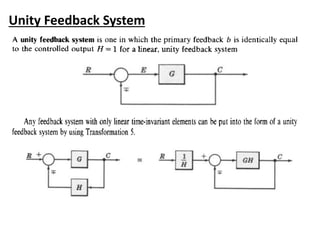
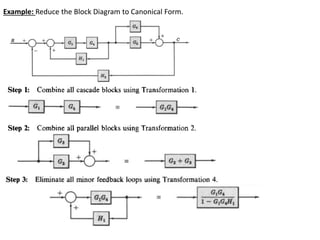
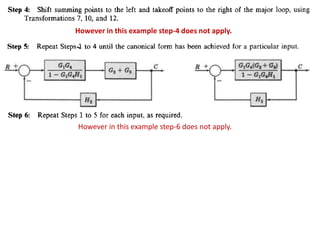
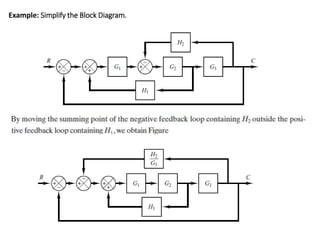
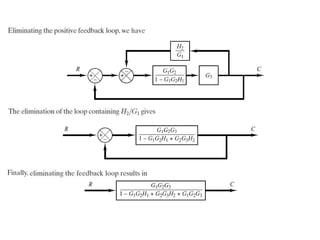
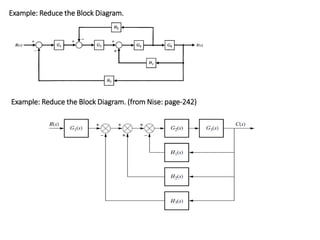
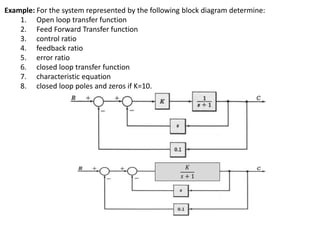
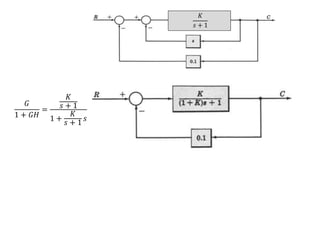
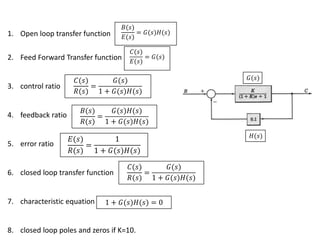
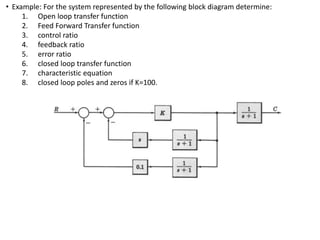
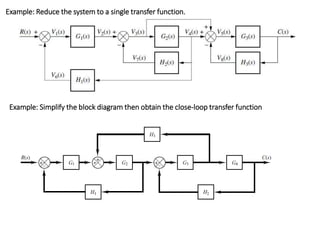
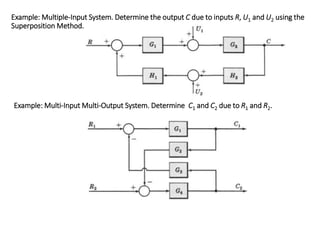
The document outlines the principles of biomedical control systems, focusing on block diagrams and their role in analyzing linear time-invariant systems. It describes key components such as transfer functions, summing points, branch points, and the significance of feedback in closed-loop systems. Additionally, it provides procedures for constructing block diagrams and examples to illustrate different configurations and transfer functions.

1. Biomedical Control Systems (BCS)
Block Diagram Reduction

2. Transfer Function
Transfer Function. The transfer function of a linear, time-invariant, differential equation
system is defined as the ratio of the Laplace transform of the output (response function) to
the Laplace transform of the input (driving function) under the assumption that all initial
conditions are zero.
Consider the linear time-invariant system defined by the following differential equation:

3. Introduction
• A Block Diagram is a shorthand pictorial representation of the cause-and-effect
relationship of a system.
• The interior of the rectangle representing the block usually contains a description of or
the name of the element, or the symbol for the mathematical operation to be performed
on the input to yield the output.
• The arrows represent the direction of information or signal flow.
𝑑
𝑑𝑡
𝑥 𝑦
• The operations of addition and subtraction have a special representation.
• The block becomes a small circle, called a summing point, with the appropriate plus or
minus sign associated with the arrows entering the circle.
• The output is the algebraic sum of the inputs.
• Any number of inputs may enter a summing point.
• Some books put a cross in the circle.

4. Components of a Block Diagram for a Linear Time
Invariant System

5. Element of a block diagram
• Summing Point. Referring to Figure 2–2, a circle
with a cross is the symbol that indicates a summing
operation.
• The plus or minus sign at each arrowhead indicates
whether that signal is to be added or subtracted.
• It is important that the quantities being added or
subtracted have the same dimensions and the
same units.
• Branch Point. A branch point is a point from which
the signal from a block goes parallel to other blocks
or summing points.

6. Branch Point

7. • The variables in Figs. 1.6 and 1.7 are defined as follows:
• C(s) controlled output, transfer function of c(t)
• D(s) disturbance input, transfer function of d(t)
• Ea(s) actuating error, transfer function of ea(t)
• Ga(s) transfer function of the actuator
• Gc(s) transfer function of the controller
• Gp(s) transfer function of the plant or process
• H(s) transfer function of the sensor or output transducer = Gs(s)
• R(s) reference input, transfer function of r(t).
Control System Terminology

8. Block Diagram of a Closed Loop System
• The output C(s) is fedback to the summing point, where it is compared with the reference
input R(s).
• The closed-loop nature of the system is clearly indicated by the figure.
• The output of the block, C(s) in this case, is obtained by multiplying the transfer function
G(s) by the input to the block, E(s).
• Any linear control system may be represented by a block diagram consisting of blocks,
summing points, and branch point

11. Closed-Loop System Subjected to a Disturbance
• Figure 2–11 shows a closed loop system subjected to a disturbance.
• When two inputs (the reference input and disturbance) are present in a linear time-
invariant system, each input can be treated independently of the other; and the
outputs corresponding to each input alone can be added to give the complete
output.
• The way each input is introduced into the system is shown at the summing point by
either a plus or minus sign.

12. Procedures for Drawing a Block Diagram
• To draw a block diagram for a system, first write the equations that describe the dynamic
behavior of each component.
• Then take the Laplace transforms of these equations, assuming zero initial conditions,
and represent each Laplace-transformed equation individually in block form.
• Finally, assemble the elements into a complete block diagram.

13. • In order to have the same signal or variable be an input to more than one block or
summing point, a take-off point is used.
• This permits the signal to proceed unaltered along several different paths to several
destinations.

14. Example
• Consider the following equations in which x1, x2, x3, are variables, and a1, a2 are general
coefficients or mathematical operators.
𝑥3 = 𝑎1𝑥1 + 𝑎2𝑥2 − 5
• Consider the following equations in which x1, x2, x3, are variables, and a1, a2 are general
coefficients or mathematical operators.
𝑥3 = 𝑎1𝑥1 + 𝑎2𝑥2 − 5

15. Example
• Consider the following equations in which x1,
x2,. . . , xn, are variables, and a1, a2,. . . , an ,
are general coefficients or mathematical
operators.
𝑥𝑛 = 𝑎1𝑥1 + 𝑎2𝑥2 + 𝑎𝑛−1𝑥𝑛−1
Example
• Draw the Block Diagrams of the following equations.
(1) 𝑥2 = 𝑎1
𝑑𝑥1
𝑑𝑡
+
1
𝑏
𝑥1 𝑑𝑡
(2) 𝑥3 = 𝑎1
𝑑2𝑥2
𝑑𝑡2 + 3
𝑑𝑥1
𝑑𝑡
− 𝑏𝑥1

16. Cascade Form
Figure:
a) Cascaded Subsystems.
b) Equivalent Transfer Function.
The equivalent transfer function is
Parallel Form:
Figure: Parallel Subsystems.

17. Parallel Form:
Figure:
a) Parallel Subsystems.
b) Equivalent Transfer Function.
The equivalent transfer function is

18. Feedback Form
Figure: Feedback (Closed Loop) Control System.
The system is said to have negative feedback if the sign at the summing junction is negative
and positive feedback if the sign is positive.

19. Characteristic Equation

20. Canonical Form of a Feedback Control System
The system is said to have negative feedback if the
sign at the summing junction is negative and
positive feedback if the sign is positive.

22. 1. Open loop transfer function
2. Feed Forward Transfer function
3. control ratio
4. feedback ratio
5. error ratio
6. closed loop transfer function
7. characteristic equation
8. closed loop poles and zeros if K=10.
𝐵(𝑠)
𝐸(𝑠)
= 𝐺(𝑠)𝐻(𝑠)
𝐶(𝑠)
𝐸(𝑠)
= 𝐺(𝑠)
𝐶(𝑠)
𝑅(𝑠)
=
𝐺(𝑠)
1 + 𝐺(𝑠)𝐻(𝑠)
𝐵(𝑠)
𝑅(𝑠)
=
𝐺(𝑠)𝐻(𝑠)
1 + 𝐺(𝑠)𝐻(𝑠)
𝐸(𝑠)
𝑅(𝑠)
=
1
1 + 𝐺(𝑠)𝐻(𝑠)
𝐶(𝑠)
𝑅(𝑠)
=
𝐺(𝑠)
1 + 𝐺(𝑠)𝐻(𝑠)
1 + 𝐺(𝑠)𝐻(𝑠) = 0
𝐺(𝑠)
𝐻(𝑠)

23. Block Diagram Transformation Theorems

24. Transformation Theorems

25. Transformation Theorems

26. Unity Feedback System

27. Reduction of Complicated Block Diagrams:

28. Example: Reduce the Block Diagram to Canonical Form.

29. However in this example step-4 does not apply.
However in this example step-6 does not apply.

30. Example: Simplify the Block Diagram.

32. Example: Reduce the Block Diagram.
Example: Reduce the Block Diagram. (from Nise: page-242)

33. Example: For the system represented by the following block diagram determine:
1. Open loop transfer function
2. Feed Forward Transfer function
3. control ratio
4. feedback ratio
5. error ratio
6. closed loop transfer function
7. characteristic equation
8. closed loop poles and zeros if K=10.
𝐾
𝑠 + 1

34. 𝐾
𝑠 + 1
𝐺
1 + 𝐺𝐻
=
𝐾
𝑠 + 1
1 +
𝐾
𝑠 + 1
𝑠

35. 1. Open loop transfer function
2. Feed Forward Transfer function
3. control ratio
4. feedback ratio
5. error ratio
6. closed loop transfer function
7. characteristic equation
8. closed loop poles and zeros if K=10.
𝐵(𝑠)
𝐸(𝑠)
= 𝐺(𝑠)𝐻(𝑠)
𝐶(𝑠)
𝐸(𝑠)
= 𝐺(𝑠)
𝐶(𝑠)
𝑅(𝑠)
=
𝐺(𝑠)
1 + 𝐺(𝑠)𝐻(𝑠)
𝐵(𝑠)
𝑅(𝑠)
=
𝐺(𝑠)𝐻(𝑠)
1 + 𝐺(𝑠)𝐻(𝑠)
𝐸(𝑠)
𝑅(𝑠)
=
1
1 + 𝐺(𝑠)𝐻(𝑠)
𝐶(𝑠)
𝑅(𝑠)
=
𝐺(𝑠)
1 + 𝐺(𝑠)𝐻(𝑠)
1 + 𝐺(𝑠)𝐻(𝑠) = 0
𝐺(𝑠)
𝐻(𝑠)

36. • Example: For the system represented by the following block diagram determine:
1. Open loop transfer function
2. Feed Forward Transfer function
3. control ratio
4. feedback ratio
5. error ratio
6. closed loop transfer function
7. characteristic equation
8. closed loop poles and zeros if K=100.

37. Example: Reduce the system to a single transfer function.
Example: Simplify the block diagram then obtain the close-loop transfer function

38. Example: Multiple-Input System. Determine the output C due to inputs R, U1 and U2 using the
Superposition Method.
Example: Multi-Input Multi-Output System. Determine C1 and C2 due to R1 and R2.