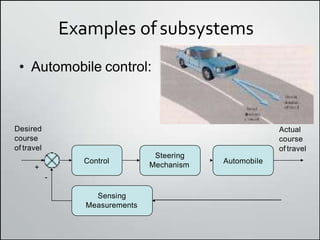
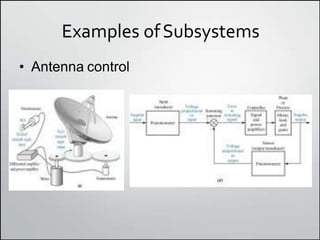
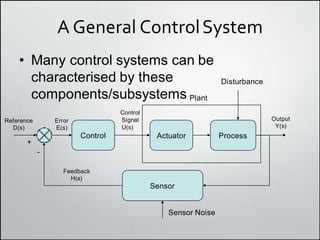
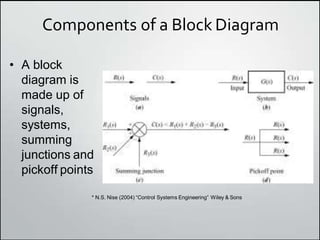
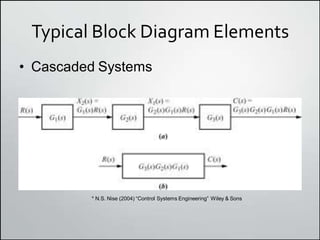
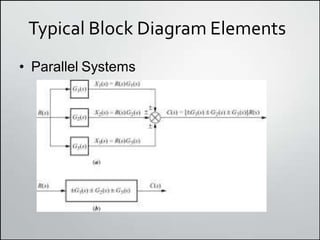
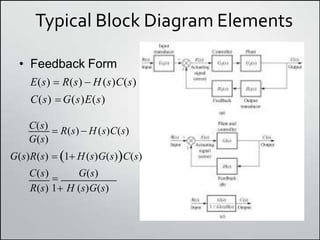
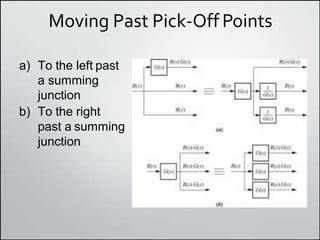
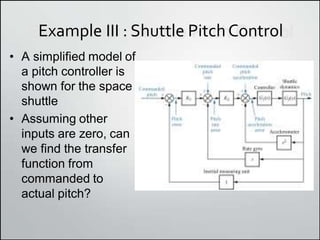
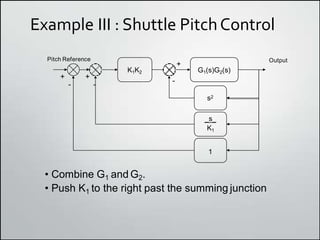
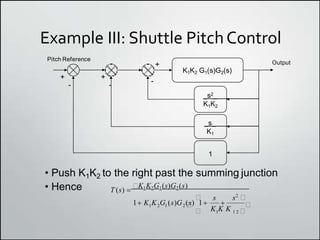
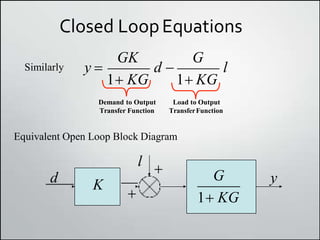
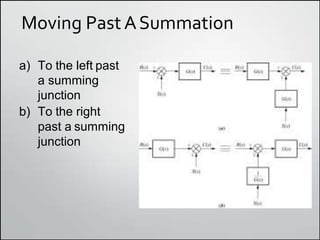
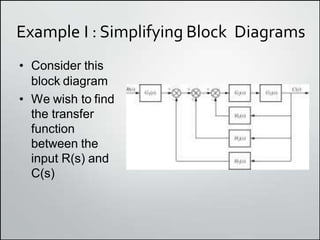
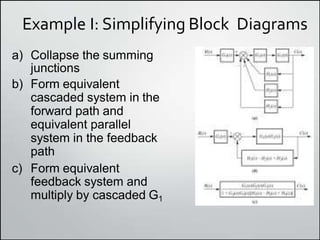
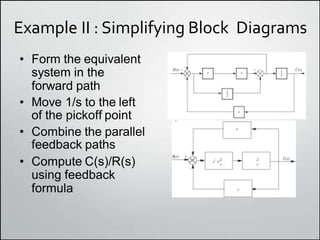
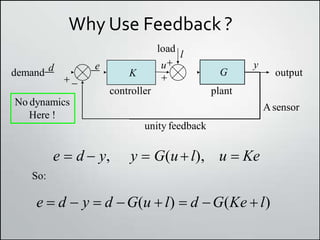
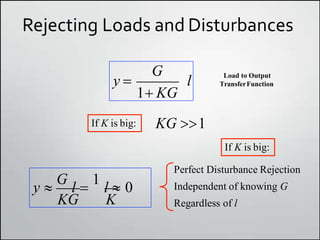
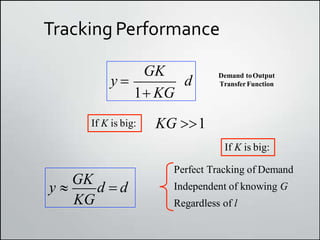
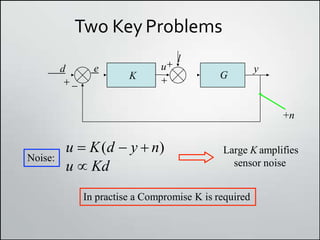
1. Block diagrams can be used to represent subsystems in a system using inputs, outputs, and transfer functions. Multiple subsystems can be combined using rules for cascaded, parallel, and feedback systems. 2. Simplifying block diagrams allows us to find the overall system transfer function by reducing the diagram to an equivalent form. Examples show how to simplify complex diagrams. 3. Feedback control is useful for rejecting disturbances and improving tracking performance, but large feedback gains can amplify sensor noise, so a compromise is needed.

1. Block Diagrams Algebra
Presentation
Submitted By :
Name : Tushar Devaji Khodankar
Enrollment No. : BE18S02F010
Course Code : ME 4017
Course Name : Automatic Control System
Branch/Year : Mechanical (BE)

2. BlockDiagrams
• As we saw in the introductory lecture, a
subsystem can be represented with an
input, an output and a transfer function
U(s) Y(s)
H(s)
Input: control surfaces
(flap, aileron), wind gust
Aircraft output: pitch, yaw, roll

3. Block Diagrams
• Many systems are composed of multiple
subsystems
• In this lecture we will examine methods for
combining subsystems and simplifying
block diagrams

4. Examples of subsystems
• Automobile control:
Sensing
Measurements
Steering
Mechanism
Automobile
Control
Desired
course
of travel
Actual
course
of travel
-
+

5. Examples ofSubsystems
• Antenna control

6. Mathematical Modelling
h(t)
• In the time domain, the input-output relationship is
usually expressed in terms of a differential equation
u(t) y(t)
• (an-1, …, a0, bm, … b0) are the systemʼs parameters, n ≥
m
• The system is LTI (Linear Time Invariant) iff the
parameters are time-invariant
• n is the order of the system
dtn
dtm
an1
dtn1
dn
y(t)  dn1
y(t) dm
u(t)
L  a0 y(t) bm L b0u(t)

7. Mathematical Modelling
H(s)
• In the Laplace domain, the input-output relationship is
usually expressed in terms of an algebraic equation in
terms of s
U(s) Y(s)
m 0
n1 m
n1 0
sn
Y(s)  a s Y(s) L  a Y(s)  b s U(s) L b U(s)

8. Cascaded systems
• In time, a cascaded
system requires a
convolution
• In the Laplace
domain, this is simply
a product
H(s)
U(s) Y1(s)
H1(s)
Y(s)
Y(s) U(s)H(s)H1(s)
htd



h(t)
utht u
u(t) y1(t)
h1(t)
y(t)
y(t) (u(t)*h(t))*h1(t)

9. A General ControlSystem
• Many control systems can be
Sensor
Actuator Process
Control
Reference
D(s)
Output
Y(s)
+
Error
E(s)
Control
Signal
U(s)
characterised by these
components/subsystems Plant
Disturbance
Sensor Noise
-
Feedback
H(s)

10. Simplifying Block Diagrams
• The objectives of a block diagram are
– To provide an understanding of the signal
flows in the system
– To enable modelling of complex systems from
simple building blocks
– To allow us to generate the overall system
transfer function
• A few rules allow us to simplify complex
block diagrams into familiar forms

11. Components of a Block Diagram
• A block
diagram is
made up of
signals,
systems,
summing
junctions and
pickoff points
* N.S. Nise (2004) “Control Systems Engineering” Wiley & Sons

12. Typical Block Diagram Elements
• Cascaded Systems
* N.S. Nise (2004) “Control Systems Engineering” Wiley & Sons

13. Typical Block Diagram Elements
• Parallel Systems

14. Typical Block Diagram Elements
• Feedback Form
E(s)  R(s)  H (s)C(s)
C(s) G(s)E(s)
C(s)
 R(s)  H(s)C(s)
G(s)
G(s)R(s)  1 H(s)G(s)C(s)
C(s)  G(s)
R(s) 1 H (s)G(s)

15. Moving Past ASummation
a) To the left past
a summing
junction
b) To the right
past a summing
junction

16. Moving Past Pick-Off Points
a) To the left past
a summing
junction
b) To the right
past a summing
junction

17. Example I : Simplifying Block Diagrams
• Consider this
block diagram
• We wish to find
the transfer
function
between the
input R(s) and
C(s)

18. Example I: Simplifying Block Diagrams
a) Collapse the summing
junctions
b) Form equivalent
cascaded system in the
forward path and
equivalent parallel
system in the feedback
path
c) Form equivalent
feedback system and
multiply by cascaded G1

19. Example II : Simplifying Block Diagrams
• Form the equivalent
system in the
forward path
• Move 1/s to the left
of the pickoff point
• Combine the parallel
feedback paths
• Compute C(s)/R(s)
using feedback
formula

20. Example III: Shuttle PitchControl
• Manipulating block
diagrams is important
but how do they relate
to the real world?
• Here is an example of
a real system that
incorporates feedback
to control the pitch of
the vehicle (amongst
other things)

21. Example III: Shuttle PitchControl
• The control
mechanisms
available include
the body flap,
elevons and
engines
• Measurements
are made by the
vehicleʼs inertial
unit, gyros and
accelerometers * N.S. Nise (2004) “Control Systems Engineering” Wiley & Sons

22. Example III : Shuttle PitchControl
• A simplified model of
a pitch controller is
shown for the space
shuttle
• Assuming other
inputs are zero, can
we find the transfer
function from
commanded to
actual pitch?

23. Example III : Shuttle PitchControl
G1(s)G2(s)
K1K2
Pitch Reference Output
-
+
- -
+ +
_s_
K1
1
s2
• Combine G1 and G2.
• Push K1 to the right past the summing junction

24. Example III: Shuttle PitchControl
K1K2 G1(s)G2(s)
Pitch Reference
Output
-
+
-
+
-
+
_s2_
K1K2
_s_
K1
1
• Push K1K2 to the right past the summing junction
• Hence
K K K
T (s) 
K1K2G1(s)G2(s)
 s s2

1 K K G (s)G (s) 1 
1 2 1 2  
 1 1 2 

25. Example III: Shuttle PitchControl
• Matlab provides us with a tool called
Simulink that allows us to represent
systems by their block diagram
• Weʼll take a bit of time to see how we
construct a Simulink model of this system

26. Closed LoopFeedback
• We have suggested that many control
systems take on a familiar feedback form
• Intuition tells us that feedback is useful –
imagine driving your car with your eyes
closed
• Let us examine why this is the case from a
mathematical perspective

27. Single-Loop FeedbackSystem
Value
Output
Transducer
Desired+
-
Feedback
Signal
Controller Plant
Control
Signal
K(s) G(s)
H
d(t) e(t) u(t)
error
y(t)
f (t)
• Error Signal e(t)  d(t)  f (t)  d(t)  Ky(t)
• The goal of the Controller K(s) is:


To produce a control signal u(t) that
drives the ʻerrorʼ e(t) to zero

28. ControllerObjectives
• Controller cannot drive error to zero
instantaneously as the plant G(s) has dynamics
• Clearly a ʻlargeʼ control signal will move the
plant more quickly
• The gain of the controller should be large so that
even small values of e(t) will produce large
values of u(t)
• However, large values of gain will cause
instability

29. Feedforward &Feedback
• Driving a Formula-1 car
• Feedforward control: pre-emptive/predictable
action: prediction of carʼs direction of travel
(assuming the model is accurate enough)
• Feeback control: corrective action since the
model is not perfect + noise

30. Why Use Feedback ?
• Perfect feed-forward controller: Gn
• Output and error: Gn
y 
G
d  Gl
 G 
e  d  y  1
G 
d  Gl
• Only zero when:
Gn  G
 n 
(Perfect Knowledge)
l  0 (No load or disturbance)
y(t)
d(t)
1/Gn
l(t)


G

31. Why Use Feedback ?
e

 
K
u
unity feedback
G
y
controller plant
demand d output
Asensor
load
l
No dynamics
Here !
e  d  y, y  G(ul), u  Ke
So:
e  d  y  d G(u  l)  d G(Ke  l)

32. Closed LoopEquations
e  d GKeGl
1KGe  d Gl
Collect terms:
1 G
e  d  l
1 KG 1 KG
Or:
Demand to Error Load to Error
Transfer Function TransferFunction

33. Closed LoopEquations
G
1 KG
K
d
l
y


Equivalent Open Loop Block Diagram
GK G
y  d  l
1 KG 1 KG
Similarly
Demand to Output Load to Output
Transfer Function TransferFunction

34. Rejecting Loads and Disturbances
l
y 
G
1 KG
Load to Output
TransferFunction
If K is big: KG 1
KG K
y 
G
l 
1
l  0
If K is big:
Perfect Disturbance Rejection
Independent of knowing G
Regardless of l

35. Tracking Performance
d
y 
GK
1 KG
Demand toOutput
TransferFunction
If K is big: KG 1
KG
y 
GK
d  d
If K is big:
Perfect Tracking of Demand
Independent of knowing G
Regardless of l

36. Two Key Problems
y

d e
 
u l
K G
Noise:
Large K amplifies
sensor noise
u  K(d  y  n)
u  Kd
In practise a Compromise K is required
+n

37. Conclusions
• We have examined methods for
computing the transfer function by
reducing block diagrams to simple form
• We have also presented arguments for
using feedback in control systems