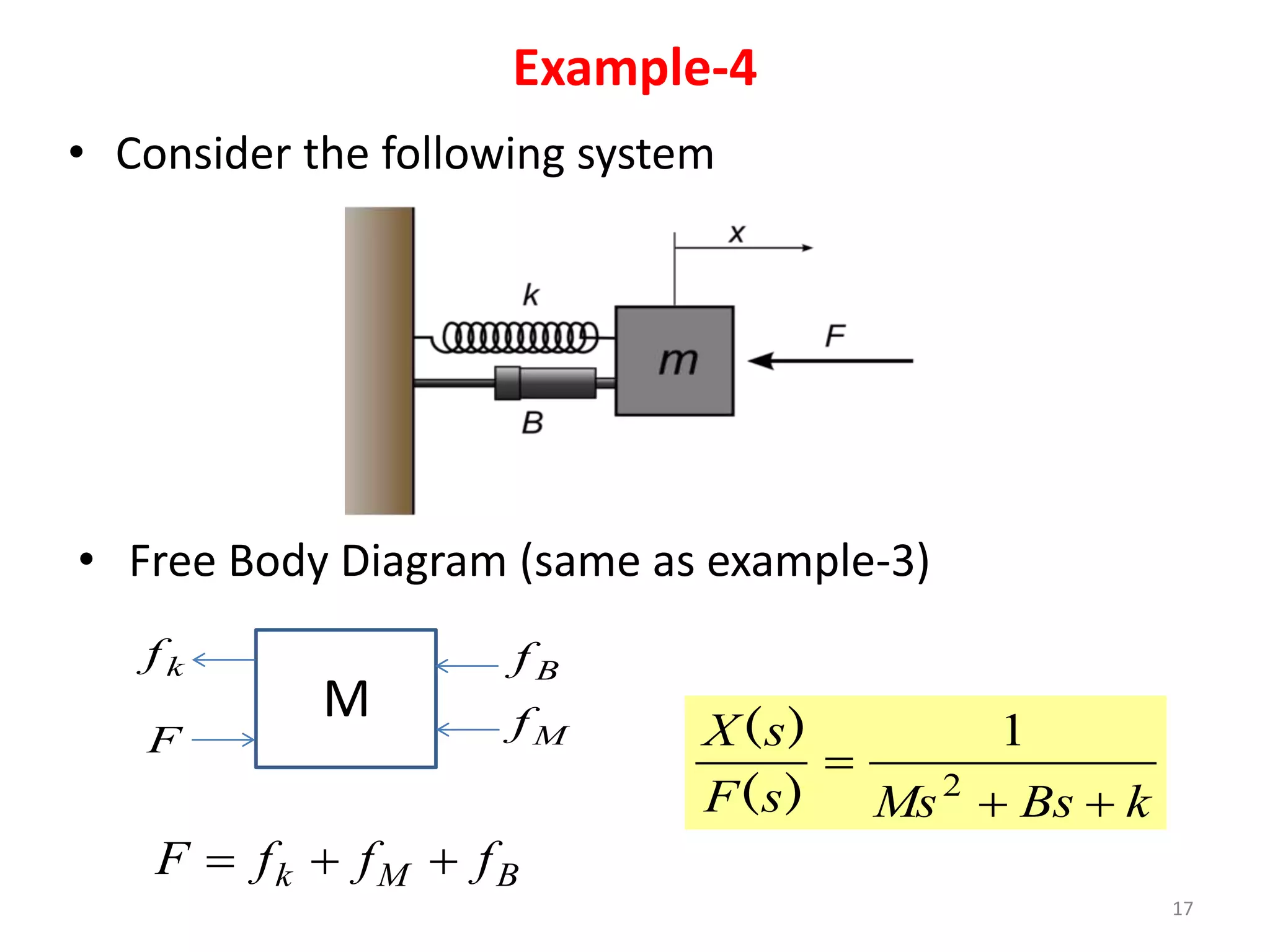
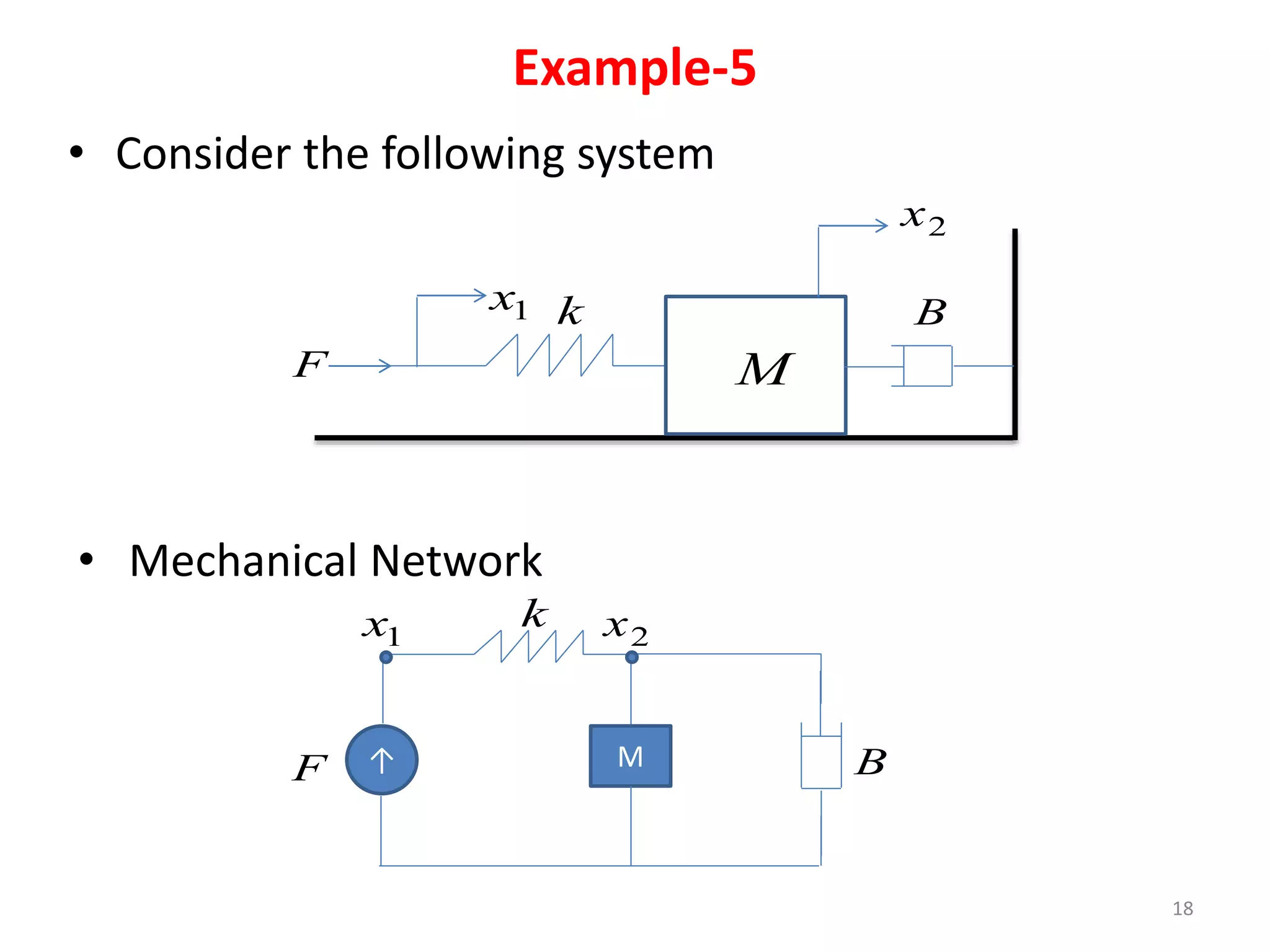
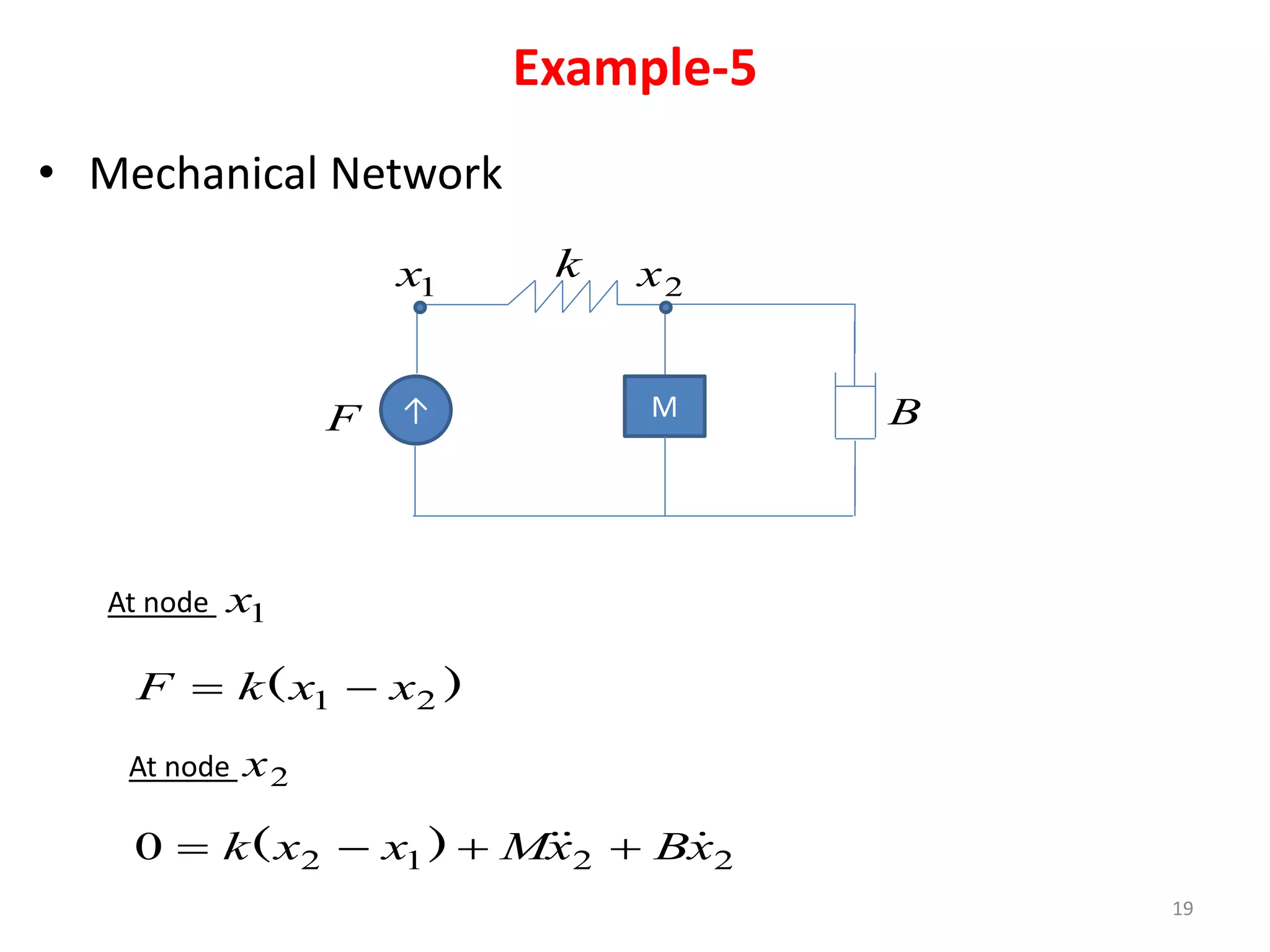
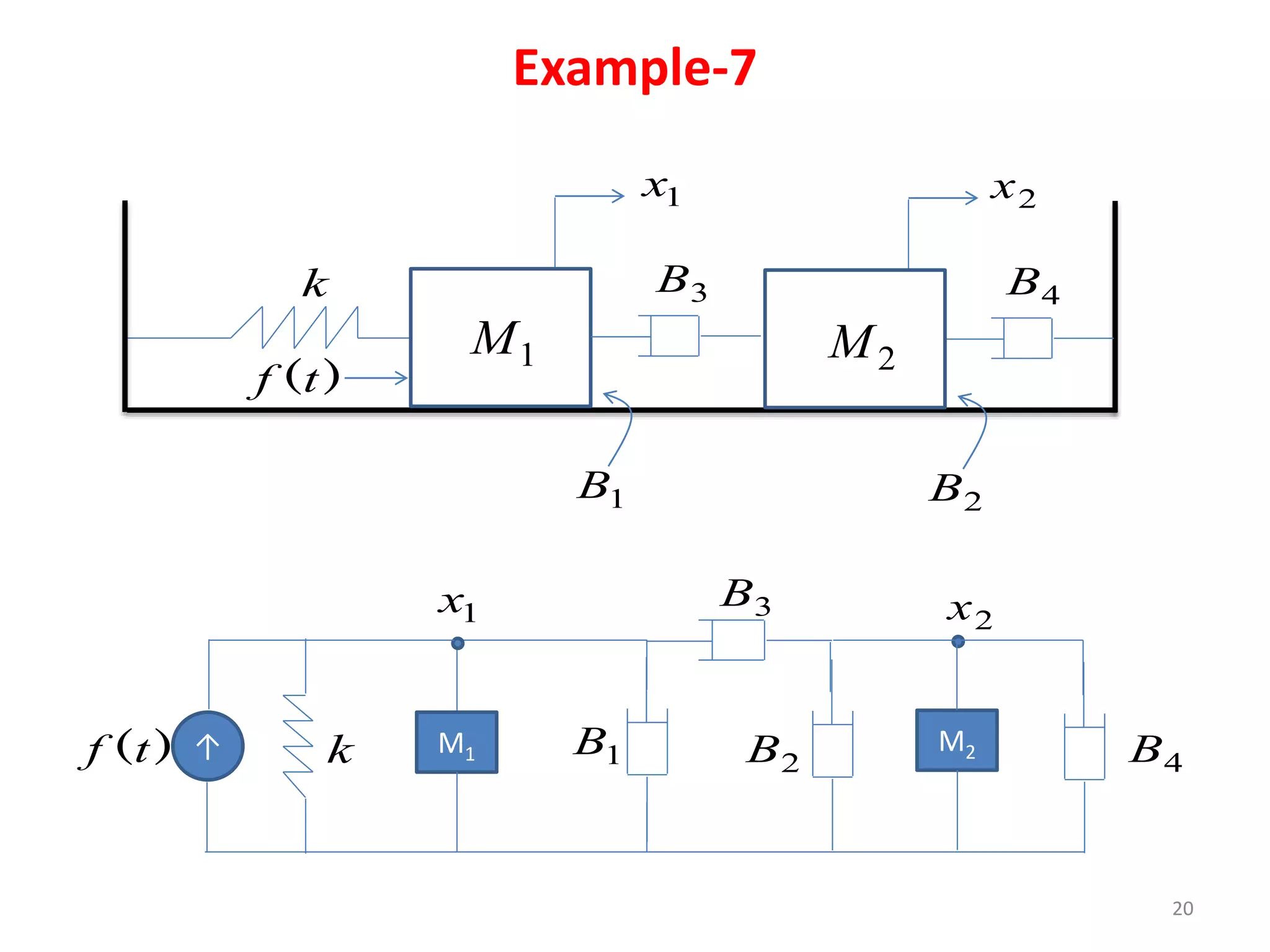
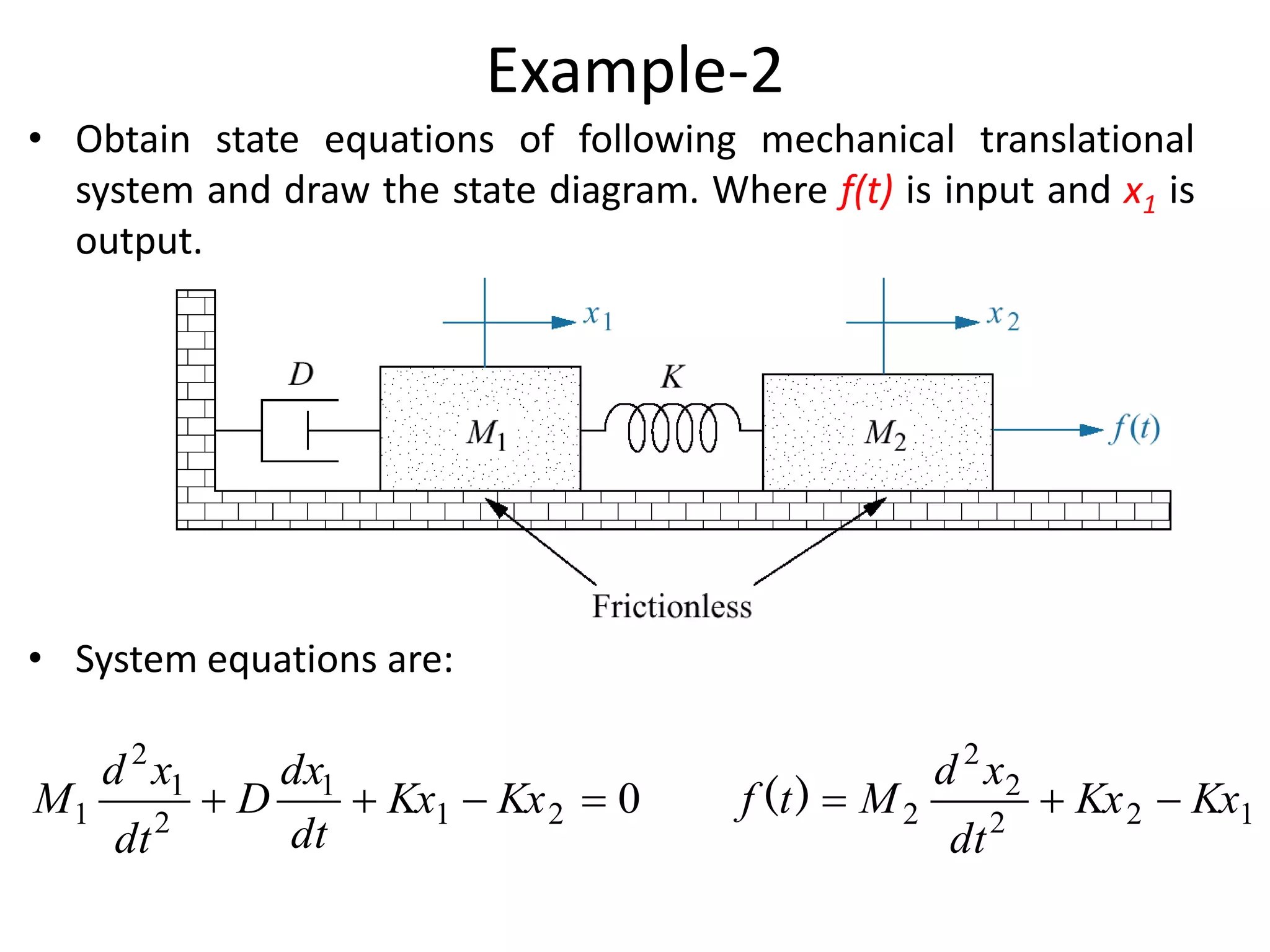
This document summarizes modeling of mechanical translational systems. It discusses modeling basic elements like springs, masses, and dampers and provides their equations of motion. Examples are given of modeling multiple springs, masses and dampers connected together in different configurations. The state equations and state diagram are obtained for a sample mechanical translational system with multiple springs and dampers connecting different masses.

1. Modeling of Mechanical System-
Translational
•Basic Elements Modeling-Spring(K),
Damper(D), Mass(M)
•Solved Examples with KDM
1

2. Basic motion concepts
v  adt ;
x  vdt ;
dt
f 
d
mv  ma N
dt
T 
d
J  J Nm
J , Moment of inertia
For rotational systems
 dt ;    dt
For translational systems
2
..

3. Basic Elements of Translational Mechanical Systems
Translational Spring
i)
Translational Mass
ii)
Translational Damper
iii)

4. Translational Spring
i)
Circuit Symbols
Translational Spring
• A translational spring is a mechanical element that
can be deformed by an external force such that the
deformation is directly proportional to the force
applied to it.
Translational Spring

5. Translational Spring
• If F is the applied force
• Then is the deformation if
• Or is the deformation.
• The equation of motion is given as
• Where is stiffness of spring expressed in N/m
2
x
1
x
0
2 
x
1
x
)
( 2
1 x
x 
)
( 2
1 x
x
k
F 

k
F
F

6. Translational Spring
• Given two springs with spring constant k1 and k2, obtain
the equivalent spring constant keq for the two springs
connected in:
6
(1) Parallel (2) Series

7. Translational Spring
7
(1) Parallel
F
x
k
x
k 
 2
1
F
x
k
k 
 )
( 2
1
F
x
keq 
• The two springs have same displacement therefore:
2
1 k
k
keq 

• If n springs are connected in parallel then:
n
eq k
k
k
k 


 
2
1

8. Translational Spring
8
(2) Series
F
x
k
x
k 
 2
2
1
1
• The forces on two springs are same, F, however
displacements are different therefore:
1
1
k
F
x 
2
2
k
F
x 
• Since the total displacement is , and we have
2
1 x
x
x 
 x
k
F eq

2
1
2
1
k
F
k
F
k
F
x
x
x
eq






9. Translational Spring
9
• Then we can obtain
2
1
2
1
2
1
1
1
1
k
k
k
k
k
k
keq




2
1 k
F
k
F
k
F
eq


• If n springs are connected in series then:
n
n
eq
k
k
k
k
k
k
k






2
1
2
1

10. Translational Mass
Translational Mass
ii)
• Translational Mass is an inertia
element.
• A mechanical system without
mass does not exist.
• If a force F is applied to a mass
and it is displaced to x meters
then the relation b/w force and
displacements is given by
Newton’s law.
M
)
(t
F
)
(t
x
x
M
F 



11. Translational Damper
Translational Damper
iii)
• When the viscosity or drag is not
negligible in a system, we often
model them with the damping
force.
• All the materials exhibit the
property of damping to some
extent.
• If damping in the system is not
enough then extra elements (e.g.
Dashpot) are added to increase
damping.

12. Translational Damper
x
C
F 

• Where C is damping coefficient (N/ms-1).
)
( 2
1 x
x
C
F 
 


13. Translational Damper
• Translational Dampers in series and parallel.
2
1 C
C
Ceq 

2
1
2
1
C
C
C
C
Ceq



14. Mechanical Translational
14

15. Example-3
• Consider the following system
15
• Free Body Diagram
k
F
x
M
C
M
F
k
f
M
f
C
f
C
M
k f
f
f
F 



16. Example-3
16
Differential equation of the system is:
kx
x
C
x
M
F 

 


Taking the Laplace Transform of both sides and ignoring
Initial conditions we get
)
(
)
(
)
(
)
( s
kX
s
CsX
s
X
Ms
s
F 

 2
k
Cs
Ms
s
F
s
X


 2
1
)
(
)
(

17. Example-4
• Consider the following system
17
• Free Body Diagram (same as example-3)
M
F
k
f
M
f
B
f
B
M
k f
f
f
F 


k
Bs
Ms
s
F
s
X


 2
1
)
(
)
(

18. Example-5
• Consider the following system
18
• Mechanical Network
k
F
2
x
M
1
x B
↑ M
k
B
F
1
x 2
x

19. Example-5
19
• Mechanical Network
↑ M
k
B
F
1
x 2
x
)
( 2
1 x
x
k
F 

At node 1
x
At node 2
x
2
2
1
2
0 x
B
x
M
x
x
k 

 


 )
(

20. Example-7
20
k
)
(t
f
2
x
1
M
4
B
3
B
2
M
1
x
1
B 2
B
↑ M1
k 1
B
)
(t
f
1
x 2
x
3
B
2
B M2
4
B

21. Example-2
• Obtain state equations of following mechanical translational
system and draw the state diagram. Where f(t) is input and x1 is
output.
0
2
1
1
2
1
2
1 


 Kx
Kx
dt
dx
D
dt
x
d
M 1
2
2
2
2
2 Kx
Kx
dt
x
d
M
t
f 


)
(
• System equations are:

22. Translational mechanical
system transfer functions
M1s2 + ( fv1 + fv3 )s +(K1 + K2) X1(s) −( fv3 s+ K2)X2(s) = F(s)

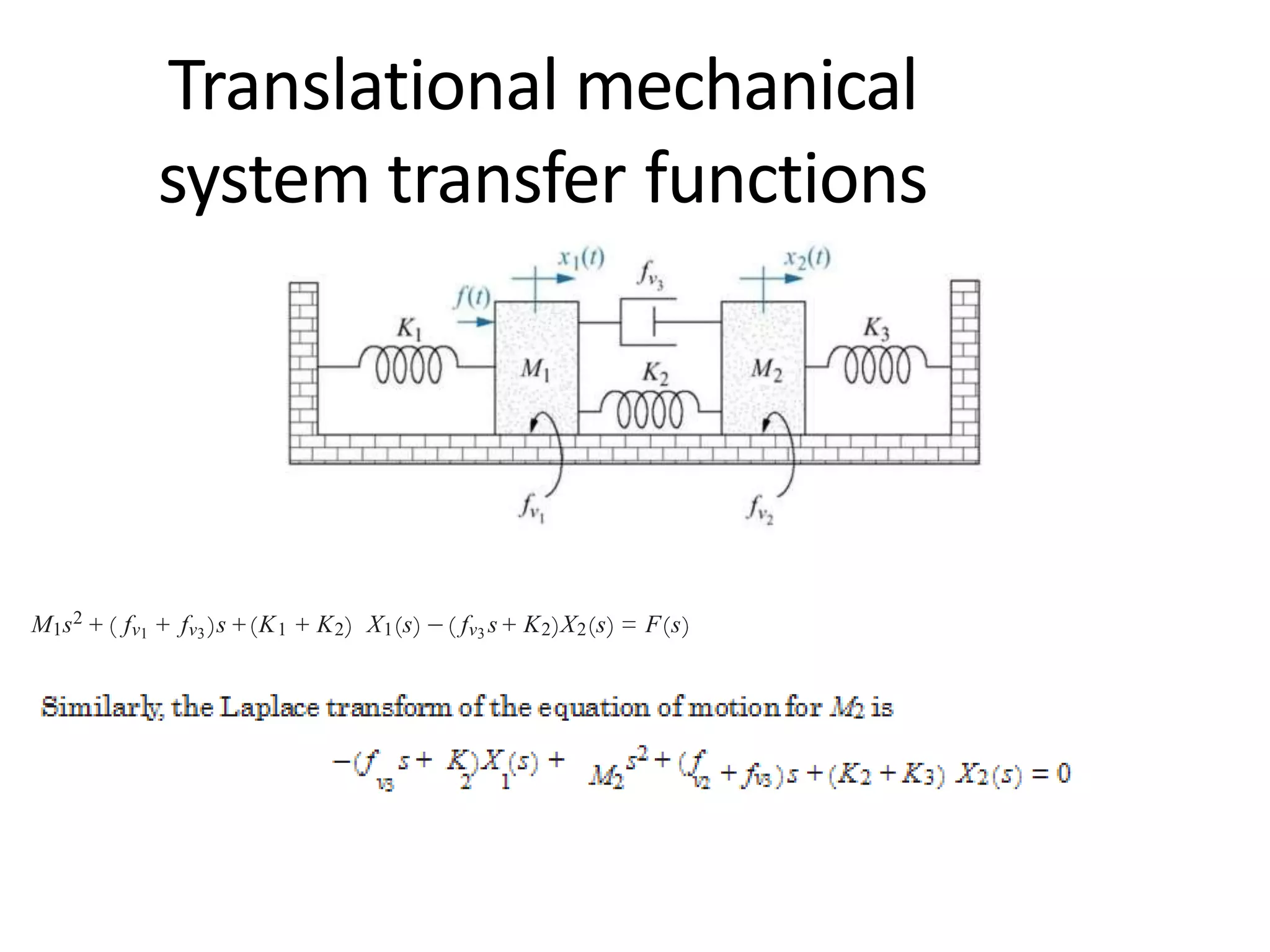
23. Solution (Cont’d) M1 has two springs, two viscous dampers, and mass associated with its motion.
There is one spring between M1 and M2, and one viscous damper between M1 and M3. Thus, the
equation of motion for M1 is
[M1s2 + ( fv1 + fv3 )s +(K1 + K2)]X1(s) −K2X2(s) − fv3 sX3(s) = 0
Similarly, the equations of motion for M2 and M3 are
−K2X1(s)+[M2s2 + ( fv2 + fv4 )s + K2]X2(s) − fv4 sX3(s) = F(s)
−fv3 sX1(s) − fv4 sX2(s) +[M3s2 + ( fv3 + fv4 )s]X3(s) = 0
.

24. 24

25. 25