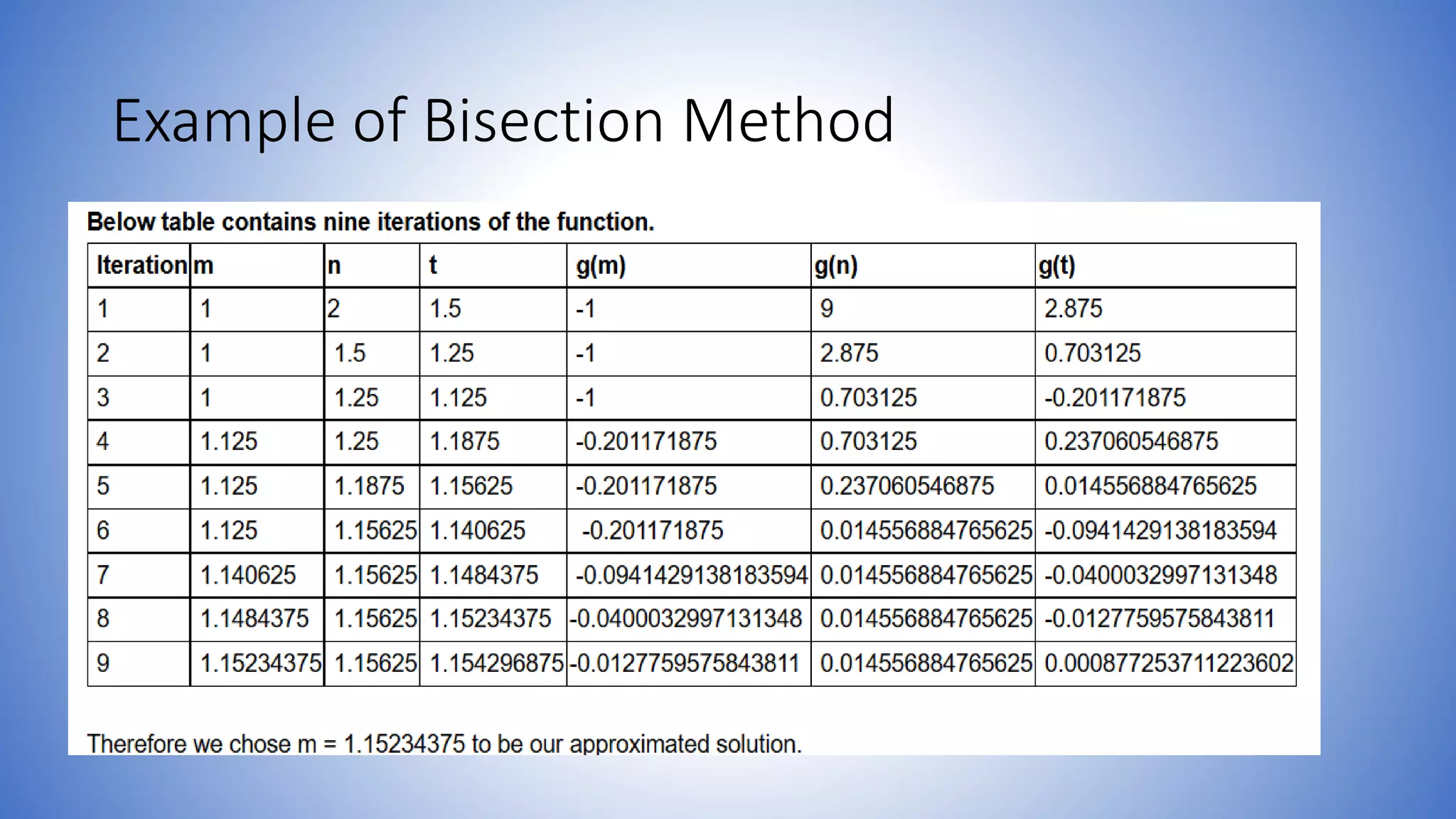
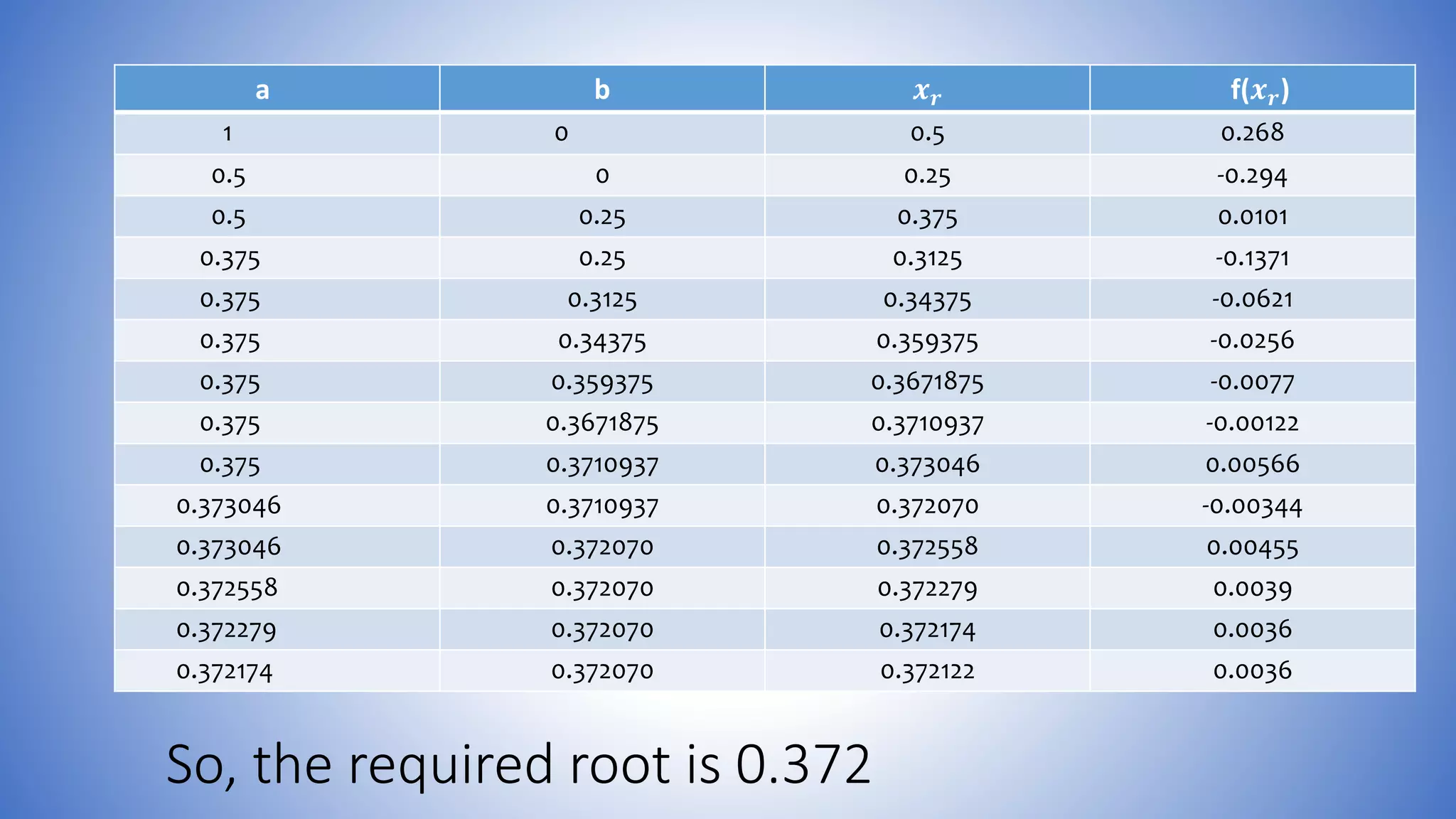
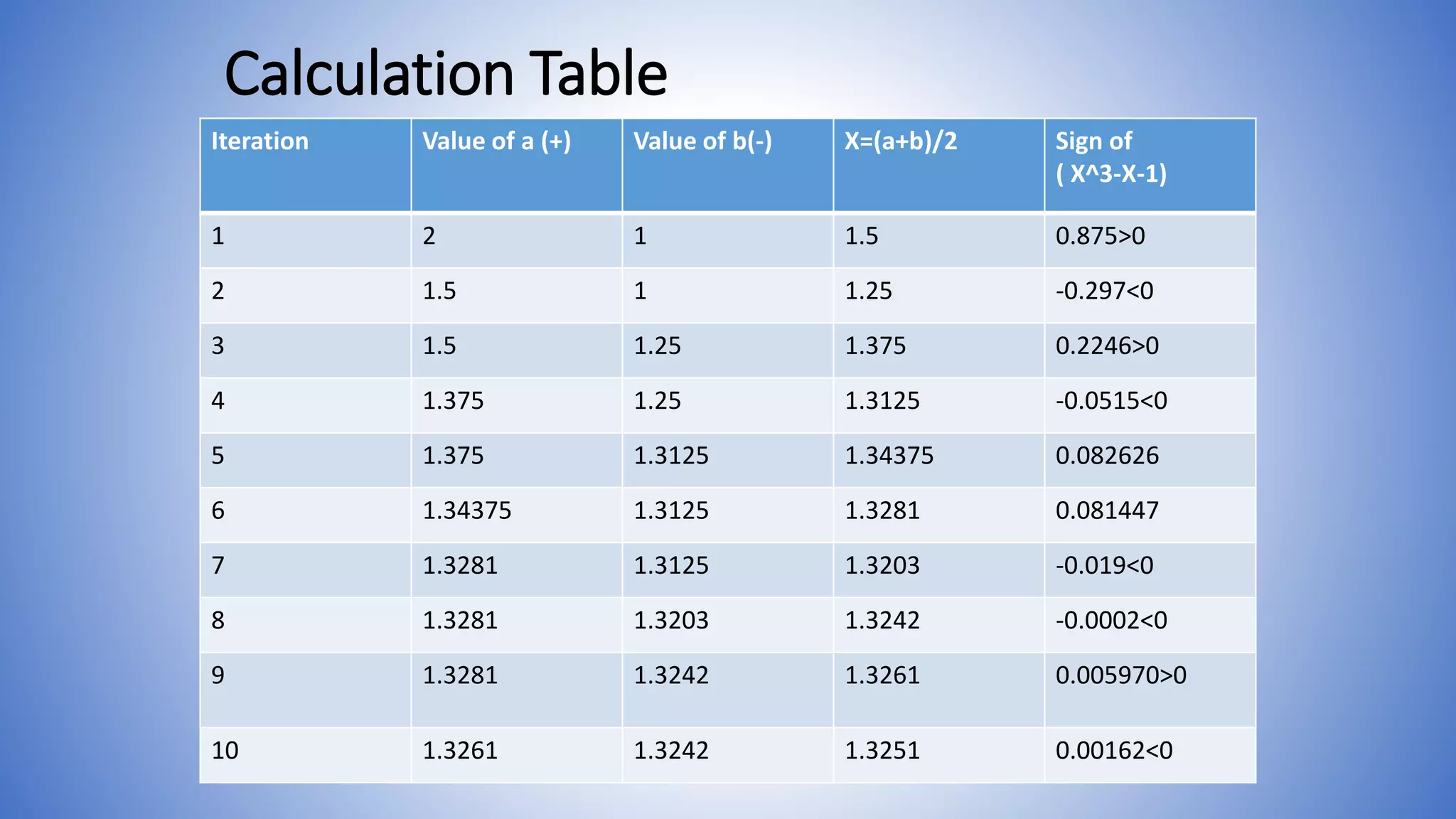
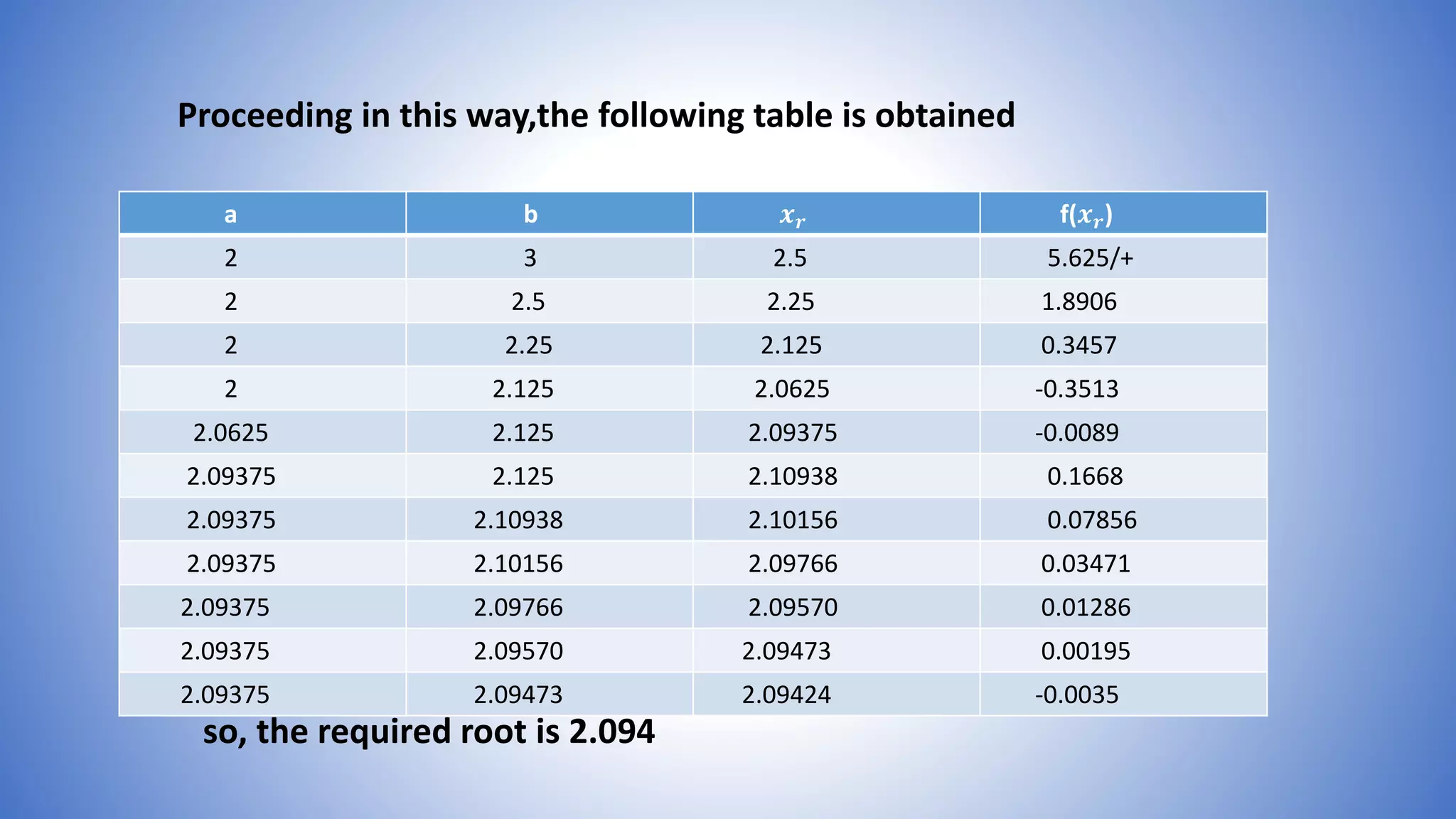
The bisection method is used to find the root of equations by repeatedly bisecting an interval and determining if the function value at the midpoint is positive or negative. The document provides examples of using the bisection method to find roots of equations like X^3-X-1, 4sinx-e^x, and X^2-4X-10. It shows calculating the function values at the endpoints of intervals, determining if the sign changes, bisecting the interval, and repeating until converging on the root.

1. Bisection Method

2. Find A Root of The Equation( X^3-X-1) using Bisection Method.
Solution:
Let f(X)= ( X^3-X-1)
Here,
F(1)=1-1-1=-1<0 and f(2)=8-2-1=5>0
Since f(1) and f(2) are of opposite sign to at least one real root lies between 1 and 2
.
X=(1+2)/2 =1.50

3. Calculation Table
Iteration Value of a (+) Value of b(-) X=(a+b)/2 Sign of
( X^3-X-1)
1 2 1 1.5 0.875>0
2 1.5 1 1.25 -0.297<0
3 1.5 1.25 1.375 0.2246>0
4 1.375 1.25 1.3125 -0.0515<0
5 1.375 1.3125 1.34375 0.082626
6 1.34375 1.3125 1.3281 0.081447
7 1.3281 1.3125 1.3203 -0.019<0
8 1.3281 1.3203 1.3242 -0.0002<0
9 1.3281 1.3242 1.3261 0.005970>0
10 1.3261 1.3242 1.3251 0.00162<0

4. • Find the root of the equation 𝐱 𝟑 − 𝟐𝐱 − 𝟓 = 𝟎 using bisection
method.
solution:
Let, f(x) = 𝒙 𝟑 − 𝟐𝒙 − 𝟓
Here, f(2) =-1
f(3) =16
So,the root lies in (2,3)
now ,𝒙 𝟏=
𝟐+𝟑
𝟐
=2.5; f(2.5)=5.625
So,the root lies in (2,2.5)
Again, 𝒙 𝟐=
𝟐+𝟐.𝟓
𝟐
=2.25; f(2.25)=1.8906
So,the root lies in (2,2.25)

5. Proceeding in this way,the following table is obtained
so, the required root is 2.094
a b 𝒙 𝒓 f(𝒙 𝒓)
2 3 2.5 5.625/+
2 2.5 2.25 1.8906
2 2.25 2.125 0.3457
2 2.125 2.0625 -0.3513
2.0625 2.125 2.09375 -0.0089
2.09375 2.125 2.10938 0.1668
2.09375 2.10938 2.10156 0.07856
2.09375 2.10156 2.09766 0.03471
2.09375 2.09766 2.09570 0.01286
2.09375 2.09570 2.09473 0.00195
2.09375 2.09473 2.09424 -0.0035

6. Find A Root of The Equation X^2-4X-10 using Bisection Method.
Solution:
Let f(X)=X^2-4X-10
Here,
f(-2)=4+8-10=2>0
& f(-1)=1+4-10=-5<0.
Since f(-2)is positive and f(-1) is negative so at least one real root lies
between -2 and -1.
So, X = (-2-1)/2
= -3/2
=1.5

7. Iteration a (+) b(-) 𝒙 𝒓 f(x)=x^2-4x-10
1 -2 -1 -1.5 -1.75<0
2 -2 -1.5 -1.75 0.0625>0
3 -1.75 -1.5 -1.625 -0.859<0
4 -1.75 -1.625 -1.6875 -0.40<0
5 -1.75 -1.6875 -1.7188 -0.1705<0
6 -1.75 -1.7188 -1.7344 -0.054<0
7 -1.75 -1.7344 -1.7422 0.004>0
8 -1.7422 -1.7344 -1.7383 -0.025<0
9 -1.7422 -1.7383 -1.7402 -0.0109<0
10 -1.7422 -1.7402 -1.7403 -0.003<0

8. Bisection Method:
Example
𝑓 𝑥 = 𝑥𝑒 𝑥
− 1 where, 𝜖 = 0.001
Here,𝑓 0 = −1
𝑓 1 = 1.7182
∴ 𝑥1 =
0 + 1
2
= 0.5
𝑓 0.5 = −0.1756
So, the root lies in 1, 0.5

9. Iteration 𝑎 b 𝑥 𝑟 𝑓(𝑥 𝑟)
1 1 0 0.5 -0.1756
2 1 0.5 0.75 0.5877
3 0.75 0.5 0.625 0.1676
4 0.625 0.5 0.5625 -0.0127
5 0.5625 0.5625 0.59375 0.0751
6 0.5625 0.5625 0.578125 0.0306
7 0.5625 0.5625 0.5703125 0.00877
8 0.5625 0.5625 0.56640625 -0.0023
9 0.5703125 0.56640625 0.5683594 0.00336
10 0.563594 0.56640625 0.5673828 0.000662

10. So, the root is 0.56
And,
∈=
𝑥10 − 𝑥9
𝑥10
× 100%
=
0.5673828 − 0.5683594
0.5673828
× 100%
= 0.172%

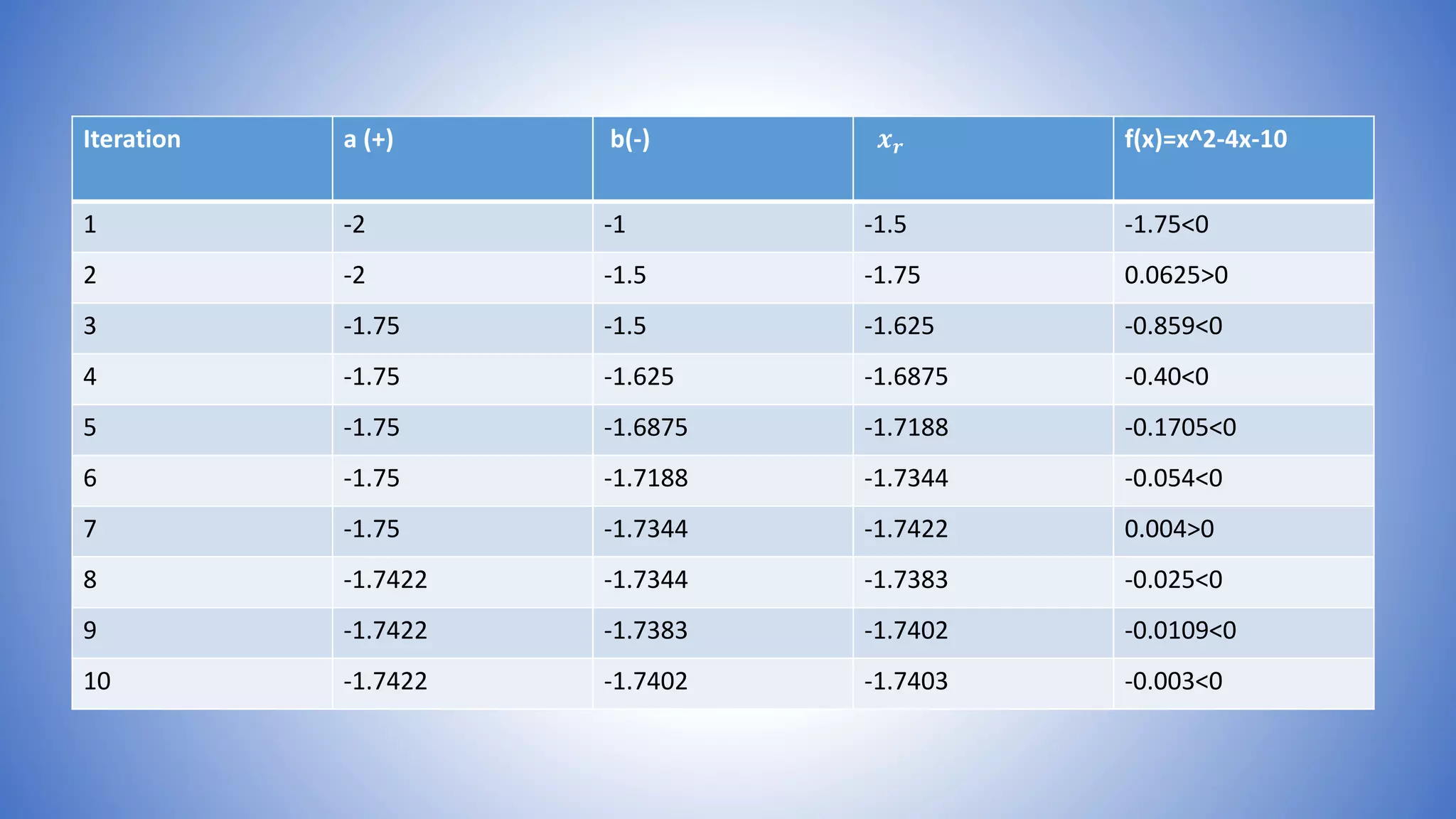
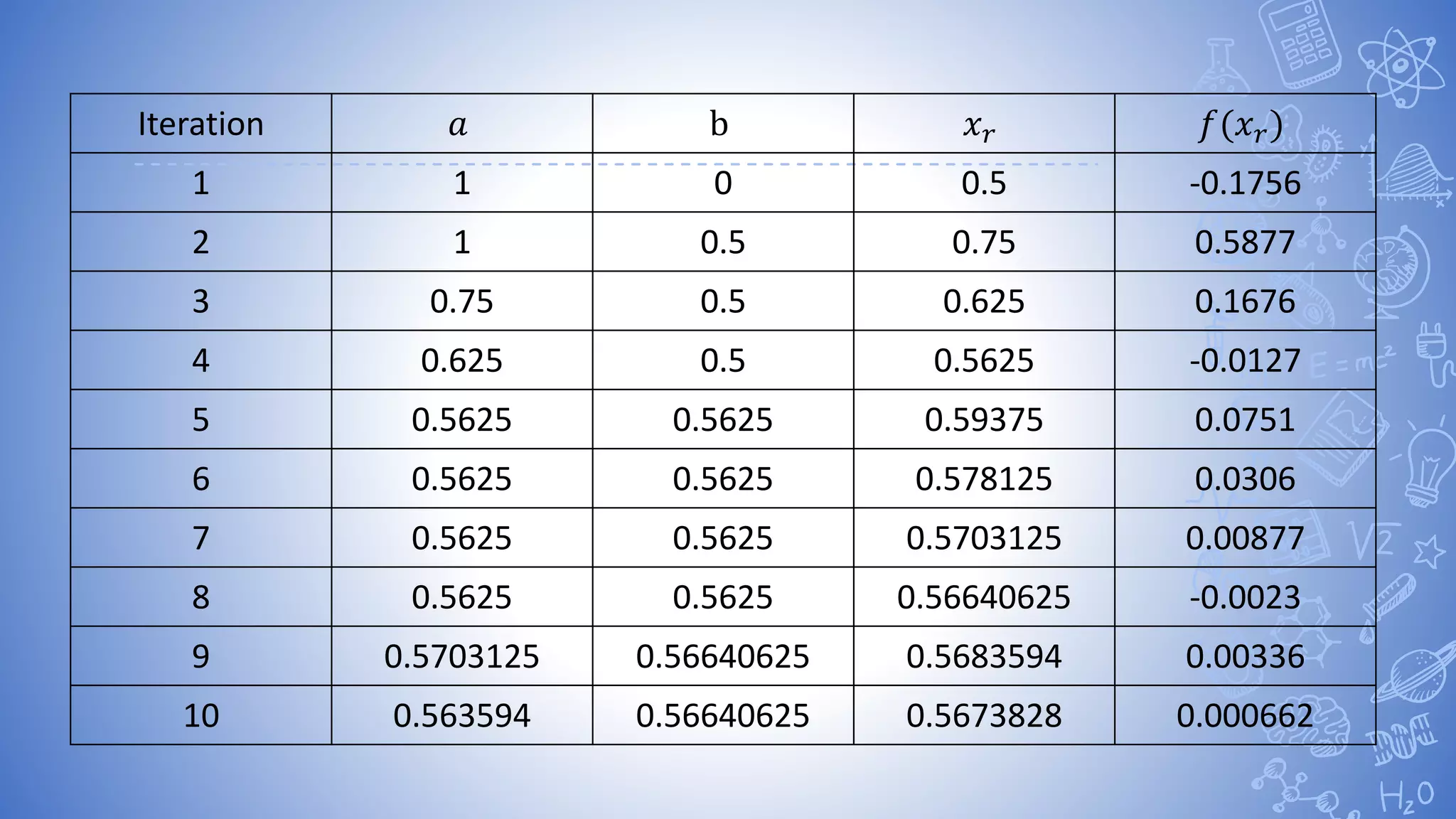
11. Example of Bisection Method
• Question:
• Find the root of the polynomial, g(x) = x3 - 5 + 3x using bisection
method. Where m = 1 and n = 2?
Solution: First find the value of g(x) at m = 1 and n = 2
g(1) = 13 - 5 + 3*1 = -1 < 0
g(2) = 23 - 5 + 3*2 = 9 > 0
Since function is continuous, its root lies in the interval [1, 2].

12. Example of Bisection Method
• Let t be the average of the interval i.e t = 1+22 = 1.5
• The value of the function at t is
• g(1.5) = (1.5)3 - 5 + 3*(1.5) = 2.875
• As g(t) is negative so n = 2 is replaced with t = 1.5 for the next
iteration. Make sure that g(m) and g(n) have opposite signs.

13. Example of Bisection Method

14. Find the root of the equation 4sinx-𝑒 𝑥=0 using bisection method.
solution:
let ,f(x) = 4sinx-𝑒 𝑥
Here, f(0) = -1
f(1) = 0.467
Since f(0)& f(1) are opposite sign So that at least 1 real root lies between 0 & 1
Therefore,x =
0+1
2
=0.5
Number of iterations for bisection method is given in the following table in arranged
way for determining the approximate value of the desired root of the given
equation.

15. So, the required root is 0.372
a b 𝒙 𝒓 f(𝒙 𝒓)
1 0 0.5 0.268
0.5 0 0.25 -0.294
0.5 0.25 0.375 0.0101
0.375 0.25 0.3125 -0.1371
0.375 0.3125 0.34375 -0.0621
0.375 0.34375 0.359375 -0.0256
0.375 0.359375 0.3671875 -0.0077
0.375 0.3671875 0.3710937 -0.00122
0.375 0.3710937 0.373046 0.00566
0.373046 0.3710937 0.372070 -0.00344
0.373046 0.372070 0.372558 0.00455
0.372558 0.372070 0.372279 0.0039
0.372279 0.372070 0.372174 0.0036
0.372174 0.372070 0.372122 0.0036