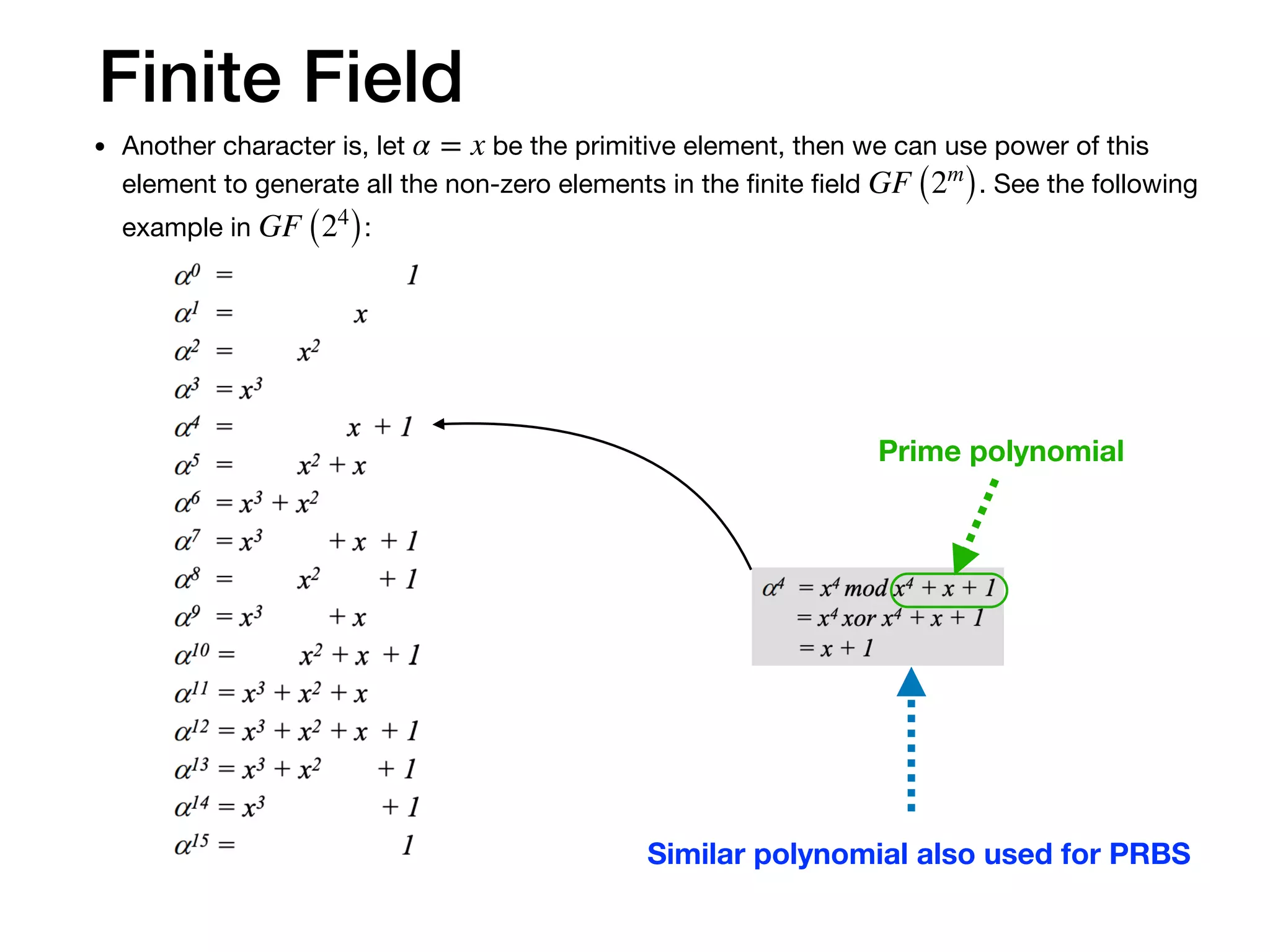
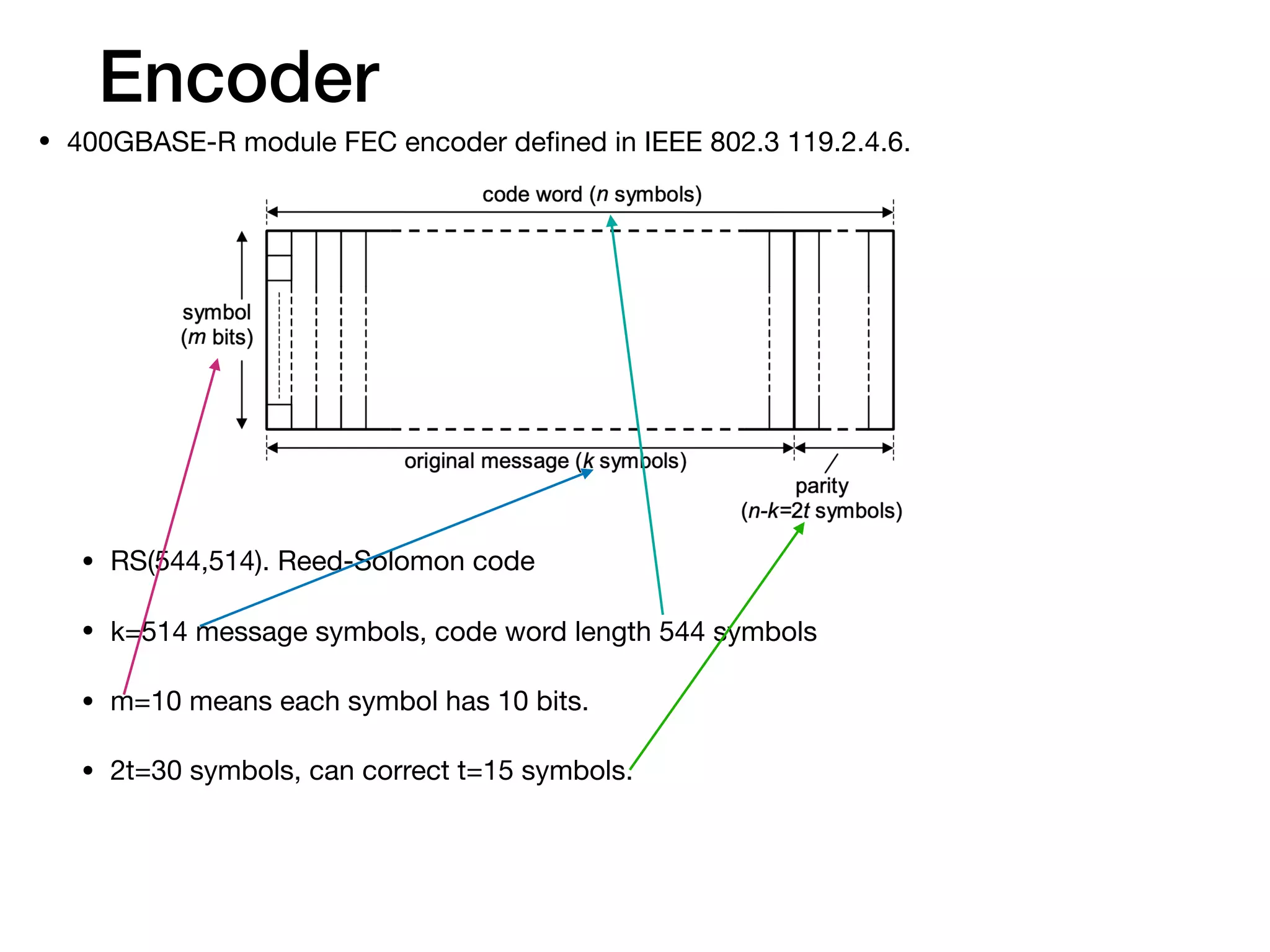
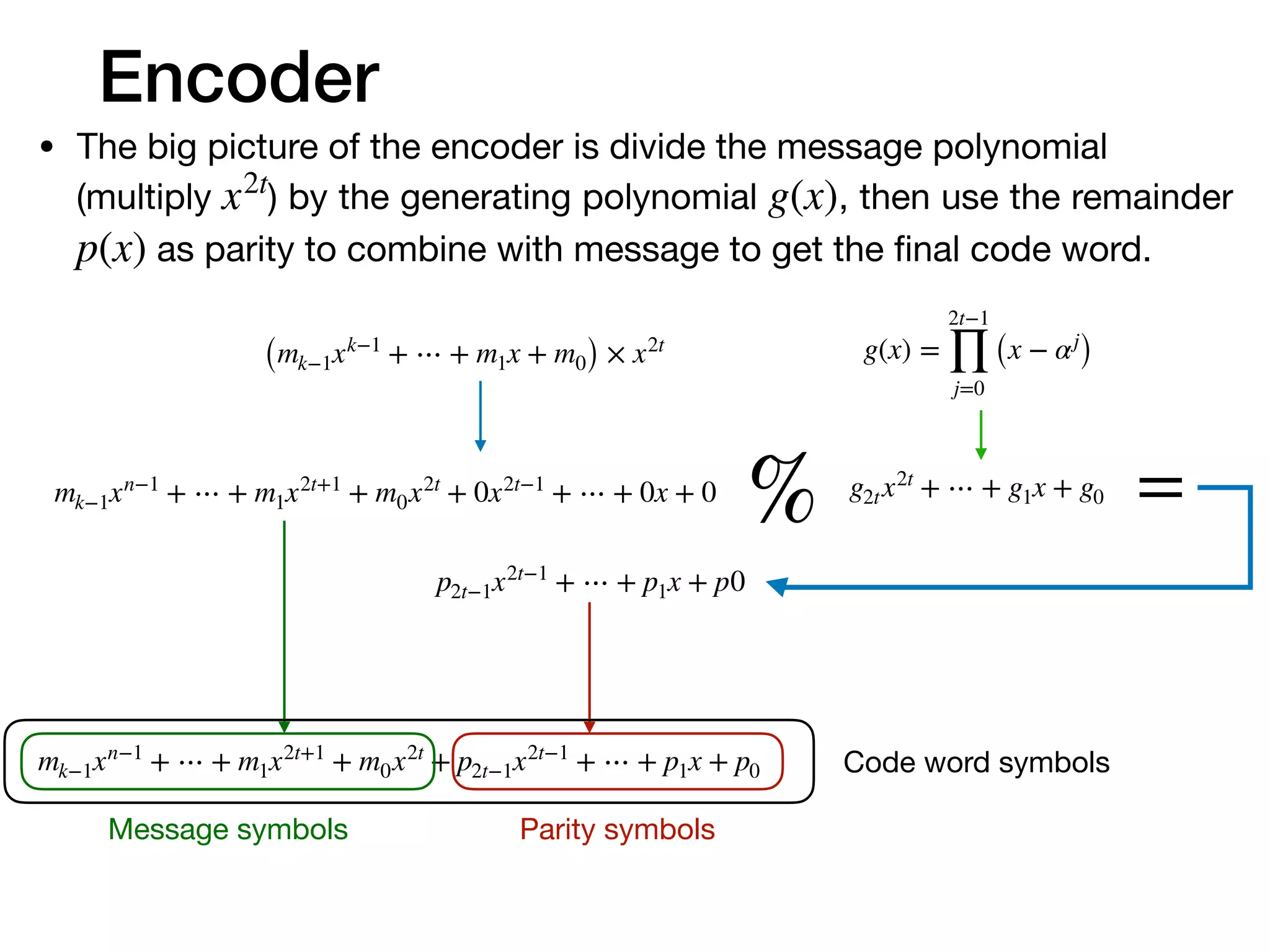
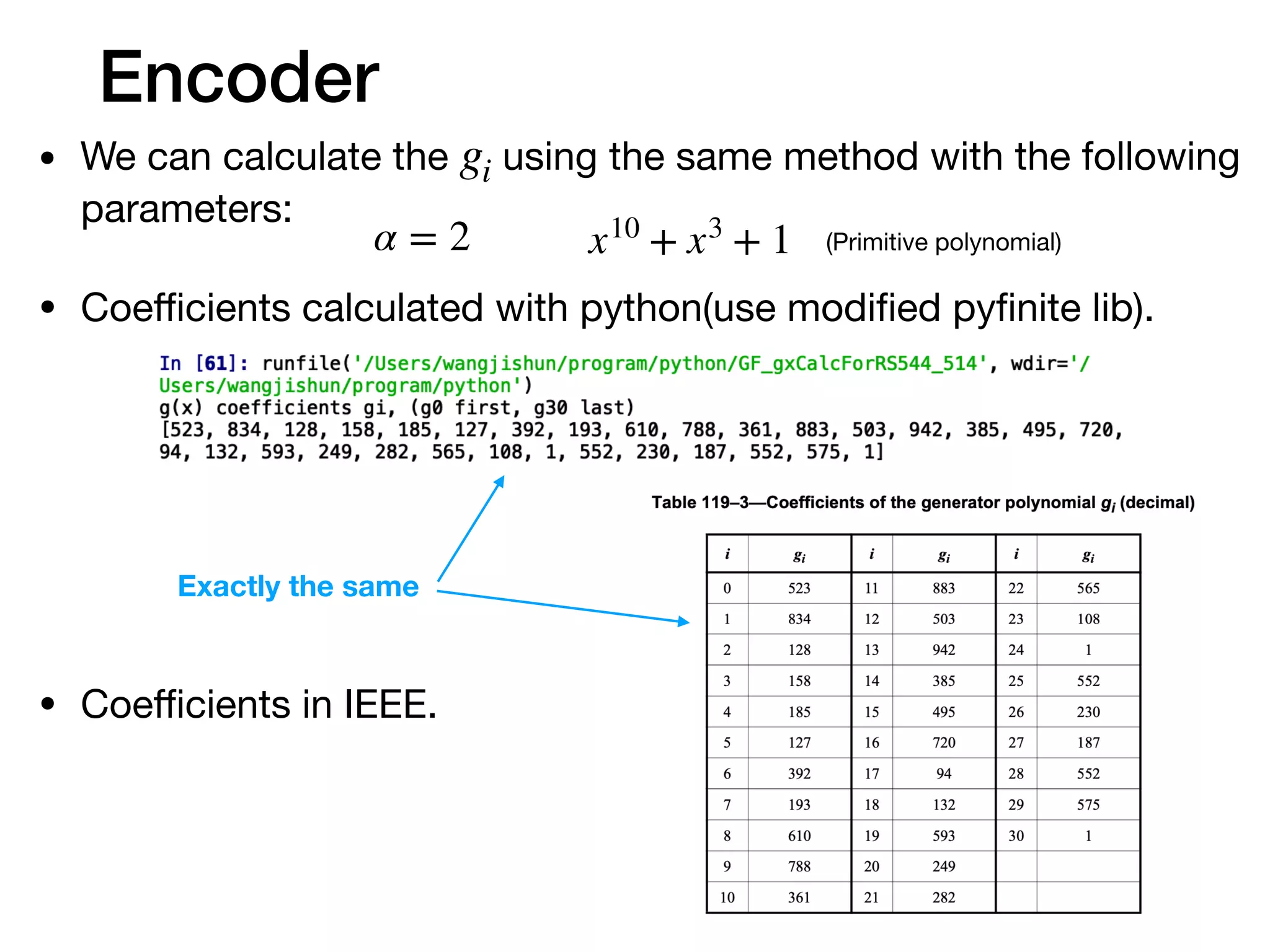
The document provides an in-depth explanation of Reed-Solomon coding, specifically the RS(544,514) code used in 200/400GBASE-R forward error correction. It details the mathematical foundations of finite fields and polynomial operations that underpin the encoding and decoding processes, including error correction strategies using syndromes, error locator polynomials, and error evaluation steps. Examples illustrate how to compute codewords from messages and reconstruct messages from corrupted codewords using the defined algorithms.

1. Understanding Reed-Solomon code
Jeffrey.Wang
2019.12.16

2. Abstraction
• Reed-Solomon code RS(544,514) is applied in 200/400GBASE-R
FEC(Forward Error Correction).
• The big picture of the coding math is like the following:
514-symbol
block
bits stream
514-symbol
message block
30-symbol
parity block
divide by and
keep the remainder
g(x)
544-symbol codeword block 544-symbol received block
Errors
Syndromes
Calculate the syndromes with g(x)
Error location
Error locator polynomial
544-symbol Corrected codeword
Error value
514-symbol message
drop parity block
Encoder Decoder

3. Finite Field
• Reed-Solomon algorithm is defined on finite field. So what is that?
• First of all, the ‘field’ is defined as a set with the following character:
• two operations ‘Addition’ and ‘Multiplication’ defined on it.
• closed on these operations.
• commutative, associative and distributive laws hold.
• additive and multiplicative identity elements.
• additive inverse for every element.
• multiplicative inverse for every non-zero element.
• ‘Real number’ set is a field.
• ‘Integer’ set is not a field. (e.g. Number 2 doesn’t have a
multiplicative inverse which is also an integer)

4. Finite Field
• The ‘Finite field’ is a field with finite elements, as it says in its
name. (Finite field is also called ‘Galois field’ named after
Evariste Galois (1811–1832))
• How can a field be ‘finite’? The key is ‘modulo’. Operations
become ‘addition with modulo ’ and multiplication with
modulo ’. ( is short for prime)
• An example, a finite field has 3 elements: 0, 1, 2.
Operations with modulo 3. The operations meet all the items in
field definition.
• or is a finite field if is a prime number.
p
p p
GF(3)
GF(p) GF(pm
) p
1 + 2 = 3 (mod 3) = 0
2 × 2 = 4 (mod 3) = 1

5. Finite Field
• About the prime number .
• integer set {0, 1, 2} is a finite field,
called . (3 is a prime number)
• integer set {0, 1, 2, 3} is not a finite
field, (4 is not a prime number),
because element 2 doesn’t have a
multiplicative inverse. So there’s
no .
• But we can make the field with 4
elements a finite field if we change the
rules a little
• a set with four elements {00, 01, 10,
11} is a finite field, called
p
GF(3)
GF(4)
GF(22
)
+ 0 1 2
0 0 1 2
1 1 2 0
2 2 0 1
x 0 1 2
0 0 0 0
1 0 1 2
2 0 2 1
+ 0 1 2 3
0 0 1 2 3
1 1 2 3 0
2 2 3 0 1
3 3 0 1 2
x 0 1 2 3
0 0 0 0 0
1 0 1 2 3
2 0 2 0 2
3 0 3 2 1
+ 00 01 10 11
00 00
01 10 11
01 01 00 11 10
10 10 11 00 01
11 11 10 01 00
x 00 01 10 11
00 00 00 00 00
01 00 01 10 11
10 00 10 11 01
11 00 11 01 10

6. Finite Field
• Here we introduce the ‘Polynomial’. We can use polynomials
to present the elements in with coefficients from
.
• Operations will be like the following: (Note that the
coefficients are from )
GF (2m
)
GF (2)
GF (2)
11000001 : x7
+ x6
+ 1 = 1x7
+ 1x6
+ 0x5
+ 0x4
+ 0x3
+ 0x2
+ 0x1
+ 1x0
Addition Multiplication

7. Finite Field
• Then we get back to the add and multiply operation matrix
in .
• Represent the elements with polynomials
• We should use modulo to keep the elements ‘finite’. And the
polynomial is used, which also called the
primitive polynomial.
• Take the red cell for example:
GF(22
)
x2
+ x + 1
+ 00 01 10 11
00 00
01 10 11
01 01 00 11 10
10 10 11 00 01
11 11 10 01 00
x 00 01 10 11
00 00 00 00 00
01 00 01 10 11
10 00 10 11 01
11 00 11 01 10 00 ⇒ 0x + 0
01 ⇒ 0x + 1
10 ⇒ 1x + 0
11 ⇒ 1x + 1
x + 1
× x
= x2
+ x (mod x2
+ x + 1)
= 1

8. Finite Field
• Another character is, let be the primitive element, then we can use power of this
element to generate all the non-zero elements in the finite field . See the following
example in :
α = x
GF (2m
)
GF (24
)
Similar polynomial also used for PRBS
Prime polynomial

9. Encoder
• 400GBASE-R module FEC encoder defined in IEEE 802.3 119.2.4.6.
• RS(544,514). Reed-Solomon code
• k=514 message symbols, code word length 544 symbols
• m=10 means each symbol has 10 bits.
• 2t=30 symbols, can correct t=15 symbols.

10. Encoder
• The big picture of the encoder is divide the message polynomial
(multiply ) by the generating polynomial , then use the remainder
as parity to combine with message to get the final code word.
x2t
g(x)
p(x)
mk−1xn−1
+ ⋯ + m1x2t+1
+ m0x2t
+ 0x2t−1
+ ⋯ + 0x + 0
% g2tx2t
+ ⋯ + g1x + g0
p2t−1x2t−1
+ ⋯ + p1x + p0
(mk−1xk−1
+ ⋯ + m1x + m0) × x2t
=
g(x) =
2t−1
∏
j=0
(x − αj
)
mk−1xn−1
+ ⋯ + m1x2t+1
+ m0x2t
+ p2t−1x2t−1
+ ⋯ + p1x + p0
Message symbols Parity symbols
Code word symbols

11. Encoder - Example
• Let’s take a simple example to look
into the division operation.
• Message is {1,2,3,4,5,6,7,8,9,10,11}
• Parity is {3,3,12,12}
• The final code word is
{1,2,3,4,5,6,7,8,9,10,11,3,3,12,12}
• Generating polynomial
• Prime polynomial is
• RS(15,11) on
g(x) = x4
+ 15x3
+ 3x2
+ x + 12
x4
+ x + 1
GF(24
)

12. Encoder
• IEEE gives the definition of generating polynomial .
• Use the simple one in last page to see how the calculation done.
g(x)
g(x) =
2t−1
∏
j=0
(x − αj
) = g2tx2t
+ ⋯ + g1x + g0
g(x) =
3
∏
j=0
(x − 2j
) = (x − 1) (x − 2) (x − 4) (x − 8)
= (x2
− 3x + 2) (x − 4) (x − 8)
= (x3
− 7x2
+ 14x − 8) (x − 8)
= (x4
− 7x3
+ 14x2
− 8x − 8x3
+ 13x2
− 9x + 12)
= x4
+ 15x3
+ 3x2
+ x + 12
7 × 8 = (x2
+ x + 1)x3
= x5 + x4 + x3
= x(x + 1) + (x + 1) + x3
= x2
+ x + x + 1 + x3
= x3
+ x2
+ 1
= 13
−7 − 8 = 7 + 8
= (x2
+ x + 1) + x3
= x3
+ x2
+ x + 1
= 15
• Keep in mind that all the addition and multiplication are defined in GF(24
)

13. Encoder
• We can calculate the using the same method with the following
parameters:
• Coefficients calculated with python(use modified pyfinite lib).
• Coefficients in IEEE.
gi
α = 2 x10
+ x3
+ 1
Exactly the same
(Primitive polynomial)

14. Encoder
• After we figure out all the detail of the calculation, let’s hold on a moment
to see what’s the mathematical idea behind the calculation.
• The final codeword is combined with message and parity symbols. And
the parity comes from the remainder. So the codeword can be divided by
. That means are roots of the codeword polynomial.g(x) αj
% = 0
2t−1
∏
j=0
(x − αj
)mk−1xn−1
+ ⋯ + m1x2t+1
+ m0x2t
+ p2t−1x2t−1
+ ⋯ + p1x + p0
Message symbols Parity symbols
C(x) = cn−1xn−1
+ ⋯ + c1x + c0
C(αj
) = CHT
= [c0 c1 ⋯ cn−1]
1 1 1 ⋯ 1
1 α1
α2
⋯ α2t−1
1 α2
α4
⋯ α(2t−1)2
⋯ ⋯ ⋯ ⋯ ⋯
1 αn−1
α2(n−1)
⋯ α(2t−1)(n−1)
= O1×2t
• Rewrite the equation in matrix

15. Encoder
• This equation means the codeword subspace is perpendicular
to the ’s row space.HT
[c0 c1 ⋯ cn−1]
1 1 1 ⋯ 1
1 α1
α2
⋯ α2t−1
1 α2
α4
⋯ α(2t−1)2
⋯ ⋯ ⋯ ⋯ ⋯
1 αn−1
α2(n−1)
⋯ α(2t−1)(n−1)
= O1×2t
• The encoder mapping the -dimensional original message into
-dimensional space. The -dimensional codeword subspace is
perpendicular to -dimensional subspace.
• If the transmission introduce any error make to , then
they’re not perpendicular any more. Then we know there are
errors, and maybe we can correct the errors.
k mk
n k
2t (2t = n − k)
C(x) R(x)

16. Decoder
• The result of is no longer Zero-matrix if there are errors.
• The result will be S. (short for Syndromes)
RHT
[r0 r1 ⋯ rn−1]
1 1 1 ⋯ 1
1 α1
α2
⋯ α2t−1
1 α2
α4
⋯ α(2t−1)2
⋯ ⋯ ⋯ ⋯ ⋯
1 αn−1
α2(n−1)
⋯ α(2t−1)(n−1)
= S
• We can correct the message if we know the error locations and
error values.

17. Decoder
• If there are errors.
• We can see that the ‘Syndromes’ are only affected by errors, no
matter what the codeword is.
• If there are errors and , then we can find the errors and
correct them.
• What we are going to do is to solve equations to get errors location
and errors value , with the known ‘Syndromes’
v v ≤ t
Xj Yj Si
R(x) = C(x) + E(x)
R(αi
) = C(αi
) + E(αi
) = 0 + E(αi
) = Si
Si = E(αi
)
= Y1αie1 + Y2αie2 + ⋯ + Yvαiev
= Y1Xi
1 + Y2Xi
2 + ⋯ + YvXi
v =
v
∑
j=1
YjXi
j

18. Decoder - Error locator
• Errors locator polynomial
• Since are roots of this equation
• With , we got equation group with equations.
And solve the equation group to get the coefficients
X−1
j
i = (0,1,⋯, v − 1) v
(Λ1, Λ2, ⋯, Λv)
Λ(x) = (1 + X1x)(1 + X2x)⋯(1 + Xvx)
= 1 + Λ1x + Λ2x2
+ ⋯ + Λvxv
0 = 1 + Λ1X−1
j + Λ2X−2
j + ⋯ + ΛvX−v
j
0 = YjXi+v
j + Λ1YjXi+v−1
j + ⋯ + ΛvYjXi
j
0 =
v
∑
j=1
YjXi+v
j +
v
∑
j=1
Λ1YjXi+v−1
j + ⋯ +
v
∑
j=1
ΛvYjXi
j
0 = Si+v + Λ1Si+v−1 + ⋯ + ΛvSi
Multiply YjXi+v
j
Add up for all j

19. Decoder - Error evaluation
• Get the roots of the locator equation, we got the error locations
.
• After substitute the error locations with solved values, here’s coming to the
final calculation: find the error values.
• Recover the codeword with error polynomial and drop the parity symbols. We
get the transmitted message.
• It’s better to go through all the calculation with our simple example. (P.S. the
algorithms for RS(544,514) are much more complex than in the simple
example)
(X1, X2, ⋯, Xv)
Xj
(1 + X1x)(1 + X2x)⋯(1 + Xvx) = 1 + Λ1x + Λ2x2
+ ⋯ + Λvxv
Si = Y1Xi
1 + Y2Xi
2 + ⋯ + YvXi
v
C(x) = R(x) − E(x)

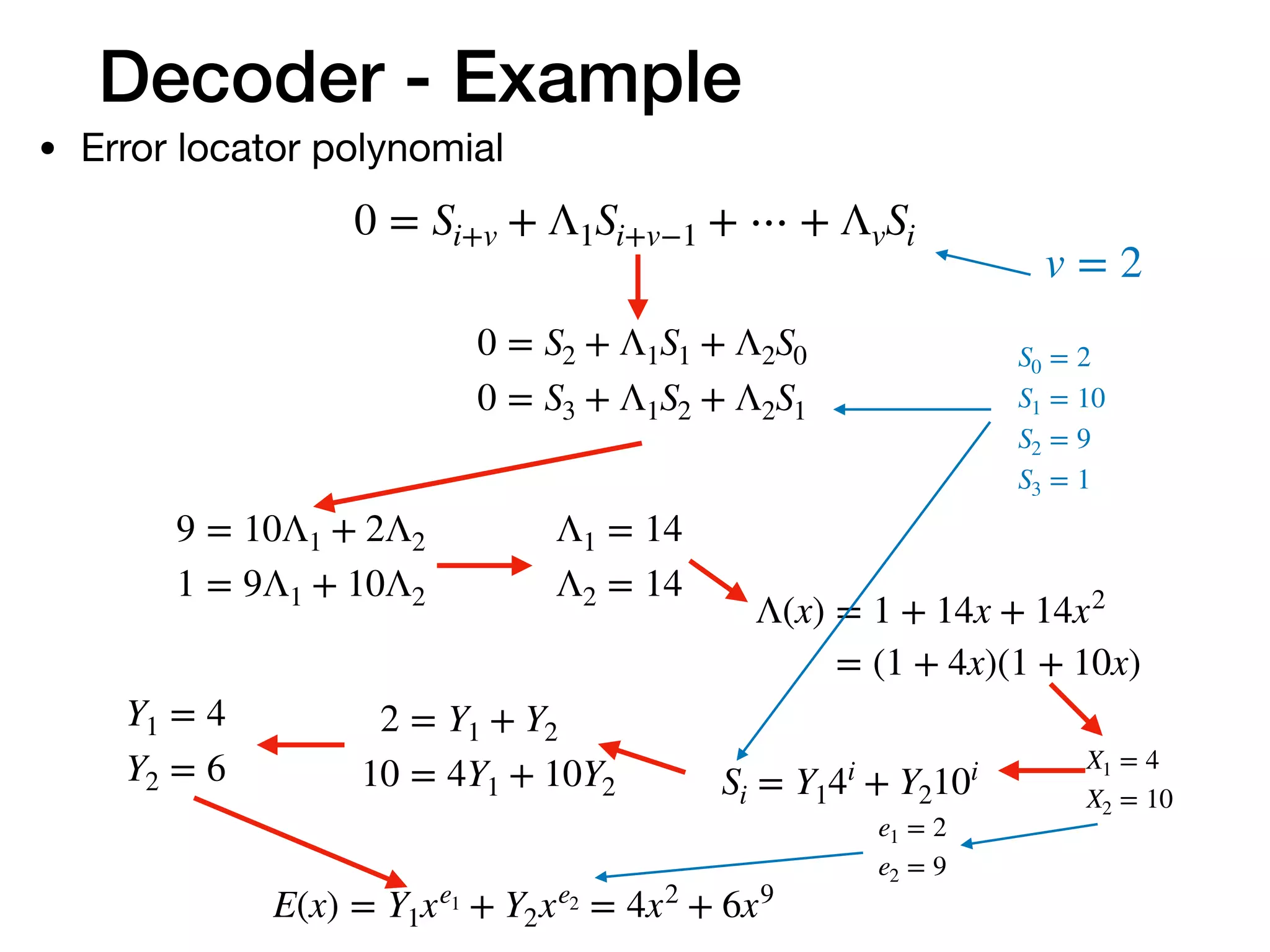
20. Decoder - Example
• First, use received symbols to get the ‘Syndromes’.
[12 12 7 3 11 10 9 8 7 0 5 4 3 2 1]
1 1 1 1
1 2 4 8
1 4 3 12
1 8 12 10
1 3 5 15
1 6 7 1
1 12 15 8
1 11 9 12
1 5 2 10
1 10 8 15
1 7 6 1
1 14 11 8
1 15 10 12
1 13 14 10
1 9 13 15
= [2 10 9 1]
errors
Syndromesreceived codeword
parity check matrix
Here we use the parity check matrix. Divide the codeword
with with do the same thing.g(x)

21. Decoder - Example
• Error locator polynomial
0 = Si+v + Λ1Si+v−1 + ⋯ + ΛvSi
v = 2
0 = S2 + Λ1S1 + Λ2S0
0 = S3 + Λ1S2 + Λ2S1
S0 = 2
S1 = 10
S2 = 9
S3 = 1
9 = 10Λ1 + 2Λ2
1 = 9Λ1 + 10Λ2
Λ1 = 14
Λ2 = 14
Λ(x) = 1 + 14x + 14x2
= (1 + 4x)(1 + 10x)
Si = Y14i
+ Y210i
2 = Y1 + Y2
10 = 4Y1 + 10Y2
Y1 = 4
Y2 = 6
E(x) = Y1xe1 + Y2xe2 = 4x2
+ 6x9
X1 = 4
X2 = 10
e1 = 2
e2 = 9

22. Decoder - Example
• Decode finish
E(x) = 6x9
+ 4x2
R(x) = 1x14
+ 2x13
+ 3x12
+ 4x11
+ 5x10
+ 0x9
+ 7x8
+ 8x7
+ 9x6
+ 10x5
+ 11x4
+ 3x3
+ 7x2
+ 12x + 12
C(x) = 1x14
+ 2x13
+ 3x12
+ 4x11
+ 5x10
+ 6x9
+ 7x8
+ 8x7
+ 9x6
+ 10x5
+ 11x4
+ 3x3
+ 3x2
+ 12x + 12
[1 2 3 4 5 6 7 8 9 10 11]

23. Reference
• IEEE 802.3 119.2.4.6
• https://content.sakai.rutgers.edu/access/content/user/ak892/
Reed-SolomonProjectReport.pdf
• SC390 Introduction to Forward Error Correction, Frank
Kschischang, Univ. of Toronto, Canada.
• https://users.math.msu.edu/users/jhall/classes/codenotes/
GRS.pdf
• http://downloads.bbc.co.uk/rd/pubs/whp/whp-pdf-files/
WHP031.pdf