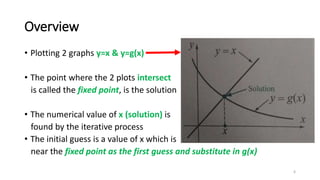
This document discusses the fixed point iteration method for solving nonlinear equations numerically. It begins with an overview of the method, explaining that it involves rewriting equations in the form x=g(x) and then iteratively calculating xn+1=g(xn) until convergence. The document then provides an example of using the method to solve the equation x3+x2-1=0. It shows rewriting the equation, choosing an initial guess, iteratively calculating the next value of x, and checking for convergence. The document concludes by explaining how to implement the fixed point iteration method numerically using loops in code.

1. NUMERICAL METHODS LAB
(MT-202L)
Instructor: Engr. Ahmed Zaheer
Batch: 2k19 (5th Semester)
Session: Fall 2022
MED, HITEC University, Taxila

2. Fixed Point Iteration Method
2

3. OVERVIEW
3

4. What is it?
• A method for solving NON-LINEAR EQUATIONS
• Non-linear Equations (some examples):
• 4𝑥2 − 1 = 0
• 𝑥3 −𝑥2 +10 = 0
• 𝑦 = sin(𝑥)
• 𝑦 = log(𝑥)
4

5. Overview
• This is also called as Methods of successive substitution
• We solve f(x) = 0 in a different way
• Actually we solve x= g (x)
• Now we can write the above as x-g(x) = 0
• x-g(x) can now be called f(x)
xn+1 = g(xn)
• g(x) is also called the iteration function
5

6. Overview
• Plotting 2 graphs y=x & y=g(x)
• The point where the 2 plots intersect
is called the fixed point, is the solution
• The numerical value of x (solution) is
found by the iterative process
• The initial guess is a value of x which is
near the fixed point as the first guess and substitute in g(x)
6

7. Explanation
• Consider the equation: 𝒙𝟑 + 𝒙𝟐 − 𝟏 = 𝟎
• This equation can be written as: 𝑓 𝑥 = 𝑥3 + 𝑥2 − 1
• For x = 0, f(x) = -1
• For x = 1, f(x) = 1
• Solution (ROOT) of the equation will lie between -1 & 1 (b/c of changing sign)
• INITIAL GUESS: 𝑥0 = 0.5 (some other value could also be taken)
7

8. Explanation
• Equation: 𝒙𝟑 + 𝒙𝟐 − 𝟏 = 𝟎
• Equation can be rearranged as:
1. 𝑥 =
3
1 − 𝑥2 [ g(x) =
3
1 − 𝑥2 ]
2. 𝑥 = 1 − 𝑥3 [ g(x) = 1 − 𝑥3 ]
3. 𝑥 = 1/ 𝑥 + 1 [ g(x) = 1/ 𝑥 + 1 ]
• Which one of these “g(x)” is the correct one?
8

9. Explanation
• Equation: 𝒙𝟑 + 𝒙𝟐 − 𝟏 = 𝟎
• Which one of these “g(x)” is the correct one?
• CONDITION FOR CHECKING
|
𝒅[𝒈(𝒙)]
𝒅𝒙
| = |𝒈′
𝒙 | < 𝟏
The absolute value (i.e. positive value) of 1st differential of g(x) should be less
than 1 for the g(x) to be valid.
9

10. Explanation
• Equation: 𝒙𝟑
+ 𝒙𝟐
− 𝟏 = 𝟎
• g(x) = 1/ 𝑥 + 1 : This is the desired g(x)
• Generalized Form: 𝒙𝒏+𝟏 =
𝟏
𝟏+ 𝒙𝒏
10
g(x) =
𝟑
𝟏 − 𝐱𝟐 g(x) = 𝟏 − 𝐱𝟑 g(x) = 𝟏/ 𝐱 + 𝟏
𝑔′
𝑥 =
−2𝑥
3(1 − 𝑥2)2/3 𝑔′
𝑥 =
−3𝑥2
(1 − 𝑥3)1/2
𝑔′
𝑥 =
−1
2(𝑥+1)3/2
g’(0.5) = -0.4038 g’(0.5) = -0.8018 g’(0.5) = -0.2722
|g’(x)| = 0.4038 (< 1) |g’(x)| = 0.8018 (< 1) |g’(x)| = 0.2722 (< 1)
Good OK Best (minimum value of
g’(x) at 𝒙𝟎)

11. Explanation
• Equation: 𝒙𝟑 + 𝒙𝟐 − 𝟏 = 𝟎
• g(x) = 𝒙𝒏+𝟏 =
𝟏
𝟏+ 𝒙𝒏
• Root of Equation: 0.75488
11
i 𝒙𝒊 𝒙𝒊+𝟏 = 𝒈(𝒙)
0 0.5 0.81650
1 0.81650 0.74196
2 0.74196 0.75767
3 0.75767 0.75428
5 0.75428 0.75501
6 0.75501 0.75485
7 0.75485 0.75488
8 0.75488 0.75488

12. BUILT-IN FUNCTIONS
12

13. fzero:
Built-in Command
• This command is built into the MATLAB specifically to solve Non-Linear Equations.
• MATLAB can only equations in which right-hand side of the equal-sign is Zero.
• Consider the equation: 𝒙𝟑
+ 𝒙𝟐
− 𝟏 = 𝟎
• Equation can be written as: 𝑓 𝑥 = 𝑥3 + 𝑥2 − 1
• f(x) can be written in MATLAB as: f=@(x)
• This equation will be written and solved in MATLAB as:
• f=@(x) (x^3 + x^2 -1)
• root = fzero(f,1)
13

14. fzero:
Built-in Command
• Equation: 𝑓 𝑥 = 𝑥3 + 𝑥2 − 1
• This equation will be written and solved in MATLAB as:
• f=@(x) (x^3 + x^2 -1)
• fzero (f , 1) % This command will find the root of Function “ f ”, with Initial Guess value = 1
(Guess value can be changed to get the correct answer, or to get multiple roots)
• Output will be displayed as: ans = 0.7549
14

15. Graphical Solution
• Graphs can be used to estimate the solution of equations
15

16. Graphical Solution
• Equation: 𝒙𝟑 + 𝒙𝟐 − 𝟏 = 𝟎
• 𝑦 = 𝑥3 + 𝑥2 − 1
• 𝑦 = 𝑥
• Graphs can be drawn in MATLAB as:
x = -10:0.1:10;
% x is an array containing elements from -10 to +10, with incremental steps of 0.1
y1 = x.^3 + x.^2 - 1;
y2 = x;
plot(x,y1,x,y2) % For plotting multiple graphs using a single line of code
hold on
grid on
legend('y1','y2')
16

17. Graphical Solution
• Equation: 𝒙𝟑 + 𝒙𝟐 − 𝟏 = 𝟎
• 𝑦 = 𝑥3 + 𝑥2 − 1
• 𝑦 = 𝑥
• This graph can be zoomed for
better clarity.
• The point where the two curves
intersect, is the solution i.e.
the required
Root of the equation.
17

18. CODING THE ITERATION METHOD
18

19. Overview
• Iterative procedure for finding the root of an equation consists of 3
parts:
1. Initial Guess of solution
2. Algorithm for finding approximate solution
3. Criteria to Stop Computations
• Equation: 𝒙𝟑 + 𝒙𝟐 − 𝟏 = 𝟎
• g(x) = 𝒙𝒏+𝟏 =
𝟏
𝟏+ 𝒙𝒏
19

20. For Loop
x0 = 1; % Intial Guess value
maxIter = 50; % No. of max. iterations
tolX = 1e-4; % Tolerance limit for Error
x = x0; % x_n+1
x_old = x0; % x_n
for i = 1:maxIter % For Loop
x = 1/sqrt(1+x); % g(x)
fprintf('x%0.0f = %fn',i,x) % Output display
err = abs(x - x_old); % Absolute (positive) value of Error (between x_n and x_n+1)
x_old = x; % Updating value of x_n
if err < tolX % Comparing Error with Tolerance Limit
break % When Error becomes less than Tolerance, the Loop will break
end % End of If
end % End of For Loop 20
Output Display
x1 = 0.707107
x2 = 0.765367
x3 = 0.752632
x4 = 0.755361
x5 = 0.754774
x6 = 0.754900
x7 = 0.754873

21. While Loop
x0 = 1; % Intial Guess value
maxIter = 50; % No. of max. iterations
tolX = 1e-6; % Tolerance limit for Error
err = 1; % Intial value of Error
x = x0; % x_n+1
x_old = x0; % x_n
i = 1; % Intial value of i (i=0,1,2,...)
while err > tolX % While Loop
x = 1/sqrt(1+x); % g(x)
fprintf('x%0.0f = %fn',i,x) % Output display
i = i+1; % Updating value of i
err = abs(x - x_old); % Positive value of Error (between x_n and x_n+1)
x_old = x; % Updating value of x_n
end % Loop will end when Error becomes less than Tolerance 21

22. CONCLUSION
22

23. Review
• Fixed Point Iteration Method is used for finding ROOTS of Non-Linear Equations.
• fzero command can be used to find solution of Non-linear equations directly
(Initial Guess value should be chosen carefully).
• Graphs can be used to visualize the solution of the equation.
• Loops (both For & While) are tools which can be implemented in program code to
find solution of equations, with following steps:
• Initial Guess value
• Algorithm for finding solution
• Criteria for stopping computations
23

24. The End
• Thank you!
• Any Questions?
24