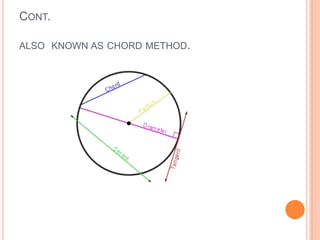
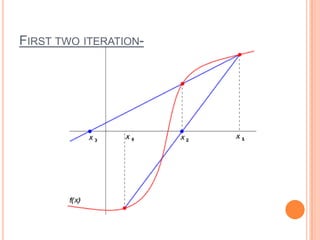
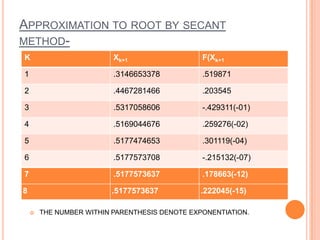
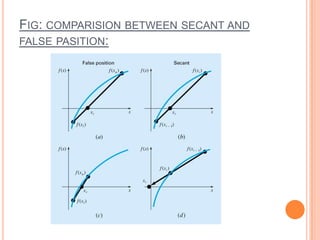
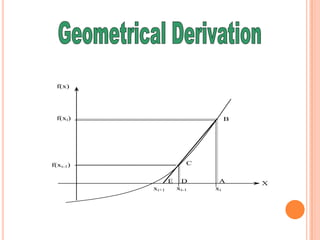
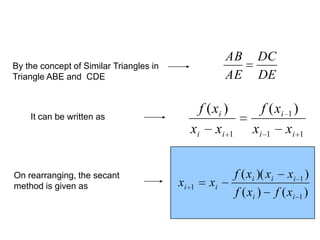
The secant method is a root-finding algorithm that uses successive secants of a function to linearly approximate the root. It requires two initial guesses, x0 and x1, to construct a secant line through the points (x0, f(x0)) and (x1, f(x1)). The x-intercept of this line provides the next approximation x2. Repeating this process iteratively refines the approximation until the root is found to within a desired precision. The secant method converges faster than bisection near roots and does not require evaluating derivatives, but it may fail to converge for some functions.

1. Presentation on secant methodPRESENTED BY:-RITU NAMDEOM.C.A. 2 ND SEM ‘B’ SEC

2. SECANT METHODThe word secant comes from the Latin secare, means to cut.

3. It is a root finding method.

4. Root :-The roots (sometimes also called "zeros") of an equation are the values of for which the equation is satisfied. e.g f(x)=0 The secant method is not a bracketing method , because it not required to change signs between estimates. Cont.also known as chord method.

5. methodStarting with initial values x0 and x1, we construct a line through the points (x0,f(x0)) and (x1,f(x1)), x = x1- f(x1)* (x1-x0) f(x1)-f(x0)We then use this value of x as x2 and repeat the process using x1 and x2 instead of x0 and x1. We continue this process, solving for x3, x4, etc., until we reach a sufficiently high level of precision (a sufficiently small difference between xn and xn-1).

6. Cont.This new value replaces the oldest x value being used in the calculation....

7. First two iteration-

8. Example-Question- Use the secant method to determine root of equation.cos x-x ex=0 solution- Taking the initial approximation as x0=0 ,x1=1 we have for secant method f(0)=1 and f(1)=cos1-e=-2.177979523

9. Approximation to root by secant method-THE NUMBER WITHIN PARENTHESIS DENOTE EXPONENTIATION.ADVANTAGES OF SECANT METHODIt does not require the computation of the first order derivative.

10. No need to check for sign.

11. Sometimes it is good to start finding a root using the bisection method then once you know you are close to the root you can switch to the secant method to achieve faster convergence.

12. when the method converges it can be shown to have an order of convergence which is: =1.618 (known as golden ratio )The secant method converges more rapidly near a root.Drawback of secant methodBecause the secant method is not a bracketing method it may not converge.

13. Another problem of this method that does not know when to stop. It must be performed several times until the f of the current guess is very small.

14. If the function is very “flat” the secant method can fail.Secant Method: FailureEX-Secant method1oldestfirst iteration0.5f(x)000.511.522.533.54previousnew-0.5second iteration-11.11x

15. 1.12Secant Method: FailureThe numerical values associated with the “failure” example are:

16. Regulafalsivs secantIt is similar to regula falsie except:-Condition f(x1).f(x2)<0Will convergence always. speed can be slow. No need to check for sign.Begin with a, b, as usual.Regula falsie a variant of the secant method which maintains a bracket around the solution. secant method keeps the most recent two estimates, while the false position method retains the most recent estimate and the next recent one which has an opposite sign in the function value.

17. Fig: comparision between secant and false pasition:

18. Secant vsnewtonraphsonA slight variation of Newton’s method for functions whose derivatives are difficult to evaluate.

19. The secant method has the same properties as Newton’s method. Convergence is not guaranteed for all xo.

20. Similar to Newton-Raphson except the derivative is replaces with a finite divided difference.Applications:-The Secant Method is one of a number of analytical procedures available to earthquake engineers today for predicting the earthquake performance of structures.Designing of multi-story building.