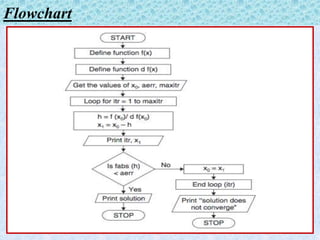
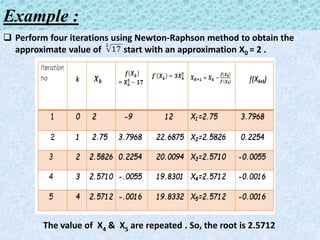
The document presents a study on the Newton-Raphson method, detailing its history, derivation, and applications in numerical analysis. It explains the method's advantages, such as faster convergence and applicability to various equations, while also acknowledging its disadvantages like higher computational demands. The presentation concludes that the Newton-Raphson method is effective for finding roots of equations with reduced time complexity.

1. Presented by
M.Sc 2nd semester (Group-4)
Dipankar Saha Soujanita Dey Nirnay Banik
Id : 20IUT0080023 Id : 20IUT0080024 Id : 20IUT0080028
Debajyoti Banik Aratrika Banik Satashree Deb
Id : 20IUT0080029 Id : 20IUT0080031 Id : 20IUT0080032
A brief study on Newton-Raphson
Method
Department of Physics, ICFAI
University ,Agartala, West Tripura.

2. Acknowledgment
Itisgreatpleasureforustoundertakethispresentation.wefeel highlydoingthis
presentation namely“Abrief studyonNewton-RaphsonMethod”.
Wewould liketoexpressourspecialthanksof gratitudetoourNumerical
Analysisteacher“Mr.SubalRanjanSahu”forhisheartfulrestless assistincompletingthis
presentation.
Thispresentation wouldnothavecompletedwithouthisenormoushelpandworthy
experiences.Wheneverwewereinneed,hewastherebehindusalways.
DATE: GROUP-4
9th June,2021 M.ScPhysics,2nd semester
ICFAIUniversityTripura.

3. Overview
 Introduction.
 History Of Newton-Raphson Method.
 Derivation.
 Graphical representation.
 Taylor- Series Expansion.
 Example.
 Rate of convergence of N-R method.
 Algorithm.
 Flowchart.
 MATLAB code.
 Advantages & Disadvantages.
 Applications.
 Conclusion.

4. Introduction
In Numerical Analysis Newton-Raphson Method, also
known as the Newton’s Method, is a method for finding
successively better approximations to the roots of a real
valued function.
 In Newton’s method the root is not bracketed , In fact, only
one initial guess of the root is needed to get the iterative
process started to find the root of an equation. The method
hence falls in the category of open methods.

5. History Of Newton-Raphson Method
 Heron of Alexandria (10-7- AD) described a method
(called Babylonian Method) to iteratively
approximate a square root.
 Francois Viete(1540-1603) developed a method to
approximate roots of polynomials.
 Isaac Newton (1540-1603) in 1669 (PUBLISHED IS
1711) improved upon Viete’s method.
A simplified version of Newton’s method was
published by Joseph Raphson (1648-1715) in 1690.
Though, Newton (and Raphson) did not see the connection between his
method and calculus.
 The modern treatment is due to Thomas Simpson (1710-1761).
Isaac Newton

6. Derivation
The Newton Raphson method is based on the principle that if the
initial guess of the root is at Xn ,
Then if one draws the tangent to the curve at f(Xn) , the point Xn+1
where the tangent cross the X-axis is an improve estimate of the root
(shown in the figure-1).
From the equation of slop we have,
This is the starting point at X0 , so we write it as
Similarly ,

7. Thus we get the general formula,
…………………(i)
Equation (i) is called the Newton-Raphson formula
for solving nonlinear equation of the form f(X)=0.
One can repeat this process until one find the root
within a desirable tolerance.

8. Graphical representation
Figure-1: Graphical representation for N-R Method

9. Taylor Series Expansion:-
we have given an equation f(x)=0 and x0 be the approximated root
of the given equation.
Let (X0+h) be the actual root where ‘h’ is very small such that
f(X0+h)=0 ……….(ii)
Now from Taylor Series expansion on expanding to f(X0+h) we get,
Now on neglecting higher powers of h we have,
From Eqn.(ii)

10. Hence 1st approximation X1=(X0+h)
On repeating this process we get,
This is the required Newton-Raphson Method.
2nd approximation

11. Example :
 Perform four iterations using Newton-Raphson method to obtain the
approximate value of start with an approximation X0 = 2 .
The value of X4 & X5 are repeated . So, the root is 2.5712

12. Rate of Convergence of N-R method:
We have the N-R formula
Let, at x=α we have the exact root of a given equation f(x)=0
& ‘ϵ ’ be the error .
On substituting Xn=α+ϵn and Xn+1= α+ϵn+1 in equation (i) we get

13. Neglecting higher power of ϵn and noting also f(α)=0 we have
[neglecting higher order term]
Thus we see that the rate of convergence of N-R method is 2.
ϵn+1 proportional to ϵn
2

14. Algorithm
• Define the function.
• Choose an initial guess X0 such that, [a,b] be any interval in
which f(a)<0 & f(b)>0 , then
• Then
• If f(X1) = 0, then X1 is our exact root.
• For more accuracy by repetition of this process we can find X2
,X3 , X4………. from X1 until we are getting the accurate value of
the root.

15. Flowchart

16. MATLAB CODE
This is the code which we used while using programming
clear all
close all
clc
f=@(x) f(x) ; %define function
df = @ˊ(x) fˊ(x) ; %define derivative of the function
a= input('First guess a='); %initial guess
b= input('Second guess b='); %initial guess
n = input('number of iterations=');
while f(a)*f(b)>0
disp('initial guesses are not correct')
a = input('a=');
b = input('b=');
end
x=a;

17. MATLAB CODE
fprintf('iteration table for newton raphson methodn')
fprintf('n iteration no xt f(x)t df(x)tn')
for i = 1:n
x(i)= x- (f(x)/df(x));
f(x);
df(x);
x=x(i);
fprintf('n%d %13.4f %13.4f %13.4f %13.4fn',i,x,f(x),df(x))
end
fprintf('solution of the equation =%f',x)

18. Advantages & Disadvantages
Advantages
• The Newton-Raphson method is faster, more reliable
and the results are accurate.
• Requires less number of iterations for convergence.
• Suitable for large system.
Disadvantages
• The programming logic is more.
• Memory requirement is more.
• Computational time per iteration is higher due to larger
number of calculations per iteration .

19. Applications
 Using the Newton-Raphson formula we can find the roots
of the Algebraic equations and as well as Transcendental
equations in less time as well as less number of iterations.
 Usually used in computer science for root algorithm.
 Used for Multidimensional root finding.
 Solving practical technical problems using scientific and
mathematical tools.

20. Conclusion
 Root finding is also one of the problems in practical
applications. To solve the transcendental equations most of
the times we use the iteration methods. There are so many
iteration methods like Newton-Raphson method.
We concluded that, the convergence rate of Newton-
Raphson method is fast as compared to other methods.
The effectiveness of using scientific calculator in solving
non-linear equations using Newton-Raphson method also
reduces the time complexity, for solving nonlinear
equations.
So, we also concluded that the Newton-
Raphson method can be used very effectively to determine
the correct & accurate root in less time as well as less
number of iterations.

21. Bibliography
• Numerical analysis and computational procedures
by S.A.MOLLAH.
• Introductory numerical analysis by N.DATTA &
R.N.JANA.
• Numerical methods by M.K.Jain,S.R.K.lyengar &
R.K.Jain.
• Introductory methods of numerical analysis by
S.S.Sastry.
• An introduction to numerical analysis by Kendall
E.Atkinson.