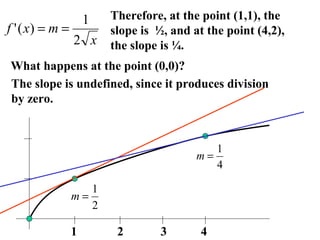
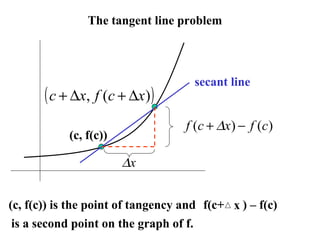
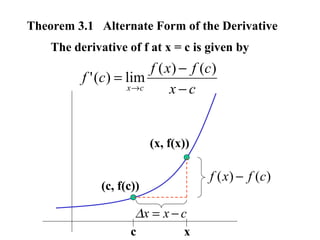
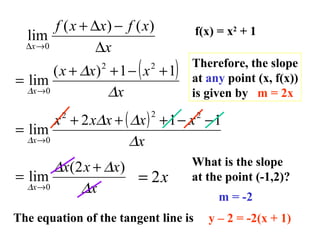
1) The document discusses the tangent line problem, one of the major problems that led to the development of calculus. It involves finding the slope of a tangent line to a curve at a point. 2) The derivative of a function f(x) is defined as the limit of the difference quotient as Δx approaches 0. This limit used to define the slope of a tangent line also defines the fundamental operation of differentiation in calculus. 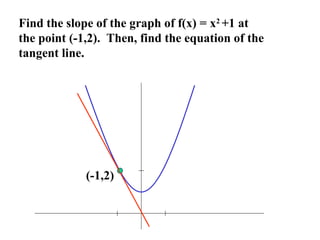3) A function is not differentiable at a point where its graph has a sharp turn, vertical tangent, or discontinuity, since the one-sided limits at that point would not be equal.

1. I’m going nuts
over derivatives!!!
2.1
The Derivative and the
Tangent Line Problem

2. Calculus grew out of 4 major problems that
European mathematicians were working on
in the seventeenth century.
1. The tangent line problem
2. The velocity and acceleration problem
3. The minimum and maximum problem
4. The area problem

3. The tangent line problem
(c, f(c))
secant line
f(c+ ) – f(c)x(c, f(c)) is the point of tangency and
is a second point on the graph of f.
)()( cfxcf −+ ∆
x∆
( ))(, xcfxc ∆+∆+

4. The slope between these two points is
cxc
cfxcf
m
−+
−+
=
∆
∆ )()(
sec
x
cfxcf
∆
∆ )()( −+
=
Definition of Tangent Line with Slope m
m
x
cfxcf
x
=
−+
→ ∆
∆
∆
)()(
lim
0

5. Find the slope of the graph of f(x) = x2
+1 at
the point (-1,2). Then, find the equation of the
tangent line.
(-1,2)

6. x
xfxxf
x ∆
−∆+
→∆
)()(
lim
0
( )
x
xxx
x ∆
∆
∆
11)(
lim
22
0
+−++
=
→
( )
x
xxxxx
x ∆
∆∆
∆
112
lim
222
0
−−+++
=
→
x
xxx
x ∆
∆∆
∆
)2(
lim
0
+
=
→
x2=
Therefore, the slope
at any point (x, f(x))
is given by m = 2x
What is the slope
at the point (-1,2)?
m = -2
The equation of the tangent line is y – 2 = -2(x + 1)
f(x) = x2
+ 1

7. The limit used to define the slope of a tangent
line is also used to define one of the two funda-
mental operations of calculus --- differentiation
Definition of the Derivative of a Function
x
xfxxf
xf
x ∆
∆
∆
)()(
lim)('
0
−+
=
→
f’(x) is read “f prime of x”
Other notations besides f’(x) include:
][)],([,', yDxf
dx
d
y
dx
dy
x

8. Find f’(x) for f(x) = and use the result to find
the slope of the graph of f at the points (1,1) &
(4,2). What happens at the point (0,0)?
,x
x
xfxxf
xf
x ∆
∆
∆
)()(
lim)('
0
−+
=
→
x
xxx
xf
x ∆
∆
∆
−+
=
→0
lim)(' 







++
++
⋅
xxx
xxx
∆
∆
( )xxxx
xxx
x ++
−+
=
→ ∆∆
∆
∆
)(
lim
0 ( )xxxx
xxx
x ++
−+
=
→ ∆∆
∆
∆ 0
lim
1
( )xxxx ++
=
→ ∆∆
1
lim
0 x2
1
=

9. x
mxf
2
1
)(' ==
Therefore, at the point (1,1), the
slope is ½, and at the point (4,2),
the slope is ¼.
What happens at the point (0,0)?
The slope is undefined, since it produces division
by zero.
2
1
=m
4
1
=m
1 2 3 4

10. Find the derivative with respect to t for the
function .
2
t
y =
t
tfttf
dx
dy
t ∆
∆
∆
)()(
lim
0
−+
=
→
t
ttt
t ∆
∆
∆
22
lim
0
−
+=
→
1
)(
)(22
lim
0 t
ttt
ttt
t ∆
∆
∆
∆
+
+−
=
→
tttt
ttt
t ∆∆
∆
∆
1
)(
222
lim
0
⋅
+
−−
=
→
2
2
t
−=

11. Theorem 3.1 Alternate Form of the Derivative
The derivative of f at x = c is given by
cx
cfxf
cf
cx −
−
=
→
)()(
lim)('
(c, f(c))
)()( cfxf −
cxx −=∆
c x
(x, f(x))

12. Derivative from the left and from the right.
cx
cfxf
cx −
−
−
→
)()(
lim
cx
cfxf
cx −
−
+
→
)()(
lim
Example of a point that is not differentiable.
2)( −= xxf is continuous at x = 2 but let’s
look at it’s one sided limits.
=
−
−
−
→ 2
)2()(
lim
2 x
fxf
x
=
−
−−
−
→ 2
02
lim
2 x
x
x
-1
=
−
−
+
→ 2
)2()(
lim
2 x
fxf
x
=
−
−−
+
→ 2
02
lim
2 x
x
x
1

13. The 1-sided limits are not equal.
∴, x is not differentiable at x = 2. Also, the
graph of f does not have a tangent line at the
point (2, 0).
A function is not differentiable at a point at
which its graph has a sharp turn or a vertical
tangent line(y = x1/3
or y = absolute value of x).
Differentiability can also be destroyed by
a discontinuity ( y = the greatest integer of x).