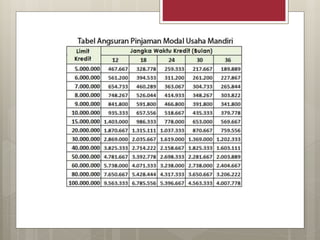
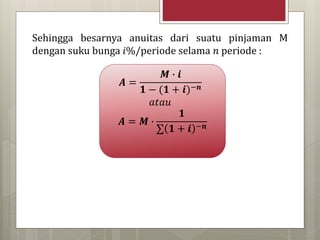
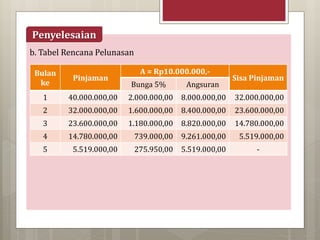
Dokumen tersebut membahas tentang konsep anuitas dalam matematika keuangan. Anuitas adalah pembayaran pinjaman yang sama besar yang dibayarkan setiap periode dan terdiri atas bunga dan angsuran. Diberikan rumus untuk menghitung besaran anuitas, contoh perhitungan, serta tabel rencana pelunasan untuk pinjaman yang akan dilunasi dengan sistem anuitas.

1. Anuitas
MATEMATIKA KEUANGAN

2. Tanpa kita sadari, kita sebenarnya sering
bersinggungan dengan konsep anuitas dalam kehidupan
sehari-hari. Misalnya, ketika kita membayar kredit
mobil, kredit rumah, dan membayar uang sewa rumah.
Ketika kita menabung secara rutin dalam jumlah yang
tetap setiap periode, kita juga tengah menerapkan
anuitas itu. Lantas, apakah anuitas itu?

4. Definisi Anuitas
Anuitas adalah sejumlah pembayaran pinjaman yang
sama besarnya yang dibayarkan setiap jangka waktu
tertentu, dan terdiri atas bagian bunga dan bagian
angsuran.
untuk 𝑛 bilangan asli.
Karena besarnya anuitas selalu tetap, maka yang
berubah adalah angsuran dan bunga.
𝑨𝒏𝒖𝒊𝒕𝒂𝒔 = 𝑨𝒏𝒈𝒔𝒖𝒓𝒂𝒏 + 𝑩𝒖𝒏𝒈𝒂
atau
𝑨 = 𝒂 𝒏 + 𝒃 𝒏

5. Jika suatu pinjaman sebesar 𝑀 dilunasi dengan sistem
anuitas selama 𝑛 periode dengan suku bunga
𝑖%/periode, setiap anuitasnya sama besar maka :
𝐴 𝑛+1 = 𝐴 𝑛
𝑎 𝑛+1 + 𝑏 𝑛+1 = 𝑎 𝑛 + 𝑏 𝑛
𝑎 𝑛+1 + 𝑖 ∙ 𝑀 𝑛+1 = 𝑎 𝑛 + 𝑖 ∙ 𝑀 𝑛
𝑎 𝑛+1 = 𝑎 𝑛 + 𝑖 ∙ 𝑀 𝑛 − 𝑀 𝑛+1
𝑎 𝑛+1 = 𝑎 𝑛 + 𝑖 ∙ 𝑎 𝑛
𝑎 𝑛+1 = 𝑎 𝑛 1 + 𝑖
Sehingga diperoleh
𝑎2 = 𝑎1 1 + 𝑖 ,
𝑎3 = 𝑎2 1 + 𝑖 = 𝑎1 1 + 𝑖 2,
𝑎4 = 𝑎3 1 + 𝑖 = 𝑎1 1 + 𝑖 3, dst.

6. Sehingga dapat diperoleh rumus angsuran ke-𝑛 sebagai
berikut :
𝒂 𝒏 = 𝒂 𝟏(𝟏 + 𝒊) 𝒏−𝟏
atau
𝒂 𝒏 = 𝒂 𝒌(𝟏 + 𝒊) 𝒏−𝒌

7. Besarnya pinjaman = jumlah semua angsuran
𝑀 = 𝑎1 + 𝑎2 + 𝑎3 + ⋯ + 𝑎 𝑛
𝑀 = 𝑎1 + 𝑎1 1 + 𝑖 + 𝑎1 1 + 𝑖 2 + ⋯ + 𝑎1(1 + 𝑖) 𝑛−1
𝑀 =
𝑎1 (1 + 𝑖) 𝑛−1
1 + 𝑖 − 1
𝑀 =
𝑎1 (1 + 𝑖) 𝑛−1
𝑖
𝑎1 =
𝑀 ∙ 𝑖
(1 + 𝑖) 𝑛−1
𝐴 − 𝑏1 =
𝑀 ∙ 𝑖
(1 + 𝑖) 𝑛−1
𝐴 − 𝑀 ∙ 𝑖 =
𝑀 ∙ 𝑖
(1 + 𝑖) 𝑛−1

8. 𝐴 = 𝑀 ∙ 𝑖 +
𝑀 ∙ 𝑖
(1 + 𝑖) 𝑛−1
𝐴 =
𝑀 ∙ 𝑖 ∙ 1 + 𝑖 𝑛 − 1 + 𝑀 ∙ 𝑖
(1 + 𝑖) 𝑛−1
𝐴 =
𝑀 ∙ 𝑖 ∙ 1 + 𝑖 𝑛
− 1 + 1
(1 + 𝑖) 𝑛−1
𝐴 =
𝑀 ∙ 𝑖 ∙ 1 + 𝑖 𝑛
(1 + 𝑖) 𝑛−1
𝐴 =
𝑀 ∙ 𝑖
1 − (1 + 𝑖) 𝑛−1

9. Sehingga besarnya anuitas dari suatu pinjaman M
dengan suku bunga 𝑖%/periode selama 𝑛 periode :
𝑨 =
𝑴 ∙ 𝒊
𝟏 − (𝟏 + 𝒊)−𝒏
𝑎𝑡𝑎𝑢
𝑨 = 𝑴 ∙
𝟏
∑ 𝟏 + 𝒊 −𝒏

10. Tentukan nilai anuitas dari suatu pinjaman sebesar Rp5.000.000,00
selama 2 tahun dengan suku bunga 2%/bulan!
Contoh
𝑀 = Rp5.000.000,00
𝑖 = 2%/bulan
𝑛 = 2 tahun = 24 bulan
𝐴 =
𝑀 ∙ 𝑖
1 − (1 + 𝑖)−𝑛
=
5.000.000 ∙ 0.02
1 − (1 + 0.02)−24
= 264.340,47
Jadi, nilai anuitas adalah Rp264.340,47
Penyelesaian

11. Suatu pinjaman Rp2.600.000,00 akan dilunasi dengan anuitas
bulanan Rp 250.000,00. Jika suku bunga 4%/bulan, tentukan:
a. Besarnya bunga pertama dan angsuran pertama!
b. Besarnya angsuran ke-5!
c. Besarnya bunga ke-8!
Contoh
𝑀 = Rp2.600.000,00
A = Rp250.000,00 perbulan
𝑖 = 4%/bulan
a. Bunga pertama :
𝑏1 = 𝑀 ∙ 𝑖 = 2.600.000 × 0.04 = 104.000
Angsuran pertama :
𝑎1 = 𝐴 − 𝑏1 = 250.000 − 104.000 = 146.000
Penyelesaian

12. 𝑀 = Rp2.600.000,00
A = Rp250.000,00 perbulan
𝑖 = 4%/bulan
𝑎1 = 146.000
b. Angsuran ke-5 :
𝑎5 = 𝑎1(1 + 𝑖)4= 146.000(1 + 0.04)4= 170.799,35
c. Bunga ke-8 :
𝑎8 = 𝑎1(1 + 𝑖)7= 146.000(1 + 0.04)7= 192.126,04
𝐴 = 𝑎8 + 𝑏8
𝑏8 = 250.000 − 192.126,04
𝑏8 = 57.87396
Penyelesaian

13. Tabel Rencana Pelunasan Anuitas

14. Utang sebesar Rp40.00.000,00 akan dilunasi dengan anuitas
sebesar Rp10.000.000,00 per bulan., dengan besarnya suku bunga
5%.
Buatlah : a. Rencana pelunasannya
b. Tabel rencana pelunasannya
Contoh
M = Rp40.000.000,00 𝑖 = 5%
A = Rp10.000.000,00
a. Rencana pelunasan
Bulan ke-1 :
𝑏1 = 0,05 × 𝑅𝑝40.000.000,00 = 𝑅𝑝2.000.000,00
𝑎1 = 𝐴 − 𝑏1 = 𝑅𝑝10.000.000,00 − 𝑅𝑝2.000.000,00
= 𝑅𝑝8.000.000,00
Sisa utang = Rp40.000.000,00 – Rp8.000.000,00
= Rp32.000.000,00
Penyelesaian

15. Bulan ke-2 :
𝑀2 = Rp32.000.000,00
𝑏2 = 0,05 × 𝑅𝑝32.000.000,00 = 𝑅𝑝1.600.000,00
𝑎2 = 𝐴 − 𝑏1 = 𝑅𝑝10.000.000,00 − 𝑅𝑝1.600.000,00
= 𝑅𝑝8.400.000,00
Sisa utang = Rp32.000.000,00 – Rp 8.400.000,00
= Rp23.600.000,00
Bulan ke-3 :
𝑀3 = Rp23.600.000,00
𝑏3 = 0,05 × 𝑅𝑝23.600.000,00 = 𝑅𝑝1.180.000,00
𝑎3 = 𝐴 − 𝑏1 = 𝑅𝑝10.000.000,00 − 𝑅𝑝1.180.000,00
= 𝑅𝑝8.820.000,00
Sisa utang = Rp23.600.000,00 – Rp 8.820.000,00
= Rp14.780.000,00
Penyelesaian

16. Bulan ke-4 :
𝑀4 = Rp14.780.000,00
𝑏4 = 0,05 × 𝑅𝑝14.780.000,00 = 𝑅𝑝739.000,00
𝑎4 = 𝐴 − 𝑏1 = 𝑅𝑝10.000.000,00 − 𝑅𝑝739.000,00
= 𝑅𝑝9.261.000,00
Sisa utang = Rp14.780.000,00 – Rp9.261.000,00
= Rp5.519.000,00
Bulan ke-5 :
𝑀5 = Rp5.519.000,00
𝑏1 = 0,05 × 𝑅𝑝5.519.000,00 = 𝑅𝑝275.950,00
Penyelesaian

17. b. Tabel Rencana Pelunasan
Penyelesaian
Bulan
ke
Pinjaman
A = Rp10.000.000,-
Sisa Pinjaman
Bunga 5% Angsuran
1 40.000.000,00 2.000.000,00 8.000.000,00 32.000.000,00
2 32.000.000,00 1.600.000,00 8.400.000,00 23.600.000,00
3 23.600.000,00 1.180.000,00 8.820.000,00 14.780.000,00
4 14.780.000,00 739.000,00 9.261.000,00 5.519.000,00
5 5.519.000,00 275.950,00 5.519.000,00 -