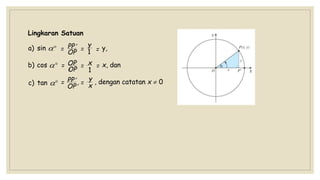
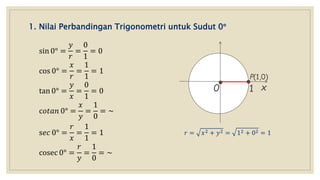
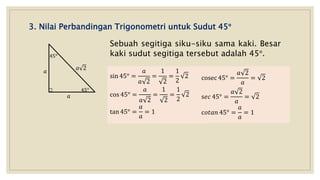
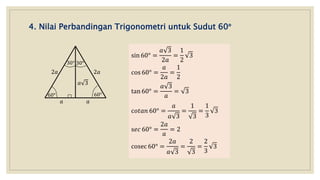
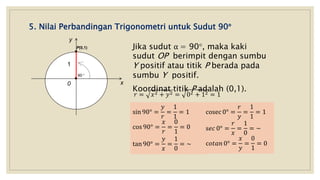
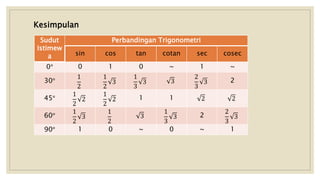
Dokumen ini membahas nilai perbandingan trigonometri untuk sudut istimewa seperti 0°, 30°, 45°, 60°, dan 90°, serta cara menghitungnya dengan berbagai metode. Selain itu, terdapat contoh perhitungan trigonometri yang melibatkan segitiga dan aplikasi dalam situasi sehari-hari, seperti mengukur tinggi pohon menggunakan sudut elevasi. Kesimpulannya, dokumen ini memberikan panduan komprehensif tentang dasar-dasar trigonometri yang diperlukan untuk siswa SMA kelas X.

1. TRIGONOMETRI
MATEMATIKA WAJIB SMA KELAS X

2. C. Nilai Perbandingan Trigonometri untuk Sudut Istimewa
Sudut istimewa adalah sudut dimana nilai
perbandingan trigonometrinya dapat ditentukan secara
langsung tanpa menggunakan daftar trigonometri atau
kalkulator.
Sudut-sudut yang dimaksud adalah susdut-sudut yang
besarnya 0°, 30°, 45°, 60°, dan 90°.

3. Lingkaran Satuan
a) sin 
b) cos 
c) tan 
=
=
=
PP
OP
OP
OP
OP
PP
y,
, dengan catatan x  0
1
y
1
x
y
x
=
=
=
=
= x, dan




4. 1. Nilai Perbandingan Trigonometri untuk Sudut 0°
x

0
P(1,0)
1
sin 0° =
𝑦
𝑟
=
0
1
= 0
cos 0° =
𝑥
𝑟
=
1
1
= 1
tan 0° =
𝑦
𝑥
=
0
1
= 0
c𝑜𝑡𝑎𝑛 0° =
𝑥
𝑦
=
1
0
= ~
s𝑒𝑐 0° =
𝑟
𝑥
=
1
1
= 1
cosec 0° =
𝑟
𝑦
=
1
0
= ~
𝑟 = 𝑥2 + 𝑦2 = 12 + 02 = 1

5. 2. Nilai Perbandingan Trigonometri untuk Sudut 30°
Sebuah segitiga sama sisi dengan panjang masing-
masing rusuk 2a. Besar masing-masing sudut
segitiga tersebut adalah 60°. Dari segitiga sama sisi
tersebut kita buat segitiga siku-siku dengan
menarik garis tinggi dari puncak segitiga tersebut.
Sehingga tinggi segitiga :
𝑡 = 2𝑎 2 − 𝑎 2 = 4𝑎2 − 𝑎2 = 3𝑎2 = 𝑎 360° 60°
30° 30°
2𝑎
𝑎 𝑎
2𝑎
sin 30° =
𝑎
2𝑎
=
1
2
cos 30° =
𝑎 3
2𝑎
=
1
2
3
tan 30° =
𝑎
𝑎 3
=
1
3
=
1
3
3
cosec 30° =
2𝑎
𝑎
= 2
s𝑒𝑐 30° =
2𝑎
𝑎 3
=
2
3
=
2
3
3
c𝑜𝑡𝑎𝑛 30° =
𝑎 3
𝑎
= 3

6. 3. Nilai Perbandingan Trigonometri untuk Sudut 45°
Sebuah segitiga siku-siku sama kaki. Besar
kaki sudut segitiga tersebut adalah 45°.
sin 45° =
𝑎
𝑎 2
=
1
2
=
1
2
2
cos 45° =
𝑎
𝑎 2
=
1
2
=
1
2
2
tan 45° =
𝑎
𝑎
= 1
cosec 45° =
𝑎 2
𝑎
= 2
s𝑒𝑐 45° =
𝑎 2
𝑎
= 2
c𝑜𝑡𝑎𝑛 45° =
𝑎
𝑎
= 1
45°
45°
𝑎
𝑎
𝑎 2

7. 4. Nilai Perbandingan Trigonometri untuk Sudut 60°
60° 60°
30° 30°
2𝑎
𝑎 𝑎
2𝑎
sin 60° =
𝑎 3
2𝑎
=
1
2
3
cos 60° =
𝑎
2𝑎
=
1
2
tan 60° =
𝑎 3
𝑎
= 3
c𝑜𝑡𝑎𝑛 60° =
𝑎
𝑎 3
=
1
3
=
1
3
3
s𝑒𝑐 60° =
2𝑎
𝑎
= 2
cosec 60° =
2𝑎
𝑎 3
=
2
3
=
2
3
3
𝑎 3

8. 5. Nilai Perbandingan Trigonometri untuk Sudut 90°
x
y

1
0
90
P(0,1)

Jika sudut α = 90, maka kaki
sudut OP berimpit dengan sumbu
Y positif atau titik P berada pada
sumbu Y positif.
Koordinat titik P adalah (0,1).
𝑟 = 𝑥2 + 𝑦2 = 02 + 12 = 1
sin 90° =
𝑦
𝑟
=
1
1
= 1
cos 90° =
𝑥
𝑟
=
0
1
= 0
tan 90° =
𝑦
𝑥
=
1
0
= ~
cosec 0° =
𝑟
𝑦
=
1
1
= 1
s𝑒𝑐 0° =
𝑟
𝑥
=
1
0
= ~
c𝑜𝑡𝑎𝑛 0° =
𝑥
𝑦
=
0
1
= 0

9. Kesimpulan
Sudut
Istimew
a
Perbandingan Trigonometri
sin cos tan cotan sec cosec
0° 0 1 0 ~ 1 ~
30°
1
2
1
2
3
1
3
3 3
2
3
3 2
45°
1
2
2
1
2
2 1 1 2 2
60°
1
2
3
1
2
3
1
3
3 2
2
3
3
90° 1 0 ~ 0 ~ 1

10. Hitunglah :
a. sin 30° + tan 45°
b. cos2 30° + tan2 45° − cosec2 60°
c.
sin 60°×cos 60°×tan 60°
sin 45°×tan 45°×cos 45°
Conto
h

11. a. sin 30° + tan 45° =
1
2
+ 1 = 1
1
2
b. cos2 30° + tan2 45° − cosec2 60° =
1
2
2
+ 12 −
2
3
3
2
=
1
4
+ 1 −
4
3
=
3 + 12 − 16
12
= −
1
12
Penyelesaia
n

12. c.
sin 60° × cos 60° × tan 60°
sin 45° × tan 45° × cos 45°
=
1
2
3 ×
1
2
× 3
1
2
2 ×1 ×
1
2
2
=
3
2
Penyelesaia
n

13. Tentukan nilai a pada gambar di bawah ini.
Conto
h
Y
X P
45°60°
Q 𝑎
24 cm

14.  Perhatikan segitiga PXY
tan 45° =
𝑋𝑌
𝑋𝑃
⟺ 1 =
𝑋𝑌
24
⟺ 𝑋𝑌 = 24
 Perhatikan segitiga QXY
tan 60° =
𝑋𝑌
𝑋𝑄
⟺ 3 =
24
𝑋𝑄
⟺ 𝑋𝑄 =
24
3
= 8 3
Penyelesaia
n
Y
X P
45°
24 cm
Y
X
60°
Q
𝑃𝑄 = 𝑃𝑋 − 𝑄𝑋
= 24 − 8 3
= 8 3 − 3
Jadi, nilai a adalah 8 3 − 3
cm

15. Seorang pengamat melihat puncak pohon dengan sudut elevasi
30°. Jika jarak antara pengamat dan pohon yang dilihatnya adalah
50 m, maka tinggi pohon tersebut adalah …
Conto
h
Misalkan tinggi pohon = t
tan 30° =
𝑡
50
⟺
1
3
3 =
𝑡
50
⟺ 𝑡 = 50 ∙
1
3
3 =
50
3
3
Jadi, tinggi pohon adalah
50
3
3 m.
Penyelesaia
n
30°
50 m
t = ?