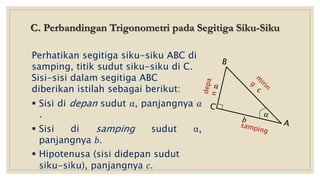
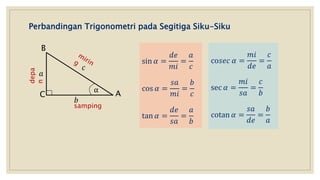
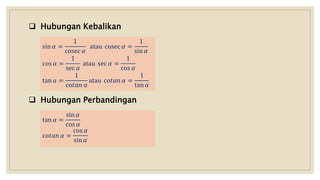
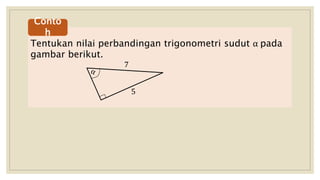
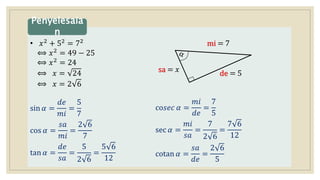
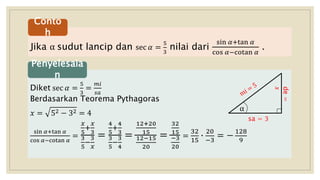
Dokumen menjelaskan perbandingan trigonometri pada segitiga siku-siku dan hubungannya. Definisi fungsi trigonometri seperti sin, cos, tan diberikan berdasarkan sisi-sisi segitiga. Contoh soal dan penyelesaiannya juga ditampilkan untuk mendemonstrasikan penggunaan perbandingan trigonometri dalam menentukan nilai sudut tidak diketahui.

1. TRIGONOMETRI
MATEMATIKA WAJIB SMA KELAS X

2. C. Perbandingan Trigonometri pada Segitiga Siku-Siku
Perhatikan segitiga siku-siku ABC di
samping, titik sudut siku-siku di C.
Sisi-sisi dalam segitiga ABC
diberikan istilah sebagai berikut:
 Sisi di depan sudut α, panjangnya 𝑎
.
 Sisi di samping sudut α,
panjangnya 𝑏.
 Hipotenusa (sisi didepan sudut
siku-siku), panjangnya 𝑐.

3. Perbandingan Trigonometri pada Segitiga Siku-Siku
A
B
C
𝑎
𝑏
𝑐
α
depa
n
samping
sin 𝛼 =
𝑑𝑒
𝑚𝑖
=
𝑎
𝑐
cos 𝛼 =
𝑠𝑎
𝑚𝑖
=
𝑏
𝑐
tan 𝛼 =
𝑑𝑒
𝑠𝑎
=
𝑎
𝑏
co𝑠𝑒𝑐 𝛼 =
𝑚𝑖
𝑑𝑒
=
𝑐
𝑎
sec 𝛼 =
𝑚𝑖
𝑠𝑎
=
𝑐
𝑏
cotan 𝛼 =
𝑠𝑎
𝑑𝑒
=
𝑏
𝑎

4.  Hubungan Kebalikan
sin 𝛼 =
1
cosec 𝛼
atau cosec 𝛼 =
1
sin 𝛼
cos 𝛼 =
1
sec 𝛼
atau sec 𝛼 =
1
cos 𝛼
tan 𝛼 =
1
co𝑡𝑎𝑛 𝛼
atau co𝑡𝑎𝑛 𝛼 =
1
tan 𝛼
 Hubungan Perbandingan
tan 𝛼 =
sin 𝛼
cos 𝛼
co𝑡𝑎𝑛 𝛼 =
cos 𝛼
sin 𝛼

5. Tentukan nilai perbandingan trigonometri sudut α pada
gambar berikut.
Conto
h
7

6. • 𝑥2 + 52 = 72
⟺ 𝑥2 = 49 − 25
⟺ 𝑥2
= 24
⟺ 𝑥 = 24
⟺ 𝑥 = 2 6
sin 𝛼 =
𝑑𝑒
𝑚𝑖
=
5
7
cos 𝛼 =
𝑠𝑎
𝑚𝑖
=
2 6
7
tan 𝛼 =
𝑑𝑒
𝑠𝑎
=
5
2 6
=
5 6
12
Penyelesaia
n
de = 5
mi = 7
sa = 𝑥
co𝑠𝑒𝑐 𝛼 =
𝑚𝑖
𝑑𝑒
=
7
5
sec 𝛼 =
𝑚𝑖
𝑠𝑎
=
7
2 6
=
7 6
12
cotan 𝛼 =
𝑠𝑎
𝑑𝑒
=
2 6
5

7. Tentukan nilai perbandingan trigonometri sudut α yang
lain jika diketahui sin 𝛼 =
2
3
.
Conto
h
sin 𝛼 =
𝑑𝑒
𝑚𝑖
=
2
3
cos 𝛼 =
𝑠𝑎
𝑚𝑖
=
5
3
tan 𝛼 =
𝑑𝑒
𝑠𝑎
=
2
5
=
2 5
5
Penyelesaia
n
de=
2
α
sa = 32 − 22 = 5
cosec 𝛼 =
𝑚𝑖
𝑑𝑒
=
3
2
sec 𝛼 =
𝑚𝑖
𝑠𝑎
=
3
5
=
3 5
5
cotan 𝛼 =
𝑠𝑎
𝑑𝑒
=
5
2

8. Jika α sudut lancip dan sec 𝛼 =
5
3
nilai dari
sin 𝛼+tan 𝛼
cos 𝛼−cotan 𝛼
.
Conto
h
Diket sec 𝛼 =
5
3
=
𝑚𝑖
𝑠𝑎
Berdasarkan Teorema Pythagoras
𝑥 = 52 − 32 = 4
sin 𝛼+tan 𝛼
cos 𝛼−cotan 𝛼
=
𝑥
5
+
𝑥
3
3
5
−
3
𝑥
=
4
5
+
4
3
3
5
−
3
4
=
12+20
15
12−15
20
=
32
15
−3
20
=
32
15
∙
20
−3
= −
128
9
Penyelesaia
n
de=
𝑥
α
sa = 3