Downloaded 1,470 times
Uploaded byLia Oktafiani
Matematika Keuangan - Anuitas dan Rente
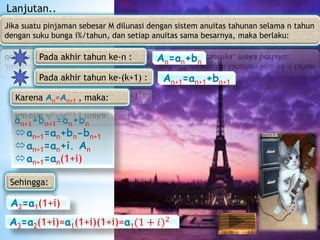
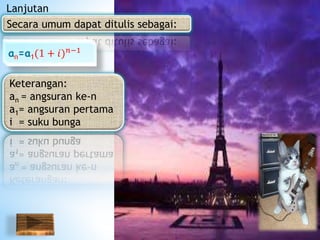
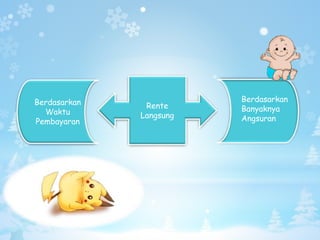
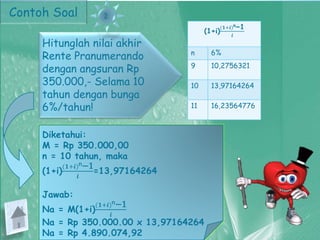
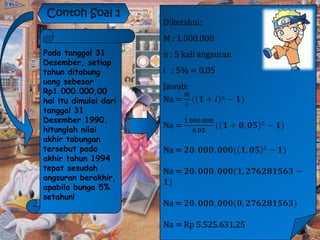
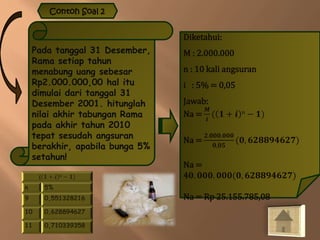
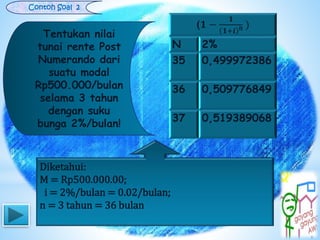
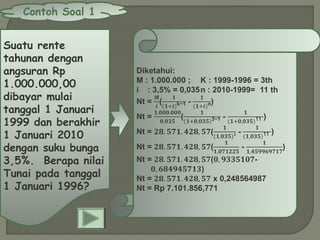
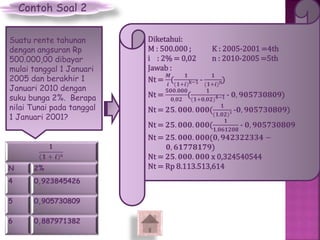
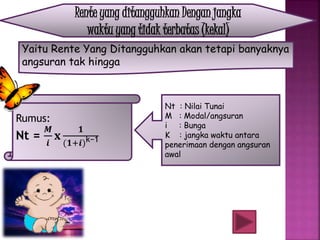
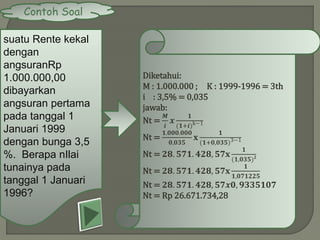
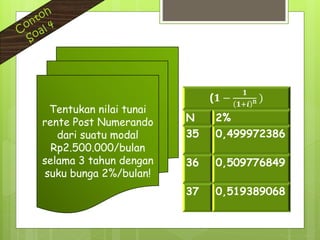
Dokumen ini membahas konsep anuitas, nilai tunai, dan metode perhitungan bunga dalam konteks keuangan. Terdapat contoh soal yang menjelaskan perhitungan anuitas, nilai akhir, dan nilai tunai dari pembayaran angsuran, baik pranumerando maupun postnumerando, serta rente kekal. Semua rumus dan contoh ini bertujuan untuk memberikan pemahaman praktis mengenai pengelolaan keuangan dan pembiayaan.
More Related Content
Similar to Matematika Keuangan - Anuitas dan Rente
![Modul Ajar KBC Fikih Kelas 2 MI [MODULKELAS.COM]](https://cdn.slidesharecdn.com/ss_thumbnails/modulajarkbcfikihkelas2mimodulkelas-260129153051-998e7c8f-thumbnail.jpg?width=640&height=640&fit=bounds)
Matematika Keuangan - Anuitas dan Rente
- 1. ACHMAD RIZWAN KURNIAWAN(02) GIOVANI ARSITA LUTHFIA (19) LIA OKTAFIANI (27) SUCI KUSTIAWATI (35) ULFIE BAVARIANTI MARLA (36)
- 3. Anuitas adalah sejumlah pembayaranyang sama besarnya, yang dibayarkan setiap akhir jangka waktu, dan terdiri atas bagian bunga dan bagian angsuran.
- 4. Anuitas = Bunga+ Angsuran Jika besarnya bunga adalah A, angsuran periode ke-n dinyatakan dengan an, dan bunga periode ke-n adalah bn, maka diperoleh hubungan : A=an+bn Rumus dengan n = 1, 2, 3, ...
- 5. Jika suatu pinjamansebesar M dilunasi dengan sistem anuitas tahunan selama n tahun dengan suku bunga i%/tahun, dan setiap anuitas sama besarnya, maka berlaku: an+1+bn+1=an+bn an+1=an+bn-bn+1 an+1=an+i. An an+1=an(1+i) An=an+bn Lanjutan.. Pada akhir tahun ke-n : Pada akhir tahun ke-(k+1) : An+1=an+1+bn+1 Karena An=An+1 , maka: Sehingga: A2=a1(1+i) A3=a2(1+i)=a1(1+i)(1+i)=a1(1 + 𝑖)2
- 6. Secara umum dapatditulis sebagai: an=a1(1 + 𝑖) 𝑛−1 Lanjutan Keterangan: an = angsuran ke-n a1= angsuran pertama i = suku bunga
- 7. Contoh Soal Suatu pinjaman akandilunasi dengan anuitas tahunan. Tentukan besarnya anuitas jika besarnya angsuran ke-6 dan bunga ke-6 masing-masing adalah Rp215.000,00 dan Rp85.000,00! Jawab: a6 = Rp215.000,00 b6 = Rp85.000,00 A = a6 + b6 A = Rp215.000,00+Rp85.000,00 = Rp400.000,00
- 8.
- 9.
- 12.
- 13. Nilai Akhir RentePranumerando adalah jumlah nilai akhir dari semua pembayaran angsuran pranumerando, dihitung pada akhir jangka waktu pembayaran terakhir. Rumus : Na = M(1+i) (𝟏+𝒊)n−1 𝒊 Na : Nilai Akhir tiap angsuran M : angsuran/modal n : Banyaknya angsuran/jangka waktu i : Bunga
- 14. Contoh Soal Seorang karyawan setiap awalbulan menyimpan uang di bank sebesar Rp500.000,00. Bank memberikan bunga 1,5%/bulan selama 2 tahun. Tentukan simpanan karyawan selama 2 tahun! Diketahui: M = Rp 500.000,00 i =1,5%/bulan = 0,015/bulan n = 2 tahun = 24 bulan Jawab: Na = M(1+i) (𝟏+𝒊)n−1 𝒊 Na = Rp 500.000.00 (1+0,015) (𝟏+𝟎,𝟎𝟏𝟓) 𝟐𝟓𝟒−𝟏 𝟎,𝟎𝟏𝟓 Na = Rp 500.000.00 (1,015) (𝟏,𝟎𝟏𝟓) 𝟐𝟒−𝟏 𝟎,𝟎𝟏𝟓 Na = Rp 500.000.00 (1,015) 1,429502812−1 0,015 Na = Rp 500.000.00 (1,015) 0,429502812 0,015 Na = Rp 500.000.00 (1,015)28,6335208 Na = Rp 500.000.00 x 29,063023607 Na = Rp 14.531.511,80
- 15. Contoh Soal (1+i) (𝟏+𝒊)n−1 𝒊 n 6% 910,2756321 10 13,97164264 11 16,23564776 Hitunglah nilai akhir Rente Pranumerando dengan angsuran Rp 350.000,- Selama 10 tahun dengan bunga 6%/tahun! Diketahui: M = Rp 350.000,00 n = 10 tahun, maka (1+i) (𝟏+𝒊)n−1 𝒊 =13,97164264 Jawab: Na = M(1+i) (𝟏+𝒊)n−1 𝒊 Na = Rp 350.000.00 x 13,97164264 Na = Rp 4.890.074,92
- 16. Yaitu jumlah nilaitunai dari semua pembayaran angsuran Pranumerando yang dihitung pada permulaan jangka waktu pembayaran pertama. Rumus : Nt = M(1+i)(𝟏− 𝟏+𝒊 −n) 𝒊 Nt : Nilai Tunai M : angsuran/modal n : Banyaknya angsuran/jangka waktu i : Bunga
- 17. Tentukan nilai tunai rentePra numerando dari suatu angsuran Rp4.000.000,00 selama 20 tahun dengan suku bunga 9%/tahun! Diketahui: M = Rp4.000.000,00 i = 9%/tahun = 0.09/tahun n = 20 Tahun Jawab: Nt = M(1+i)(𝟏− 𝟏+𝒊 −n) 𝒊 Nt = 4.000.000(1+0,09)(𝟏− 𝟏+𝟎,𝟎𝟗 −20) 𝟎,𝟎𝟗 Nt = 4.000.000(1,09)(𝟏− 𝟏,𝟎𝟗 −20) 𝟎,𝟎𝟗 Nt = 4.000.000(1,09)(𝟏−𝟎,𝟏𝟕𝟖𝟒𝟑𝟎𝟖𝟖𝟗) 𝟎,𝟎𝟗 Nt = 4.000.000(1,09)(𝟎,𝟖𝟐𝟏𝟓𝟔𝟗𝟏𝟏) 𝟎,𝟎𝟗 Nt = 4.000.000 . (0,895510329) 𝟎,𝟎𝟗 Nt = 𝟑.𝟓𝟖𝟐.𝟎𝟒𝟏,𝟑𝟐 𝟎,𝟎𝟗 Nt = Rp 39.800.459,11
- 18. Contoh Soal (𝟏 −𝟏 + 𝒊 −n ) n 3% 6 0,162515743 7 0,186908488 8 0,210590765 Pada tiap permulaan tahun, Suci akan menerima uang dari Yayasan Harapan sebesar Rp 2.000.000,- . Kalau uang itu akan diterimanya 7 kali dengan bunga 3% setahun, banyaknya uang yang dapat diterima Suci pada permulaan tahun yang pertama sebagai ganti rente tersebut adalah? Diketahui: M = Rp2.000.000,00 i = 3%/tahun=0,03 n = 7 Tahun Jawab: Nt = M(1+i)(𝟏− 𝟏+𝐢 −n) 𝐢 Nt = 2.000.000(1+0,03).0,186908488 𝟎,𝟎𝟑 Nt = 2.000.000 x 0,192515742 𝟎,𝟎𝟑 Nt = 385.031,48 𝟎,𝟎𝟑 Nt = 𝟏𝟐. 𝟖𝟑𝟒. 𝟑𝟖𝟐, 𝟔𝟕
- 21. Nilai Akhir RentePostnumerando Yaitu jumlah nilai akhir dari semua pembayaran angsuran postnumerando dihitung pada akhir jangka waktu pembayaran terakhir. Rumus : Na = 𝑴 𝒊 ( 𝟏 + 𝒊 n − 𝟏) Na : Nilai akhir tiap angsuran M : angsuran/modal n : Banyaknya angsuran/jangka waktu i : Bunga
- 22. Contoh Soal 1 Padatanggal 31 Desember, setiap tahun ditabung uang sebesar Rp1.000.000,00 hal itu dimulai dari tanggal 31 Desember 1990. hitunglah nilai akhir tabungan tersebut pada akhir tahun 1994 tepat sesudah angsuran berakhir, apabila bunga 5% setahun! Diketahui: M : 1.000.000 n : 5 kali angsuran i : 5% = 0,05 Jawab: Na = 𝑴 𝒊 ( 𝟏 + 𝒊 n − 𝟏) Na = 𝟏.𝟎𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟓 ( 𝟏 + 𝟎, 𝟎𝟓 5 − 𝟏) Na = 𝟐𝟎. 𝟎𝟎𝟎. 𝟎𝟎𝟎( 𝟏, 𝟎𝟓 5 − 𝟏) Na = 𝟐𝟎. 𝟎𝟎𝟎. 𝟎𝟎𝟎(𝟏, 𝟐𝟕𝟔𝟐𝟖𝟏𝟓𝟔𝟑 − 𝟏) Na = 𝟐𝟎. 𝟎𝟎𝟎. 𝟎𝟎𝟎(𝟎, 𝟐𝟕𝟔𝟐𝟖𝟏𝟓𝟔𝟑) Na = Rp 5.525.631,25
- 23. Contoh Soal 2 Padatanggal 31 Desember, Rama setiap tahun menabung uang sebesar Rp2.000.000,00 hal itu dimulai dari tanggal 31 Desember 2001. hitunglah nilai akhir tabungan Rama pada akhir tahun 2010 tepat sesudah angsuran berakhir, apabila bunga 5% setahun! Diketahui: M : 2.000.000 n : 10 kali angsuran i : 5% = 0,05 Jawab: Na = 𝑴 𝒊 ( 𝟏 + 𝒊 n − 𝟏) Na = 𝟐.𝟎𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟓 (𝟎, 𝟔𝟐𝟖𝟖𝟗𝟒𝟔𝟐𝟕) Na = 4𝟎. 𝟎𝟎𝟎. 𝟎𝟎𝟎(𝟎, 𝟔𝟐𝟖𝟖𝟗𝟒𝟔𝟐𝟕) Na = Rp 25.155.785,08 ( 𝟏 + 𝒊 n − 𝟏) n 5% 9 0,551328216 10 0,628894627 11 0,710339358
- 24. Yaitu jumlah nilaitunai dari semua pembayaran angsuran postnumerando dihitung pada awal jangka waktu pembayaran pertama. Rumus : Nt = 𝑴 𝒊 (𝟏 − 𝟏 𝟏+𝒊 n ) Nt : Nilai Tunai tiap angsuran M : angsuran/modal n : Banyaknya angsuran/jangka waktu i : Bunga
- 25. Contoh Soal 1 Tentukannilai tunai rente Post Numerando dari suatu modal Rp300.000/bulan selama 2.5 tahun dengan suku bunga 1.5%/bulan! Diketahui: M = Rp300.000.00; i = 1.5%/bulan = 0.015/bulan; n = 2 tahun 6 bulan = 30 bulan Jawab: Nt = 𝑴 𝒊 (𝟏 − 𝟏 𝟏+𝒊 n ) Nt = 𝟑𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟏𝟓 (𝟏 − 𝟏 𝟏+𝟎,𝟎𝟏𝟓 30 ) Nt = 𝟐𝟎. 𝟎𝟎𝟎. 𝟎𝟎𝟎 (𝟏 − 𝟏 𝟏,𝟎𝟏𝟓 30 ) Nt = 𝟐𝟎. 𝟎𝟎𝟎. 𝟎𝟎𝟎 (𝟏 − 𝟏 𝟏,𝟓𝟔𝟑𝟎𝟖𝟎𝟐𝟐 ) Nt = 𝟐𝟎. 𝟎𝟎𝟎. 𝟎𝟎𝟎 (𝟏 − 𝟎, 𝟔𝟑𝟗𝟕𝟔𝟐𝟒𝟑) Nt = 𝟐𝟎. 𝟎𝟎𝟎. 𝟎𝟎𝟎 (𝟎, 𝟑𝟔𝟎𝟐𝟑𝟕𝟓𝟔𝟗) Nt = Rp 7.204.751,38
- 26. Contoh Soal 2 Diketahui: M= Rp500.000.00; i = 2%/bulan = 0.02/bulan; n = 3 tahun = 36 bulan Tentukan nilai tunai rente Post Numerando dari suatu modal Rp500.000/bulan selama 3 tahun dengan suku bunga 2%/bulan! (𝟏 − 𝟏 𝟏+𝒊 n ) N 2% 35 0,499972386 36 0,509776849 37 0,519389068
- 27. Jawab: Nt = 𝑴 𝒊 (𝟏 − 𝟏 𝟏+𝒊n ) Nt = 𝟓𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟐 (𝟎, 𝟓𝟎𝟗𝟕𝟕𝟔𝟖𝟒𝟗) Nt = 𝟐𝟓. 𝟎𝟎𝟎. 𝟎𝟎𝟎 (𝟎, 𝟓𝟎𝟗𝟕𝟕𝟔𝟖𝟒𝟗) Nt = Rp 12.744.421,23
- 28.
- 29. Rente Kekal Rente Kekalmerupakan Rente yang dibayarkan selama jangka waktu tak terbatas (n = ~). Maka dari hanya nilai tunainya saja yang dapat dihitung, sedangkan nilai akhirnya tidak dapat dihitung jumlahnya. 2
- 31. Rente Kekal Pranumerando Yaitujumlah nilai tunai dari semua pembayaran angsuran pranumerando kekal dihitung pada awal jangka waktu pembayaran pertama. Rumus: Nt = M + 𝑴 𝒊 Nt : Nilai Tunai M : Modal/angsuran i : Bunga RENTE KEKAL
- 32. Contoh Soal Sebuah yayasan mempunyaikewajiban membayar pajak kepada pemerintah melalui sebuah bank setiap awal tahunnya sebesar Rp50.000,- dan bunganya 8%. Yayasan tersebut ingin membayar kewajibannya sekaligus diawal pembayaran pertama. Berapa besar jumlah yang harus dibayar oleh yayasan tersebut! Jawab Diketahui : M = Rp50.000,- i = 8% = 0,08 Ditanyakan : Nt ? Jawab: Nt = M + 𝑴 𝒊 Nt = 50.000 + 𝟓𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟖 Nt =Rp 675.000,- Jadi, jumlah yang harus dibayar oleh yayasan adalah Rp 675.000,-
- 33. Rente Kekal Postnumerando Yaitujumlah nilai tunai dari semua pembayaran angsuran postnumerando kekal dihitung pada awal jangka waktu pembayaran pertama. Rumus: Nt = 𝑴 𝒊 Nt : Nilai Tunai M : Modal/angsuran i : Bunga RENTE KEKAL
- 34. Contoh Soal Sebuah yayasan mempunyaikewajiban membayar pajak kepada pemerintah melalui sebuah bank sebesar Rp115.000,- pertahun. Kewajiban tersebut harus dilakukan tiap akhir tahun. Jika yayasan ingin melakukan pelunasan sekaligus, berapa jumlah yang harus dibayar oleh yayasan tersebut! (bunga 6% pertahun) Jawab Diketahui : M = Rp115.000,- i = 6% = 0,06 Ditanyakan : Nt ? Jawab : Nt = 𝑴 𝒊 Nt = 𝟏𝟏𝟓.𝟎𝟎𝟎 𝟎,𝟎𝟔 Nt =Rp 1.916.666,67 Jadi, jumlah yang harus dibayar oleh yayasan adalah Rp 1.916.666,67
- 35.
- 36. Rente yang ditangguhkanDengan jangka waktu terbatas Yaitu Rente Yang Ditangguhkan dimana banyaknya angsuran diketahui Rumus: Nt = 𝑴 𝒊 ( 𝟏 (𝟏+𝒊)k−1 - 𝟏 (𝟏+𝒊)n) Nt : Nilai Tunai M : Modal/angsuran i : Bunga K : jangka waktu antara penerimaan dengan angsuran awal N : banyaknya angsuran/jangka waktu
- 37. Contoh Soal 1 Suaturente tahunan dengan angsuran Rp 1.000.000,00 dibayar mulai tanggal 1 Januari 1999 dan berakhir 1 Januari 2010 dengan suku bunga 3,5%. Berapa nilai Tunai pada tanggal 1 Januari 1996? Diketahui: M : 1.000.000 ; K : 1999-1996 = 3th i : 3,5% = 0,035n : 2010-1999= 11 th Nt = 𝑴 𝒊 ( 𝟏 (𝟏+𝒊)k−1 - 𝟏 (𝟏+𝒊)n) Nt = 𝟏.𝟎𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟑𝟓 ( 𝟏 (𝟏+𝟎,𝟎𝟑𝟓)3−1 - 𝟏 (𝟏+𝟎,𝟎𝟑𝟓)11 ) Nt = 𝟐𝟖. 𝟓𝟕𝟏. 𝟒𝟐𝟖, 𝟓𝟕( 𝟏 (𝟏,𝟎𝟑𝟓) 𝟐 - 𝟏 (𝟏,𝟎𝟑𝟓)11 ) Nt = 𝟐𝟖. 𝟓𝟕𝟏. 𝟒𝟐𝟖, 𝟓𝟕( 𝟏 𝟏,𝟎𝟕𝟏𝟐𝟐𝟓 - 𝟏 𝟏,𝟒𝟓𝟗𝟗𝟔𝟗𝟕𝟏𝟕 ) Nt = 𝟐𝟖. 𝟓𝟕𝟏. 𝟒𝟐𝟖, 𝟓𝟕(𝟎, 𝟗𝟑𝟑𝟓𝟏𝟎𝟕- 𝟎, 𝟔𝟖𝟒𝟗𝟒𝟓𝟕𝟏𝟑) Nt = 𝟐𝟖. 𝟓𝟕𝟏. 𝟒𝟐𝟖, 𝟓𝟕 x 0,248564987 Nt = Rp 7.101.856,771
- 38. Contoh Soal 2 𝟏 (𝟏+ 𝒊)n N 2% 4 0,923845426 5 0,905730809 6 0,887971382 Suatu rente tahunan dengan angsuran Rp 500.000,00 dibayar mulai tanggal 1 Januari 2005 dan berakhir 1 Januari 2010 dengan suku bunga 2%. Berapa nilai Tunai pada tanggal 1 Januari 2001? Diketahui: M : 500.000 ; K : 2005-2001 =4th i : 2% = 0,02 n : 2010-2005 =5th Jawab : Nt = 𝑴 𝒊 ( 𝟏 (𝟏+𝒊)k−1 - 𝟏 (𝟏+𝒊)n) Nt = 𝟓𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟐 ( 𝟏 (𝟏+𝟎,𝟎𝟐)4−1 - 𝟎, 𝟗𝟎𝟓𝟕𝟑𝟎𝟖𝟎𝟗) Nt = 𝟐𝟓. 𝟎𝟎𝟎. 𝟎𝟎𝟎( 𝟏 (𝟏,𝟎𝟐) 𝟑 -𝟎, 𝟗𝟎𝟓𝟕𝟑𝟎𝟖𝟎𝟗) Nt = 𝟐𝟓. 𝟎𝟎𝟎. 𝟎𝟎𝟎( 𝟏 𝟏,𝟎𝟔𝟏𝟐𝟎𝟖 - 𝟎, 𝟗𝟎𝟓𝟕𝟑𝟎𝟖𝟎𝟗 Nt = 𝟐𝟓. 𝟎𝟎𝟎. 𝟎𝟎𝟎(𝟎, 𝟗𝟒𝟐𝟑𝟐𝟐𝟑𝟑𝟒 − 𝟎, 𝟔𝟏𝟕𝟕𝟖𝟏𝟕𝟗) Nt = 𝟐𝟓. 𝟎𝟎𝟎. 𝟎𝟎𝟎 x 0,324540544 Nt = Rp 8.113.513,614
- 39. Rente yang ditangguhkanDengan jangka waktu yang tidak terbatas (kekal) Yaitu Rente Yang Ditangguhkan akan tetapi banyaknya angsuran tak hingga Rumus: Nt = 𝑴 𝒊 𝐱 𝟏 (𝟏+𝒊)k−1 Nt : Nilai Tunai M : Modal/angsuran i : Bunga K : jangka waktu antara penerimaan dengan angsuran awal
- 40. Contoh Soal suatu Rentekekal dengan angsuranRp 1.000.000,00 dibayarkan angsuran pertama pada tanggal 1 Januari 1999 dengan bunga 3,5 %. Berapa nIlai tunainya pada tanggal 1 Januari 1996? Diketahui: M : 1.000.000 ; K : 1999-1996 = 3th i : 3,5% = 0,035 jawab: Nt = 𝑴 𝒊 𝒙 𝟏 (𝟏+𝒊)k−1 Nt = 𝟏.𝟎𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟑𝟓 𝐱 𝟏 (𝟏+𝟎,𝟎𝟑𝟓)3−1 Nt = 𝟐𝟖. 𝟓𝟕𝟏. 𝟒𝟐𝟖, 𝟓𝟕𝐱 𝟏 (𝟏,𝟎𝟑𝟓) 𝟐 Nt = 𝟐𝟖. 𝟓𝟕𝟏. 𝟒𝟐𝟖, 𝟓𝟕𝐱 𝟏 𝟏,𝟎𝟕𝟏𝟐𝟐𝟓 Nt = 𝟐𝟖. 𝟓𝟕𝟏. 𝟒𝟐𝟖, 𝟓𝟕𝒙𝟎, 𝟗𝟑𝟑𝟓𝟏𝟎𝟕 Nt = Rp 26.671.734,28
- 42. Setiap awal tahunGio menyimpan uang di Bank ABC sebesar Rp.1.000.000,00. Jika bank memberikan bunga 6%/tahun, tentukan uang Gio setelah menabung 20 tahun!
- 43. Diketahui: M = Rp1.000.000,00 i =6%/tahun = 0,06/tahun n = 20 tahun Jawab: Na = M(1+i) (𝟏+𝒊)n−1 𝒊 Na = 1.000.000(1+0,06) (𝟏+𝟎,𝟎𝟔)20−1 𝟎,𝟎𝟔 Na = 1.000.000(1,06) (𝟏,𝟎𝟔)20−1 𝟎,𝟎𝟔 Na = 1.000.000(1,06) 𝟑,𝟐𝟎𝟕𝟏𝟑𝟓𝟒𝟕𝟐−1 𝟎,𝟎𝟔 Na = 1.000.000(1,06) 𝟑,𝟐𝟎𝟕𝟏𝟑𝟓𝟒𝟕𝟐−1 𝟎,𝟎𝟔 Na = 1.000.000(1,06) 𝟐,𝟐𝟎𝟕𝟏𝟑𝟓𝟒𝟕𝟐 𝟎,𝟎𝟔 Na = 1.000.000(1,06)x 3,67855912 Na = 1.000.000x3,899272667 Na = Rp 3.899.272,667
- 44. Rizwan akan mendapatbeasiswa pada setiap awal bulan dari LIA English Course sebesar Rp250.000,00 selama 3 tahun. Jika pemberian itu akan diberikan sekaligus di awal bulan pertama dengan dikenai bunga 2%/bulan, tentukan besarnya beasiswa total yang diterima Rizwan!
- 45. Diketahui: M = Rp250.000,00 i= 2%/bulan = 0,02/bulan n = 3 tahun = 36 bulan Jawab: Nt = M(1+i)(𝟏− 𝟏+𝒊 −n) 𝒊 Nt = 250.000(1+0,02)(𝟏− 𝟏+𝟎,𝟎𝟐 −36) 𝟎,𝟎𝟐 Nt = 250.000(1,02)(𝟏− 𝟏,𝟎𝟐 −36) 𝟎,𝟎𝟐 Nt = 255.000 𝒙 (𝟏−𝟎,𝟒𝟗𝟎𝟐𝟐𝟑𝟏𝟓) 𝟎,𝟎𝟐 Nt = 255.000 𝒙 0,509776849 𝟎,𝟎𝟐 Nt = 𝟏𝟐𝟗.𝟗𝟗𝟑,𝟎𝟗𝟔𝟓 𝟎,𝟎𝟐 Nt = Rp 6.499.654,825
- 46. Tiap akhir bulanYayasan Cinta Damai mendapatkan sumbangan dari Badan Perdamaian Dunia sebesar Rp5.000.000,00 selama 30 bulan berturut-turut. Jika sumbangan akan diberikan sekaligus dan di kenai bunga sebesar 2%/bulan, tentukan sumbangan total yg diterima yayasan!
- 47. Diketahui: M = Rp5.000.000,00 i = 2% / bulan = 0.02 / bulan n = 30 bulan Jawab: Na = 𝑴 𝒊 ( 𝟏 + 𝒊 n − 𝟏) Na = 𝟓.𝟎𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟐 ( 𝟏 + 𝟎, 𝟎𝟐 30 − 𝟏) Na = 𝟓.𝟎𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟐 ( 𝟏, 𝟎𝟐 30 − 𝟏) Na = 𝟓.𝟎𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟐 (𝟏, 𝟖𝟏𝟏𝟑𝟔𝟏𝟓𝟖𝟒 − 𝟏) Na = 𝟓.𝟎𝟎𝟎.𝟎𝟎𝟎 𝟎,𝟎𝟐 (𝟎, 𝟖𝟏𝟏𝟑𝟔𝟏𝟓𝟖𝟒) Na = 250.000.000 (𝟎, 𝟖𝟏𝟏𝟑𝟔𝟏𝟓𝟖𝟒) Na = 202.840.385
- 48. Tentukan nilai tunai rentePost Numerando dari suatu modal Rp2.500.000/bulan selama 3 tahun dengan suku bunga 2%/bulan! (𝟏 − 𝟏 𝟏+𝒊 n ) N 2% 35 0,499972386 36 0,509776849 37 0,519389068
- 49. Diketahui: M = Rp2.500.000.00; i= 2%/bulan = 0.02/bulan; n = 3 tahun = 36 bulan Jawab: Nt = 𝑀 𝑖 (1 − 1 1+𝑖 n ) Nt = 2.500.000 0,02 (0,509776849) Nt = 125.000.000 (0,509776849) Nt = Rp 245.205.329
- 50. Sebuah yayasan mempunyaikewajiban membayar pajak kepada pemerintah melalui sebuah bank sebesar Rp115.000,- pertahun. Kewajiban tersebut harus dilakukan tiap akhir tahun. Jika yayasan ingin melakukan pelunasan sekaligus, berapa jumlah yang harus dibayar oleh yayasan tersebut! (bunga 6% pertahun)
- 51. Diketahui : M= Rp115.000,- i = 6% = 0,06 Ditanyakan : Nt ? Jawab : Nt = 𝑀 𝑖 Nt = 115.000 0,06 Nt =Rp 1.916.666,67 Jadi, jumlah yang harus dibayar oleh yayasan adalah Rp 1.916.666,67