83662164 case-study-1

Module2:RootsofEquations
1
Homework Help
https://www.homeworkping.com/
Research Paper help
Online Tutoring
click here for freelancing tutoring sites
Chapter I
Introduction
Background
In the field of engineering electricity it is necessary to know the properties of
the materials to be used for a certain project of development or for a study to be
conducted. Failure to know the properties of the material to be made of, may lead to
the disappointment of the project. Thus, resistivity is one of the physical properties of
a material as of density, specific heat and many others. Resistivity is primarily defined
as the strength or capacity of the material to oppose the flow of an electric current.Any
object made of the same material has the common resistivity. When talking about
resistivity it doesn't matter how big or what shape the sample is, it is the object’s

2
resistance which depends on its length, cross sectional area, etc. The relationship
between the resistivity and resistance is shown by a formula,
where R is the resistance , r is the resistivity , L is the length of the material, and A is
the cross sectional area. Thus, resistivity related to resistance may be obtained
through mathematical process. Hence the SI unit for resistivity is ohm meter (Ω.m).
Another way of obtaining the resistivity (𝜌) of an object is based on its electron
content. It is defined that the resistivity( 𝜌 ) of a certain material is inversely
proportional to the electron charge (q), the electron density (n), and the electron
mobility (µ) measured in cm2.
Electron density is themeasure of the probability of an electron being present at
a specific location and the electron mobility is a quantity relating the drift velocity of
electrons to the applied electric field across a material. Electron density (n) is given by
the formula,
where N is determined as the doping density and ni as the intrinsic carrier density
measured in cm-3. And also the electron mobility ( 𝜇 ) is described by the final
𝑅 = 𝜌
𝐿
𝐴
(1)
𝜌 =
1
𝑞𝑛 𝜇
(2)
𝑛 =
1
2
( 𝑁+ √𝑁2 + 4𝑛𝑖
2 ) (2)

3
temperature and reference temperature T and 𝑇𝑜 respectively, and a reference electron
mobility ( 𝜇 𝑜). And it is given by a formula,
Engineering Problem Posed
The van der Waal equation of state for a vapor is
(𝑃 +
𝑎
𝑣2)( 𝑣 − 𝑏) = 𝑅𝑇
where P is the pressure (Pa = N/m2), v is the specific volume (m3/kg), the temperature
(K), R is the gas constant (J/kg-K), and a and b are empirical constants. Consider
water vapor, for which R=461.495J/kg-K, a=1703.28Pa-(m3/kg)3, and
b=0.00169099(m3/kg). Calculate the specific volume v for P = 10,000kPa and T =800K.
Mathematical Analysis
Different mathematical methods should be used to obtain the value in the given
problem. Thus, it needs to transform and express functions or working equations to
the form the problem requires.
The given equation can be rearranged by algebraic manipulation:
Engineering Problem Expressed Mathematically
Determine the specific volume (v) given 𝑅 = 461.495J/kg − K, 𝑎 = 1703.28Pa −
(m3/kg)3, 𝑏 = 0.00169099(m3/kg), 𝑃 = 10,000kPa,and 𝑇 = 800K.
𝜇 = 𝜇 𝑜(
𝑇
𝑇 𝑂
)−2.42 (3)
(3)

4
(𝑃 +
𝑎
𝑣2)( 𝑣 − 𝑏) = 𝑅𝑇
𝑃𝑣 − 𝑃𝑏 +
𝑎
𝑣
−
𝑎𝑏
𝑣2 = 𝑅𝑇
𝑃𝑣3 − 𝑃𝑏𝑣2 + 𝑎𝑣 − 𝑎𝑏 = 𝑅𝑇𝑣2
𝑃𝑣3 − ( 𝑃𝑏 + 𝑅𝑇) 𝑣2 + 𝑎𝑣 − 𝑎𝑏 = 0
𝑓( 𝑣) = 𝑃𝑣3 − ( 𝑃𝑏 + 𝑅𝑇) 𝑣2 + 𝑎𝑣 − 𝑎𝑏
Using the derived function, the value of (v) can be obtained with the aid of the different
mathematical numerical methods of solving problems.
Chapter II
Methods in Obtaining Roots of the Equation
Referring to Appendix A are the figures of the flowchart of the programs being
constructedfor each methods of obtaining root of an equation, it follows a subroutine
procedure. The program contains a main class obtaining the necessary methods
calling for inputs, and subclasses (Bisection, FalsePosition, FixedPoint Iteration,
NewtonRaphson, Secant, Brent) which leads to the computation of the root using any
method.
Bracketing Method

5
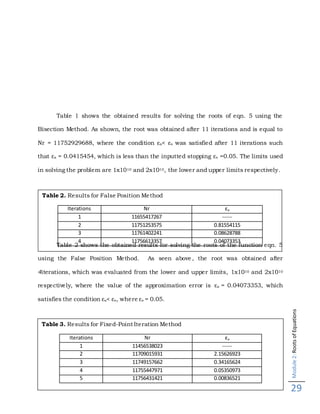
It comprises different methods which the roots may be found within the two
initial guesses which are typically changes the signs. The methods present here give
strategies which reducesthe width of the bracket until the root will be found.
Bisection Method
It is called the binary chopping or the Bolzano’s method. A Bracketing method
which finds root of a given continuous function over an interval 𝑥 𝑙 and𝑥 𝑢 such that
f(𝑥 𝑙) and f(𝑥 𝑢) will have an opposite signs that gives f(𝑥 𝑙) f(𝑥 𝑢) < 0. The method divides
the interval in two by computing the midpoint 𝑥 𝑟= (𝑥𝑙+𝑥 𝑢)/2 of the interval. Either f(𝑥 𝑙)
and f(𝑥 𝑟) or f(𝑥 𝑟) and f(𝑥 𝑢) will have opposite signs and it brackets a root, we must
select a subinterval within the interval and apply the same bisection step. There will
be a 50% of chance of getting a function equals to zero. If f(𝑥𝑙) f(𝑥 𝑟) < 0, then the
method sets equal 𝑥 𝑢 to𝑥 𝑟, and if f(𝑥 𝑢) f(𝑥 𝑟)< 0, then the method sets 𝑥 𝑙equal to 𝑥 𝑟. For
both cases, the new f(𝑥 𝑙) and f(𝑥 𝑢) will have opposite signs, so that the method is
applicable to this smaller interval.
The continuous function on the given interval [𝑥𝑙,𝑥 𝑢 ] and f(𝑥 𝑙) f(𝑥 𝑢) < 0 states
that the bisection converges to a root of the function and the true error is halved in
each step and the method converges linearly if f(𝑥 𝑙) and f(𝑥 𝑢) will have different signs.
This method gives only a range where the root exists and not the estimation where is
the roots location. The smallest bracket is where the root can be found. Its true error
of n steps can be solved by the equation;
𝜀 𝑡 =
𝑥 𝑙+𝑥 𝑢
2
(2.1)

6
False Position Method/Regula Falsi Method
It is also called the linear interpolation method. An alternative method based on
the graphical method. The false position method starts with a two points 𝑥𝑙 and 𝑥 𝑢
such that the functions f(𝑥𝑙) and f(( 𝑥 𝑢) will have an opposite signs then one of the end-
points will converges and the other will remain fixed for all the iterations function f a
root. It is given by the formula,
The root 𝑥 𝑟 is from the graphical representation of joining the function f(𝑥 𝑙) and
f(( 𝑥 𝑢) by a straight line and which the point that intersects the line and the axis is the
improve root. The value of the root replaces f(𝑥 𝑙) and f(( 𝑥 𝑢) with the same sign as f( 𝑥 𝑟)
so that the root is always at the interval of the two point 𝑥 𝑙 and 𝑥 𝑢.
The termination of the computation will be the same as the bisection method
and same as the algorithm, but the equation for finding 𝑥 𝑟 is used. The error of the
regula falsi is more efficient for root finding than the bisection since one of the points
will stay throughout the computation and the others converges quickly and makes the
approximate error conservative.
Modified False Position Method
It is the remedy of being one-sided of the false position method. It divides the
function value that was stuck. The algorithm implements the strategies on how the
𝑥 𝑟 = 𝑥 𝑢 −
𝑓( 𝑥 𝑢)(𝑥 𝑢−𝑥𝑙)
𝑓( 𝑥 𝑙)−𝑓(𝑥 𝑢)
(2.2)

7
counters are used to determine the root when the one is bound stays fixed for the two
iterations and through this, the function value is bound halved.
It is more than the bisection and the false position method for setting the
stopping criterion as 1.01% since it gives only 12 iterations compare with the 14 and
25 of the bisection and false position method.
Open Method
It composed of different methods that are based on the formulas that requires
only a single starting value of x or two starting values that do not necessarily bracket
the root. It may diverge or converges as the computation progresses.
Simple Fixed Point Method
It is also called the One-point iteration or the successive substitution method. It
rearranges the function f(x)=0 to x=g(x) It can be obtained by adding both sides a x of
the equation or by simply doing algebraic manipulation. The guess roots 𝑥 𝑖 can be
used to estimate as 𝑥𝑖+1 and can be expressed as 𝑥 𝑖+1=g(x).
The convergence or the divergence of this method can be depicted graphically through
its behavior and structure or it can also be predicted by separating the it into two
components parts and the x values obtained by the intersections are the roots of
the function f(x)=0. The two-curve method also shows the convergence and the

8
divergence of the simple fixed-point method. To find for the approximate error of this
method can be solve using this formula,
Newton Raphson Method
The widely used for finding the root for approximations to the zeroes of a real
valued function. It converges quickly for the iterations which are near on the desired
root. It also detectsand overcomes the convergences failure.
This method starts with an initial guess which is close to the true root, the
given function is approximated by its tangent line then computes the x-intercept of
this tangent line. This x-intercept will be the approximation to the function's root than
the original guess, and the method can be repeated. The formula for this method is
given by
The termination of the Newton- Raphson method is the same as for computing
the other methods. The convergence depends on the accuracy of the initial guess root
and the nature of the problem.
Secant Method
It is an open method which assumes a function that can be approximately
linear in the region of interest. The formula for the needs two initial estimates of x but
𝜀 𝑎 = (
𝑥 𝑖+1−𝑥 𝑖
𝑥 𝑖+1
) 100% (2.3)
𝑥 𝑖+1 = 𝑥 𝑖 +
𝑓(𝑥 𝑖)
𝑓′(𝑥 𝑖)
(2.4)

9
the f(x) is not required to change the signs between the two estimates and is given by
this equation,
The two values can sometimes lie on the same root and sometimes this can
cause the divergence. The convergence of this method is that the root is within the
bracketing which is the reason that it was compared with the false position method.
Modified Secant Position Method
This method uses an alternative approach which involves the fractional
perturbation of the independent variable to estimate the f’(x) instead of using the two
arbitrary values. The formula for the iteration is given by
Bairstow’s Method
It is a method that finds complex roots of a polynomial of a quadratic formula
and can be used for solving the root all kinds of a polynomial. It uses the Newton’s
method to adjust the coefficients u and v in the quadratic x2 + ux + v until its roots are
also roots of the polynomial being solved. The root can be found be found by dividing
the polynomial by the quadratic to eliminate the roots and then it can be repeated
until the polynomial becomes quadratic or linear and all roots will be determined. The
values of u and v can be found by picking the starting and repeating the Newton’s
method in two dimensions until it converges, for the quadratic equations of
𝑥 𝑖+1 = 𝑥1 −
𝑓( 𝑥𝑖) 𝑓(𝑥𝑖−1−𝑥𝑖)
𝑓( 𝑥𝑖−1−𝑥 𝑖)−𝑓(𝑥𝑖)
(2.5)
𝑥 𝑖+1 = 𝑥 𝑖 −
𝛿 𝑥 𝑖 𝑓( 𝑥𝑖)
𝑓( 𝑥 𝑖+𝛿𝑥𝑖)−𝑓( 𝑥 𝑖)
(2.6)

10
multiplicity higher than one it converges to that factor is a linear and quadratic factors
that have a small value which has real roots will tend to diverge to infinity. To find for
the zero of polynomial can be implemented with a programming language.
Müller's method
A root finding method that solves for the root of the form f(x) = 0 of the single variable x
and a scalar function whenever there’s no information about the derivatives that
exists. It’s the generalizes the secant method but it uses three points of quadratic
interpolation noted by as xk, xk-1 and xk-2.The The parabola going through the three
points (xk, f(xk)), (xk-1, f(xk-1)) and (xk-2, f(xk-2)) when
It can be written in the Newton form, where f[xk, xk-1] and f[xk, xk-1, xk-2] denote
divided differences;
where;
Brent’s Method

11
It is a method that combines that bisection method, the secant method. The
idea is to use thesecant method because they converge faster, but to fall back to the
more robust bisection method if necessary.
Given a specific numerical tolerane δ, | δ | < | bk − bk − 1 |must hold and the
results is used in the iteration and if previous step is performinterpolation then the
inequality gives | δ | < | bk − 1 − bk − 2 |. Also, if the previous step used the bisection
method, the inequality must hold, otherwise the bisection
method is performed and the result used for the next iteration. If the previous step
performed interpolation, then the inequality is used
instead. Most of the N2 iterations, where N denotes the number of iterations for the
bisection method, if the function f is well-behaved, and this method will usually
proceed by either inverse quadratic or linear interpolation, in which case it will
converge linearly.
Chapter III
Source Code
The following are the listing for the source code of the different methods of
obtaining the root of the function.
Listing 1. Class Main
/* Main Class
- contains the main method which executes the Java
application
- calls the needed methods*/
//import Java extension packages
import javax.swing.JOptionPane;
public class Main {

12
break;// done processing case
}
case 1:{
c.FalsePosition();
}
case 2:{
d.FixedPointIteration();
}
case 3:{
e.NewtonsRaphson();
}
case 4:{
f.Secant();
}
case 5:{
g.Brent();
}

13
Listing 1 contains the source code of the Main class, the class which contains
the main method, a method that executes the application.
Listing 2.Class MRZ
/*MRZ class
- declares method of the function
- declares methods to prompt user to input values needed in the
methods
- declares the method in giving the output*/
//Declaring methods
//import Java extension packages
import javax.swing.*;
//import Java core packages
import java.text.DecimalFormat;
public class MRZ {
//Create JTextArea to display output
JTextArea Mrz = new JTextArea (25,75);
//Puts a scrollbar in the JTextArea
JScrollPane mRz = new JScrollPane(Mrz);
DecimalFormat df = new DecimalFormat("0.00000000");
public static MRZ mrz = new MRZ();

14
}//end method input
//Function of the given problem
public double func(double N){
return ((Math.pow(j, -1)))-(N/2)-
(Math.sqrt(Math.pow(N,2)+
4*Math.pow(ni,2)))/2;//returns the function
}
//g(x) of the function of the given problem
public double gfunc(double N){
return (Math.pow(j,-1))-(N/2)-
(Math.sqrt(Math.pow(N,2)+4*Math.pow(ni,2)))/2+N;
}
//Derivative of the function of the given problem
public double dfunc(double N){
return -(0.5)-((N*(1/(Math.sqrt(Math.pow(N,2)+
4*Math.pow(ni,2)))))/2);//return the derivative of the function
}
//Calculates the Approximation Error
public double ea(){
return Math.abs((Nr-Nrold)/Nr)*100;//returns the Approximate

15
NU=JOptionPane.showInputDialog("Input upper limit: ");
Nl=Double.parseDouble(NL);
Nu=Double.parseDouble(NU);
//check if the given interval contains one root
if (mrz.func(Nl)*mrz.func(Nu)>0)
{
b=0;
JOptionPane.showMessageDialog(null,"The root is not
" +"located in the given interval or there are more
" +"than one
root","Notification",JOptionPane.WARNING_MESSAGE);
}
else b=1;
}//end while structure
}
// determine the method to use based on user's choice
switch(s){
case 2://Fixed-Point Iteration Method
{
NO=JOptionPane.showInputDialog("Enter initial guess:

16
estimate of x: ");
N0=Double.parseDouble(NO);
if (N0==0)
{
b=0;
JOptionPane.showMessageDialog(null,"INVALID! Enter
another" +" value for x(non-zero).","Notice",
JOptionPane.WARNING_MESSAGE);
}else b=1;
}//end while structure
SIGMA=JOptionPane.showInputDialog("Input pertubation
fraction: ");
sigma=Double.parseDouble(SIGMA);
}
case 5://Brent's Method
{
EPS=JOptionPane.showInputDialog(null,"Enter the
specific " +"numerical tolerance:
");eps=Double.parseDouble(EPS);
}

17
Listing 2 contains the source code of the MRZ class. This class is the Mother
class with six subclasses ModBisection,ModFalsePosition, FixedPointIteration,
NewtonRaphson, ModSecant and Brent. This class contains the conditions of
obtaining correct initial inputs for each of the subclasses.
Listing 3. Listing for Bisection Method
/*ModBisection Class
- class containing the method of the "Modified Bisection
method".*/
public class ModBisection extends MRZ{
public void Bisection(){
//initialize String
wee=" Bisectionn----------nNo of
iter.tXlttXuttXrttEan";
fl = mrz.func(Nl);
for(int iter = 0; iter<imax;iter++){
Nrold=Nr;
Nr=(Nl+Nu)/2;
fr = mrz.func(Nr);
if(Nr != 0) ea = mrz.ea();
else ea=es;
if (fl*fr<0){
Nu = Nr;
}

18
Next is Listing 3 is the source code for the class ModBisection. This class only
consists of the process of the method. The inputs are located in the mother classMRZ.
Listing 4. Listing for False Position
package casestudy;
/*ModFalsePosition Class
- class containing the method of the "False Position
method".*/
public class ModFalsePosition extends MRZ {
public void FalsePosition(){
double il=0,iu=0;
//initialize String
wee="False Positionn----------nNo of
iter.tXlttXuttXrttEan";
fl = mrz.func(Nl);
fu = mrz.func(Nu);
for(int iter=0; iter<imax;iter++){
Nrold=Nr;
Nr=Nu-fu*(Nl-Nu)/(fl-fu);
fr=mrz.func(Nr);
if (Nr!=0)ea=mrz.ea();
else ea=es;
if ((fl*fr)<0){

19
Listing 4 contains the source code of the class ModFalsePosition. This
class contains only the method’s process, input proper appears in the
Mother class MRZ
Listing 5. Listing for Fixed Point Iteration
/*FixedPointIteration Class
- class containing the method of the "Fixed-Point Iteration
method".*/
public class FixedPointIteration extends MRZ {
public void FixedPointIteration(){
//initialize string
wee = "Fixed-Point Iterationn----------nNo of
iter.tXottXrttEan";
Nr=N0;
for( int iter = 0; iter<imax;iter++){
Nrold=Nr;
Nr = mrz.gfunc(Nrold);
if(Nr!=0) ea=mrz.ea();
else ea=es;

20
Listing 5 shows the source code of the class FixedPointIteration. Just like the
previous listings, this class contains only the process of the method, the inputs are
located in the Mother class MRZ.
Listing 6. Listing for Newton-Raphson
/*NewtonsRaphson Class
- class containing the method of the "Newton's Raphson
method".*/
public class NewtonsRaphson extends MRZ{
public void NewtonsRaphson(){
//initialize String
wee = "Newton's Raphson Methodn----------nNo of
iter.tXottXrttEan";
Nr=N0;
Nrold=Nr;
Nr = Nrold-(mrz.func(Nrold))/(mrz.dfunc(Nrold));
if(Nr!=0) ea=mrz.ea();
else ea=es;
if (iter==0)
wee += (iter+1)+"t"+df.format(Nrold)+"t"+
df.format(Nr)+"t-----n";
else
df.format(Nr)+"t"+df.format(ea)+"n";
if(ea<es) break;

21
Listing 6 contains the source code of the Newton-Raphson method. This
contains the process of the said method. The inputs are located in the Mother class
MRZ.
Listing 7. Listing for Secant Method
/*ModSecant Class
- class containing the method of the "Modified Secant
method".*/
public class ModSecant extends MRZ {
public void Secant(){
//initialize String
wee ="Secant Methodn----------nNo of
iter.tXottXrttEatn";
double fa,fb;
Nr=N0;
Nrold=Nr;
fa = mrz.func(Nrold);
fb = mrz.func(Nrold+(sigma*Nrold));
Nr = Nrold -(sigma*Nrold*fa)/(fb-fa);
if(Nr!=0)ea=mrz.ea();
else ea=es;
if(iter==0)
df.format(Nr)+"t-----n";
else

22
Listing 7 contains the source code of the class ModSecant. Just like the
previous subclasses, this only contains the process proper of the method. The inputs
are located in the Mother class MRZ. The next is Listing 8, which contains the source
code of the class Brent, like previous subclasses, this contains the process of the
method. The input proper is located in the Mother class MRZ.
Listing 8. Brent’s Method
/*Brent Class
- class containing the method of the "Brent's method".*/
public class Brent extends MRZ {
public void Brent (){
//Initialize String
wee = "Brent's Methodn----------nNo of
iter.tXrttEan";
double fc,c, c0, c1, c2,temp, mtflag, d;
int mflag,iter = 1;
c = Nl;
d = c;
fl = mrz.func(Nl);//fa=fl
fu = mrz.func(Nu);//fb=fu
fc = mrz.func(c);
if ( Math.abs(fl) < Math.abs(fu))
{
temp = Nl;
Nl = Nu;
Nu = temp;
temp = fl;
fl = fu;
fu = temp;
}
mflag = 1;
while ( (Math.abs(fu) > eps) && ( Math.abs(Nu-Nl) > eps))

23
Chapter IV
else
mflag = 0;
fr = mrz.func(Nr);
d = c;
c = Nu;
fc = fu;
if(Nr !=0)ea=mrz.ea();
else ea=es;
if ( (fl*fr)< 0)
Nu = Nr;
else
Nl = Nr;
if ( Math.abs(fl) < Math.abs(fu))
{
temp = Nl;
Nl = Nu;
Nu = temp;
temp = fl;
fl = fu;
fu = temp;
}
if (iter==1)
wee += iter+"t"+df.format(Nr)+"t-----n";
else
wee += iter+"t"+df.format(Nr)+"t"+ea+"n";
if (ea<es) break;
iter++;

24
Result
A. Graphical Result
Chapter IV
Results and Discussion
A. Graphical Representation
0.001
0.01
0.1
1
10
100
pproximateError
Bisection
False
Position
Fixed-Point
Iteration
Newton's
Raphson

25
Figure 1 shows the graphical representation between the approximate errors(𝜖 𝑎)
and the number of iterations. The results were obtained through the use of the
different methods stated.
B. Screenshot of outputs
The following figures are the actual results or screenshots obtained using the
source codes accessible on Chapter 3.

26Figure 4. Screenshot of the Result for Fixed Point Iteration
Figure 3. Screenshot of the Result for False Position Method

27
Figure 5. Screenshot of the Result for Newton-Raphson Method
Figure 6. Screenshot of the Result for Secant Method

28
C. Table of Results
The following are the tabular presentation of the results obtained after
employing the different methods for solving the function eq. 5.
Figure 7. Screenshot of the result for Brent’s Method
Table 1. Results for Bisection Method
Iterations Nr εa
1 15000000000 -----
2 12500000000 20
3 11250000000 11.1111111
4 11875000000 5.26315789
5 11562500000 2.7027027
6 11718750000 1.33333333
7 11796875000 0.66225166
8 11757812500 0.33222591
9 11738281250 0.16638935

29
Table 1 shows the obtained results for solving the roots of eqn. 5 using the
Bisection Method. As shown, the root was obtained after 11 iterations and is equal to
Nr = 11752929688, where the condition εa< εs was satisfied after 11 iterations such
that εa = 0.0415454, which is less than the inputted stopping εs =0.05. The limits used
in solving the problem are 1x1010 and 2x1010, the lower and upper limits respectively.
Table 2 shows the obtained results for solving the roots of the function eqn. 5
using the False Position Method. As seen above, the root was obtained after
4iterations, which was evaluated from the lower and upper limits, 1x1010 and 2x1010
respectively, where the value of the approximation error is εa = 0.04073353, which
satisfies the condition εa< εs, where εs = 0.05.
Table 2. Results for False Position Method
Iterations Nr εa
1 11655417267 -----
2 11751253575 0.81554115
3 11761402241 0.08628788
4 11756613357 0.04073353
Table 3. Results for Fixed-Point Iteration Method
Iterations Nr εa
1 11456538023 -----
2 11709015931 2.15626923
3 11749157662 0.34165624
4 11755447971 0.05350973
5 11756431421 0.00836521

30
Table 3 shows the obtained results for solving the roots of the function in eqn. 5
using the Fixed-Point Iteration Method. From the table, a root of Nr = 11756431421 is
obtained after 5 iterations, where the condition εa< εs is satisfied, where εa =
0.00836521 and εs = 0.05. The initial guess used is 1x1010.
Table 4 shows the obtained results for solving the function in eqn.5 using the
Newton-Raphson Method. From the table, a root of Nr = 11756613591 is obtained
after 3 iterations with a relative approximate error of εa = 0.00008794, which satisfies
the condition εa< εs, where εs = 0.05. The initial guess used is 1x1010.
Table 5 shows the results after computing for the root of the function in eqn. 5
using Modified Secant Method where the root was found out to be equal to
Table 4. Results for Newton-Raphson Method
Iterations Nr εa
1 11790305201 -----
2 11756623930 0.28648762
3 11756613591 0.00008794
Table 5. Results forSecant Method
Iterations Nr εa
1 11780101085 -----
2 11756741026 0.19869502
3 11756614257 0.00107828

31
Nr=11756614257. This root was obtained in the 3rd iteration where the relative
approximate error is equal εa=0.00107828 which is less than the required stopping
condition εs=0.5. The perturbation factor used is 0.05, and the initial estimate used is
1x1010.
The table above shows the results obtained after computing for the root of the
function in eqn. 5 by employing Brent’s Method. As shown above, the root, Nr =
11748046875, was obtained in the 10th iteration where the computed approximate
error Es=0.08312552 satisfiesthe terminating condition εa<εs where εs = 0.05.
In evaluating the root of the function using theformula for Brent’s Method, the
lower and upper limit used were 1x1010 and 2x1010 respectively, and the numerical
tolerance was chosento be equal to 0.000001.
Table 6. Results forBrent’s Method
Iterations Nr εa
1 15000000000 -----
2 12500000000 20
3 11250000000 11.11111111
4 11875000000 5.263157895
5 11562500000 2.702702703
6 11718750000 1.333333333
7 11796875000 0.662251656
8 11757812500 0.332225914
9 11738281250 0.166389351
10 11748046875 0.08312552

32
Chapter V
Conclusion
The Newton-Raphson Method gives the least approximate true error over other
methods in finding the root of equation (5). Equation (5) is much more approximately
equal to zero when the root obtained using the Fixed Point Iteration methodis
substituted. In addition, these methods give a lesser relative approximation error,
though εa and εt for this technique has a considerable difference compared to the other
methods.
With our given function, the Newton Raphson is the most efficient technique in
finding the root of the function in equation (5). This is true since only a single value is

33
used to predict succeeding values for the root estimate since it uses the least number
of iterations to obtain the root. A better accuracy is also attained with this method
since, it ensures a better convergence other than the methods, and since equation (5)
is a linear function the Muller and Bairstow’s Method cannot be applied because
primarily these methods can only be applied for polynomial functions.
Homework Help
Math homework help
Research Paper help
Algebra Help
Calculus Help
Accounting help
Paper Help

34
Writing Help
Online Tutor
Online Tutoring

83662164 case-study-1

More Related Content

What's hot

Viewers also liked

Similar to 83662164 case-study-1

More from homeworkping3

Recently uploaded

83662164 case-study-1