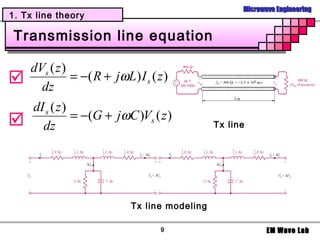
1. The document discusses transmission line theory and parameters. Key topics covered include: - Telegrapher's equation and circuit model for transmission lines - Wave propagation and characteristic impedance calculations - Reflection coefficient and standing wave ratio definitions - Comparisons of transmission line, circuit, and field theories 2. Specific transmission line types are analyzed, including planar lines, coaxial cables. Equations are given for calculating the capacitance, conductance, inductance, resistance, and characteristic impedance of these common line configurations. 3. Simulation and modeling techniques for transmission lines are briefly mentioned, such as the transmission line matrix method for modeling microstrip lines in antennas and circuits.

1. Transmission
Line
Microwave Engineering
CHO, Yong Heui

2. Microwave Engineering
1. Tx line theory
Telegrapher’s equation
  Communication service: telegraph
Telegraph
Ocean
2 EM Wave Lab

3. Microwave Engineering
1. Tx line theory
World wide transmission lines
EM Wave Lab

4. Microwave Engineering
1. Tx line theory
Introduction
  The differential equations which the voltage or
current must satisfy on a uniform transmission
line.
 Circuit model: tie field theory and circuit theory
together.
 Our circuit model contain the inductance L,
capacitance C, shunt conductance G, and series
resistance R associated with an incremental
length of line.
 Coaxial transmission line containing a dielectric.
4 EM Wave Lab

5. Microwave Engineering
1. Tx line theory
Wave propagation
 V ( z , t ) = Vo cos(ωt − βz + φ )
= Re{Vo e j (ωt − βz +φ ) }
jφ − jβz j ωt
= Re{Vo e e e }
5 EM Wave Lab

6. Microwave Engineering
1. Tx line theory
Distributed element
  Lumped element: R, L, C
  Distributed element: tx line
6 EM Wave Lab

7. Microwave Engineering
1. Tx line theory
Circuit model
ˆ
 Propagation in the a z direction
Length ∆z : R∆z[ Ω], L∆z[ H ], G∆z[1 / Ω], C∆z[ F ]
lim: infinitesimal approach
∆z →0
7 EM Wave Lab

8. Microwave Engineering
1. Tx line theory
Transmission line equation
 Phasor : Vs ( z ) = Vo e jφ e − jβz
1 1 
Vs ( z ) =  R∆z + jω L∆z  I s ( z )
2 2 
1 1 
+  R∆z + jω L∆z ( I s ( z ) + ∆I s ( z )) + Vs ( z ) + ∆Vs ( z )
2 2 
∆Vs ( z ) 1 1 
= −( R + jωL) I s ( z ) −  R + j ωL ∆I s (z) : As ∆z → 0, ∆I s → 0
 ∆z 2 2 
∆I s ( z ) ∆Vs ( z )
− = (Vs ( z ) + )(G + jωC ) : As ∆z → 0, ∆Vs → 0
∆z 2
8 EM Wave Lab

9. Microwave Engineering
1. Tx line theory
Transmission line equation
dVs ( z )
 = − ( R + jω L ) I s ( z )
dz
dI s ( z )
 = −(G + jωC )Vs ( z )
dz Tx line
Tx line modeling
9 EM Wave Lab

10. Microwave Engineering
1. Tx line theory
Wave solution
  Traveling wave solution
+ −γz
- Voltage: Vs ( z ) = V0 e + V0− eγz
- Current: I s ( z ) = I 0+ e −γz − I 0− eγz
d 2Vs ( z )
2
= ( R + jωL)(G + jωC )Vs ( z )
dz
γ = α + jβ = ( R + jωL)(G + jωC )
10 EM Wave Lab

11. Microwave Engineering
1. Tx line theory
Characteristic impedance
  Important parameter in tx line: Z0
R + j ωL
- Z0 =
G + j ωC
V0+ V0−
- Z0 = + = −
I0 I0
11 EM Wave Lab

12. Microwave Engineering
1. Tx line theory
Lossless line
 γ = jβ = jω LC
L
 Z0 =
C
+ − jβz − − jβz
 Vs ( z ) = V e
0 +V e0
+ −
V − jβz V jβz
I s ( z) = 0
e − e0
Z0 Z0
12 EM Wave Lab

13. Microwave Engineering
1. Tx line theory
Low-loss line
 γ = α + jβ = ( R + jωL)(G + jωC )
 j R G 
≈ jω LC 1 −  + 
 2  ωL ωC  
1 R 
 α =  + GZ 0 
2  Z0



L
 Z0 ≈
C
13 EM Wave Lab

14. Microwave Engineering
1. Tx line theory
Distortionless line
R
γ = α + jβ = + jω LC
 Z0
L
 Z0 =
C
14 EM Wave Lab

15. Microwave Engineering
1. Tx line theory
Reflection coefficient
  Voltage wave continuity conditions
 Current wave continuity conditions
Vo− Z L − Z 0
 Γ11 =| Γ | e jφ = + =
V0 Z L + Z0
15 EM Wave Lab

16. Microwave Engineering
1. Tx line theory
Wave power
+ 2

1
P = Re VI =
2
*
V
( )
2Z 0
0
1− Γ
2
( )
16 EM Wave Lab

17. Microwave Engineering
1. Tx line theory
SWR (Standing Wave Ratio)
  SWR: field theory
 VSWR (Voltage SWR): tx line theory
V
s= max
V min
1+ | Γ |
=
1− | Γ |
Experiment
17 EM Wave Lab

18. Microwave Engineering
1. Tx line theory
Comparison with circuit theory
18 EM Wave Lab

19. Microwave Engineering
1. Tx line theory
Comparison with circuit theory
19 EM Wave Lab

20. Microwave Engineering
1. Tx line theory
Comparison with circuit theory
20 EM Wave Lab

21. Microwave Engineering
1. Tx line theory
Comparison with field theory
For comparison, ∇ × E s = − jωµH s
Set E s = E xs a x and H s = H ys a y
where E xs and H ys are functions of z only.
dE xs dVs
 = − jωµH ys ⇔ = − ( R + j ωL ) I s
dz dz
∇ × H s = (σ + jωε )E s
dH ys dI s
 = −(σ + jωε ) E xs ⇔ = −(G + jωC )Vs
dz dz
21 EM Wave Lab

22. Microwave Engineering
1. Tx line theory
Comparison with field theory
 A direct analogy : I s and H ys , G and σ , C and ε , Vs and E xs
The boundary conditions on Vs and E xs
are the same to those for I s and H ys .
 E xs = E x 0 e − jkz , jk = jωµ (σ + jωε )
⇔ Vs = V0 e −γz , γ = α + jβ = ( R + jωL)(G + jωC )
 For a lossless line ( R = G = 0)
2π ω
1 β= vp =
γ = jβ = jω LC , v p = λ β
LC
22 EM Wave Lab

23. Microwave Engineering
1. Tx line theory
Reflection coefficient
E x 0 − jkz V0 − jβz
 H ys = e ⇔ Is = e
η Z0
( Z 0 : characteristic impedance)
jωµ R + jωL
η= ⇔ Z0 =
σ + jωε G + jωC
E x−0 η 2 − η1 Vo− Z 02 − Z 01
 Γ11 = + = ⇔ Γ11 =| Γ | e jφ = + =
E x 0 η 2 + η1 V0 Z 02 + Z 01
23 EM Wave Lab

24. Microwave Engineering
1. Tx line theory
Input impedance
 The ratio of Vs to I s at z = −l
when Z = Z 2 for z > 0 and Z = Z1 for z < 0 :
η 2 cos β1l + jη1 sin β1l
 ηin = η1 η cos β l + jη sin β l
1 1 2 1
Z 2 cos β1l + jZ1 sin β1l
⇔ Z in = Z1
Z1 cos β1l + jZ 2 sin β1l
24 EM Wave Lab

25. Microwave Engineering
1. Tx line theory
TLM (Transmission Line Matrix)
 Equivalence: field theory and tx line theory
 Simulation tool: Micro-stripes based on TLM method
Bluetooth antennas
Current density
25 EM Wave Lab

26. Microwave Engineering
1. Tx line theory
Antenna impedance
  Antenna impedance (not infinity) matching
 No reflection, power efficiency
Handy phone antenna
26 EM Wave Lab

27. Microwave Engineering
2. Tx line parameters
Planar line
 Assume b >> d
εb σ σb
C = ,G = C =
d ε d
µd 2
Lext = ,R =
b σ c bδ
Lext µ d Cross section
 Z0 = =
C ε b
27 EM Wave Lab

28. Microwave Engineering
2. Tx line parameters
Coaxial line
ρL
 ∫S D • dS = Q 2πρLD = ρ L L D = 2πρ a ρ
ρL
E= aρ
2πε ' ρ
a ρL ρ ρ b
Vo = − ∫
a
dρ = − L ln ρ b = L ln
b 2πε ' ρ 2πε ' 2πε ' a
Cross section
2πε
 C= [ F/m]
ln(b / a )
Coaxial line + connector
28 EM Wave Lab

29. Microwave Engineering
2. Tx line parameters
Coaxial line
ε C ε σ 2πσ
 RC = , = , G = C ⇒ G = [1 / Ωm]
σ G σ ε ln(b / a)
µId b µ b
 Φ= ln , Lext = ln [ H / m]
2π a 2π a
1 1 1 1 1
 Rinner = , Router = ⇒R=  + [ Ω / m]
2πaδσ c 2πbδσ c 2πδσ c  a b 
The characteristic impedance of a coax

Lext 1 µ b
Z0 = = ln
C 2π ε a
29 EM Wave Lab