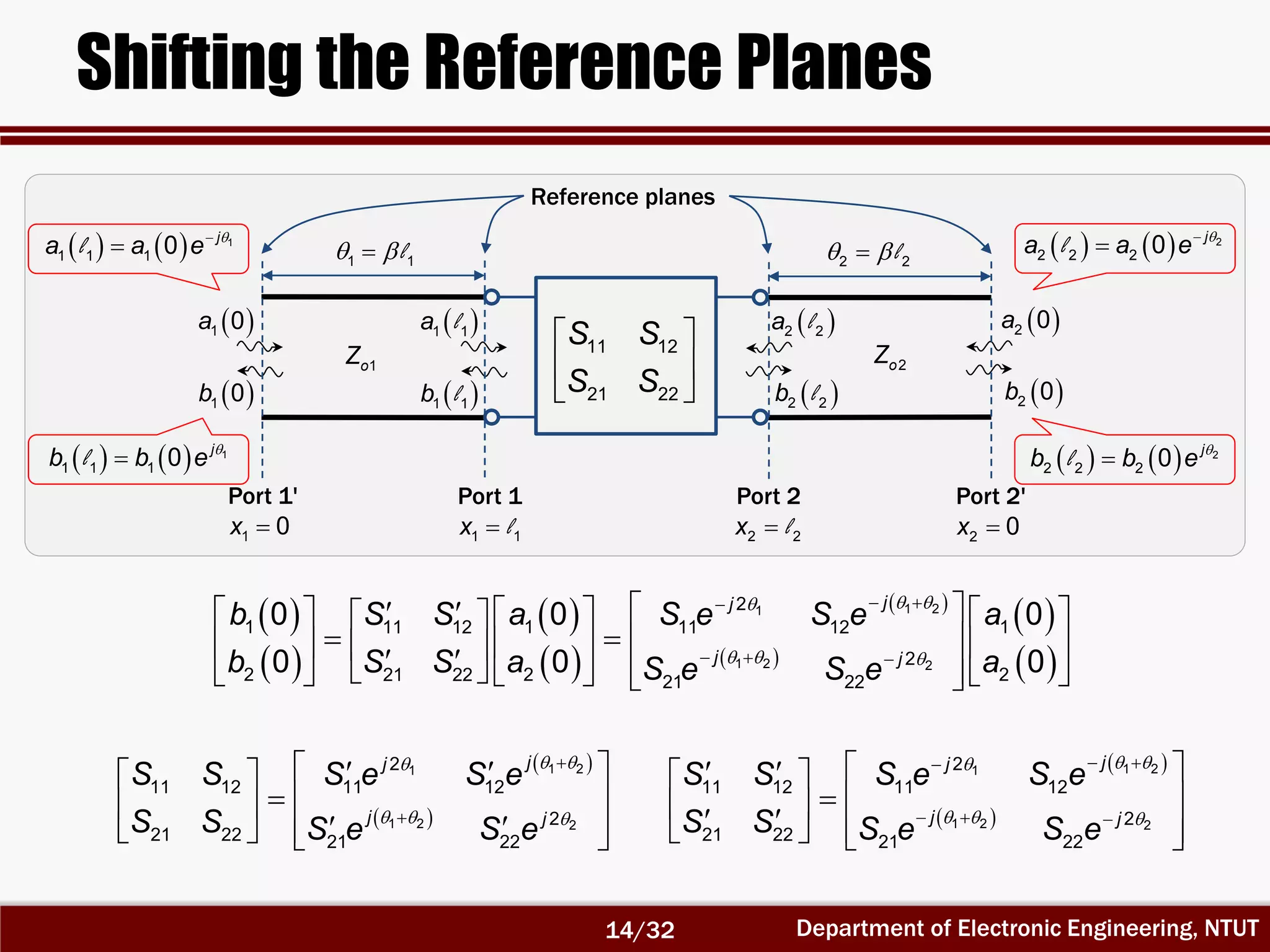
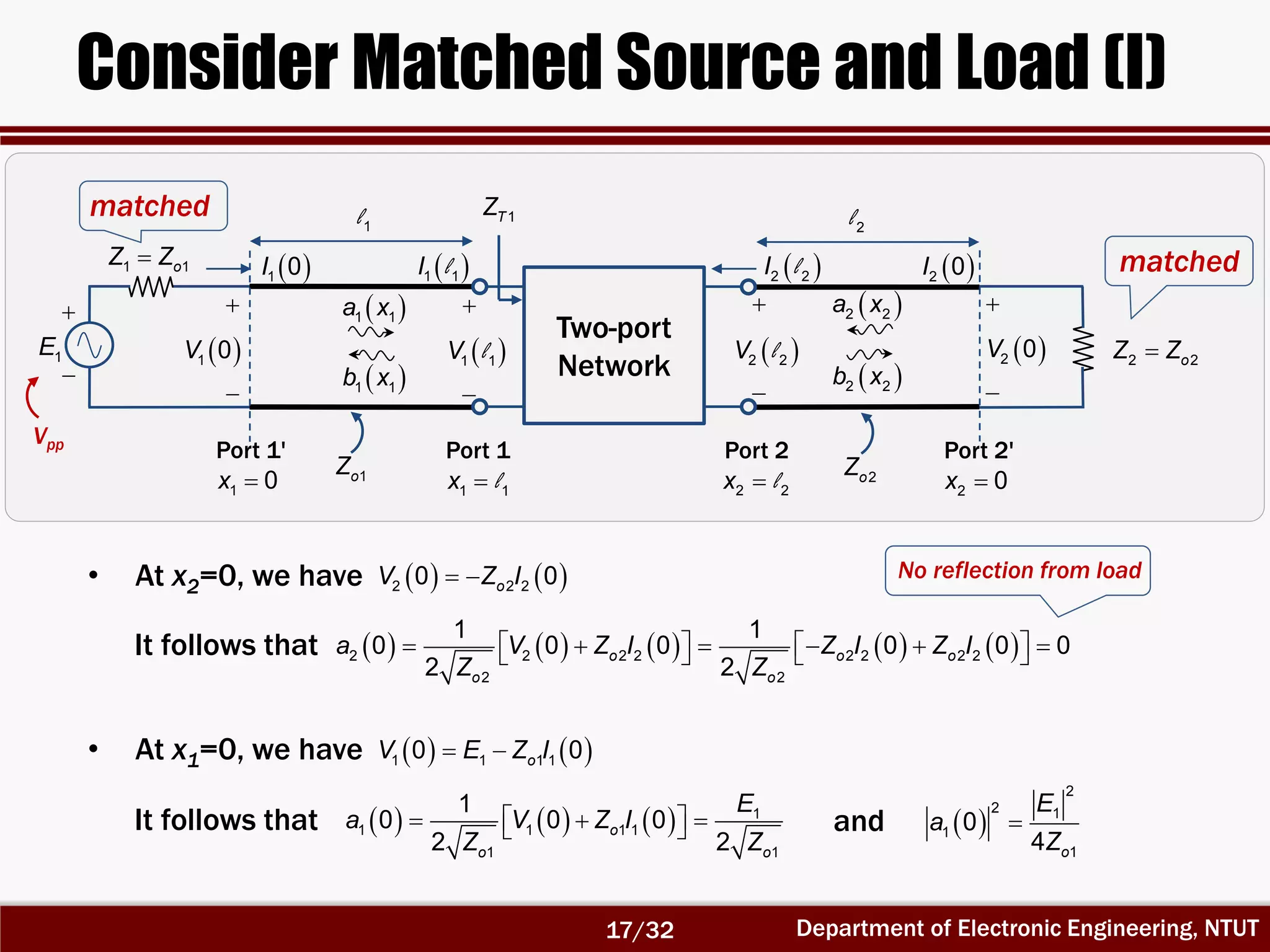
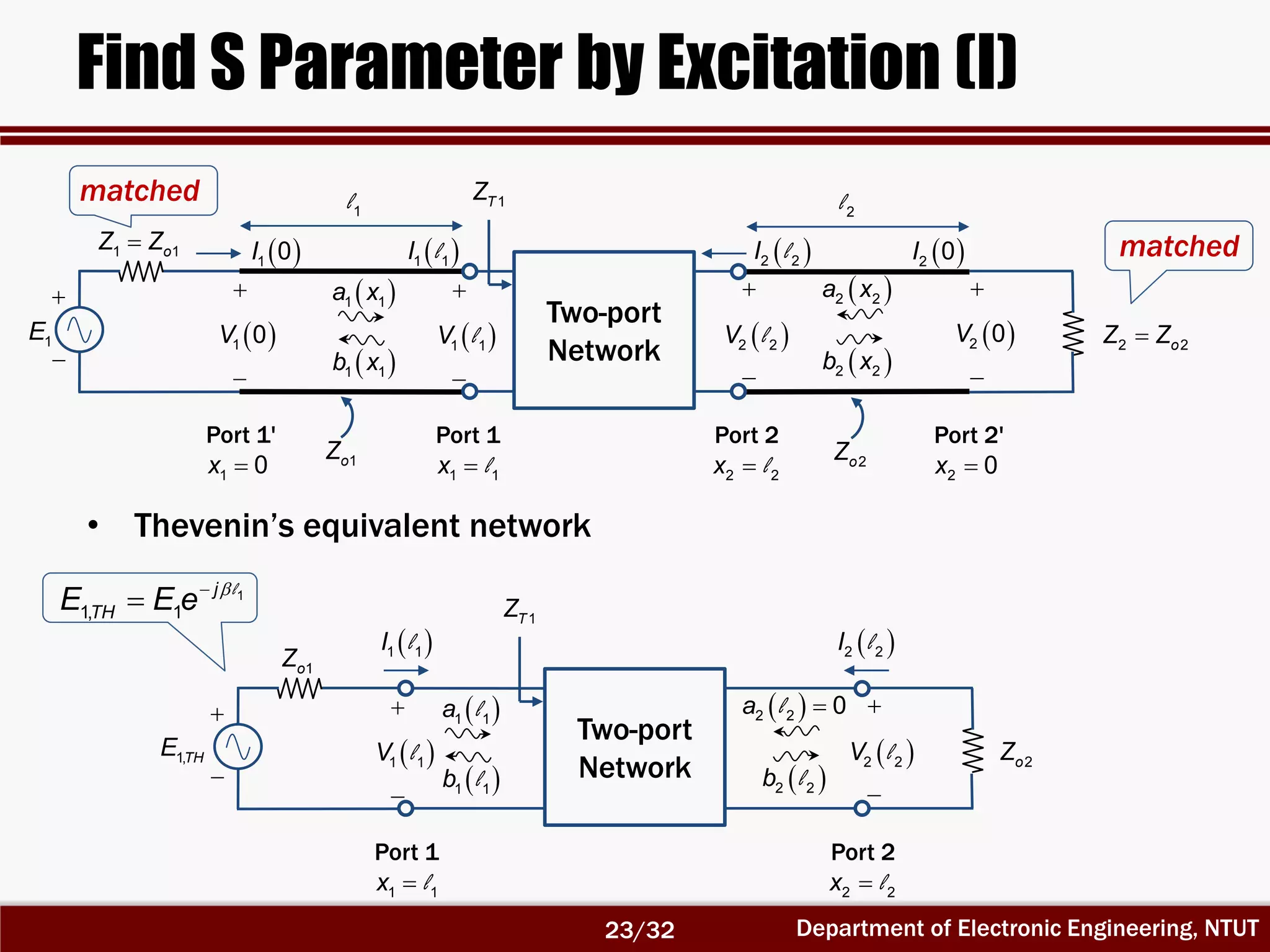
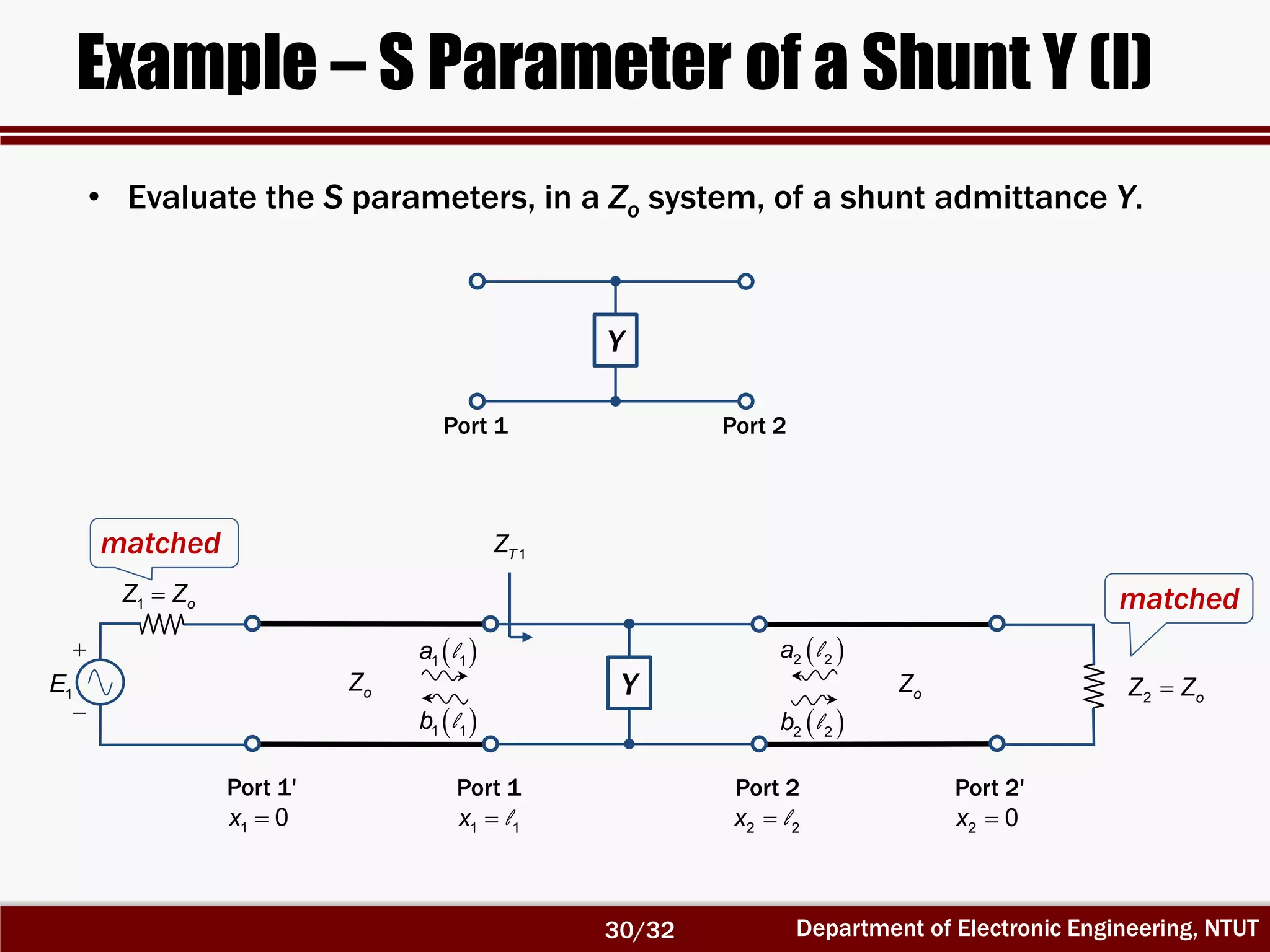
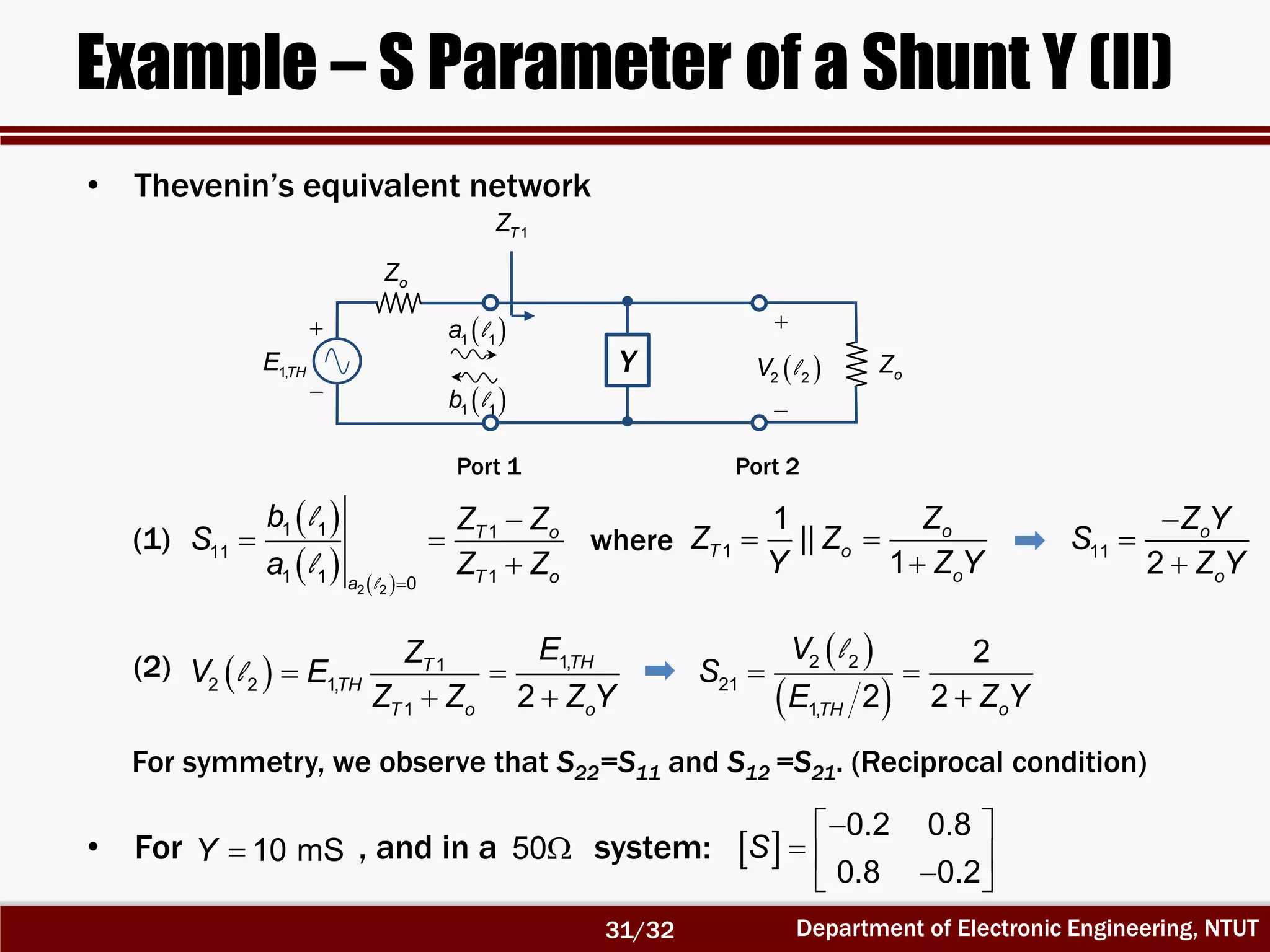
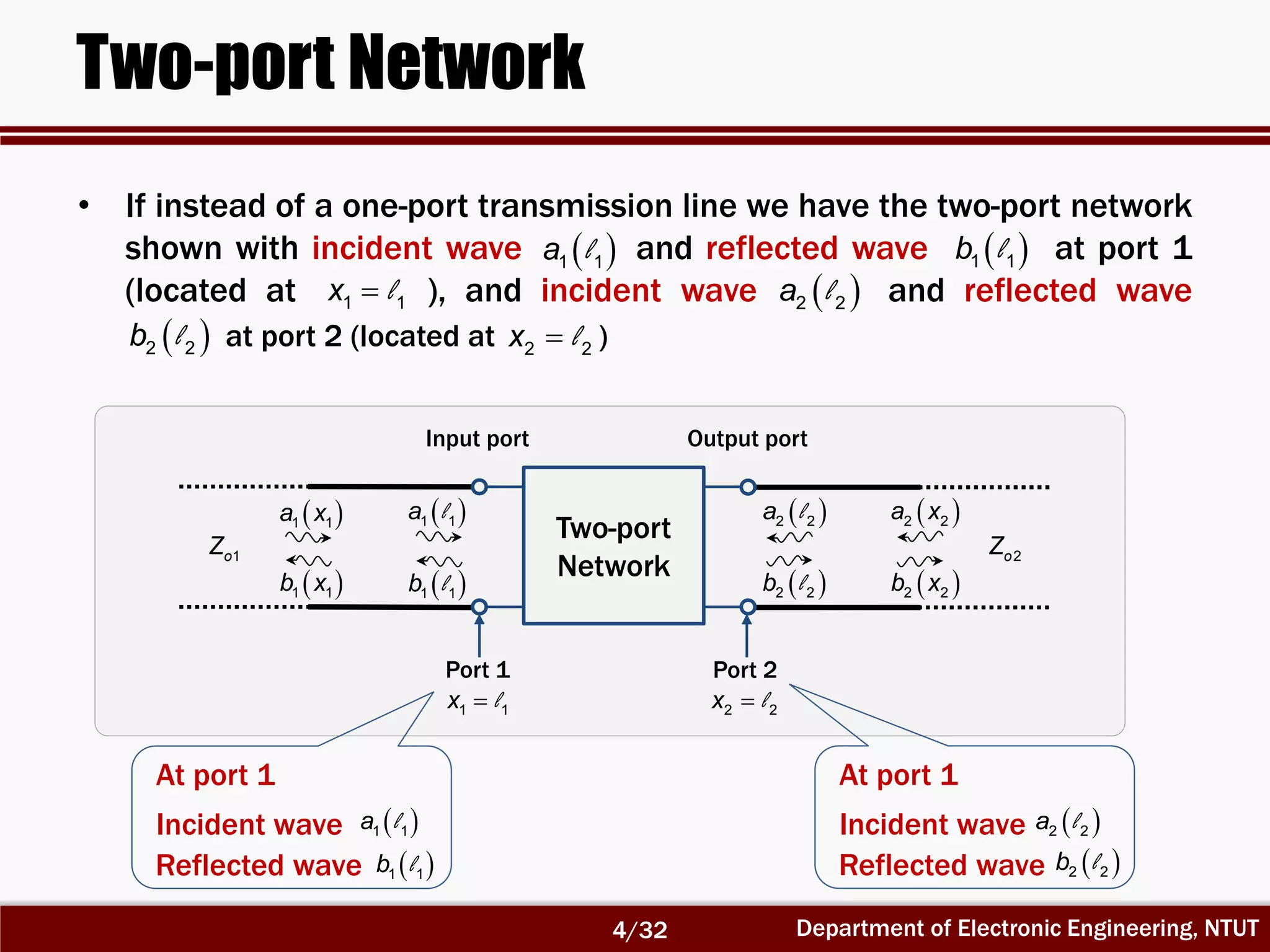
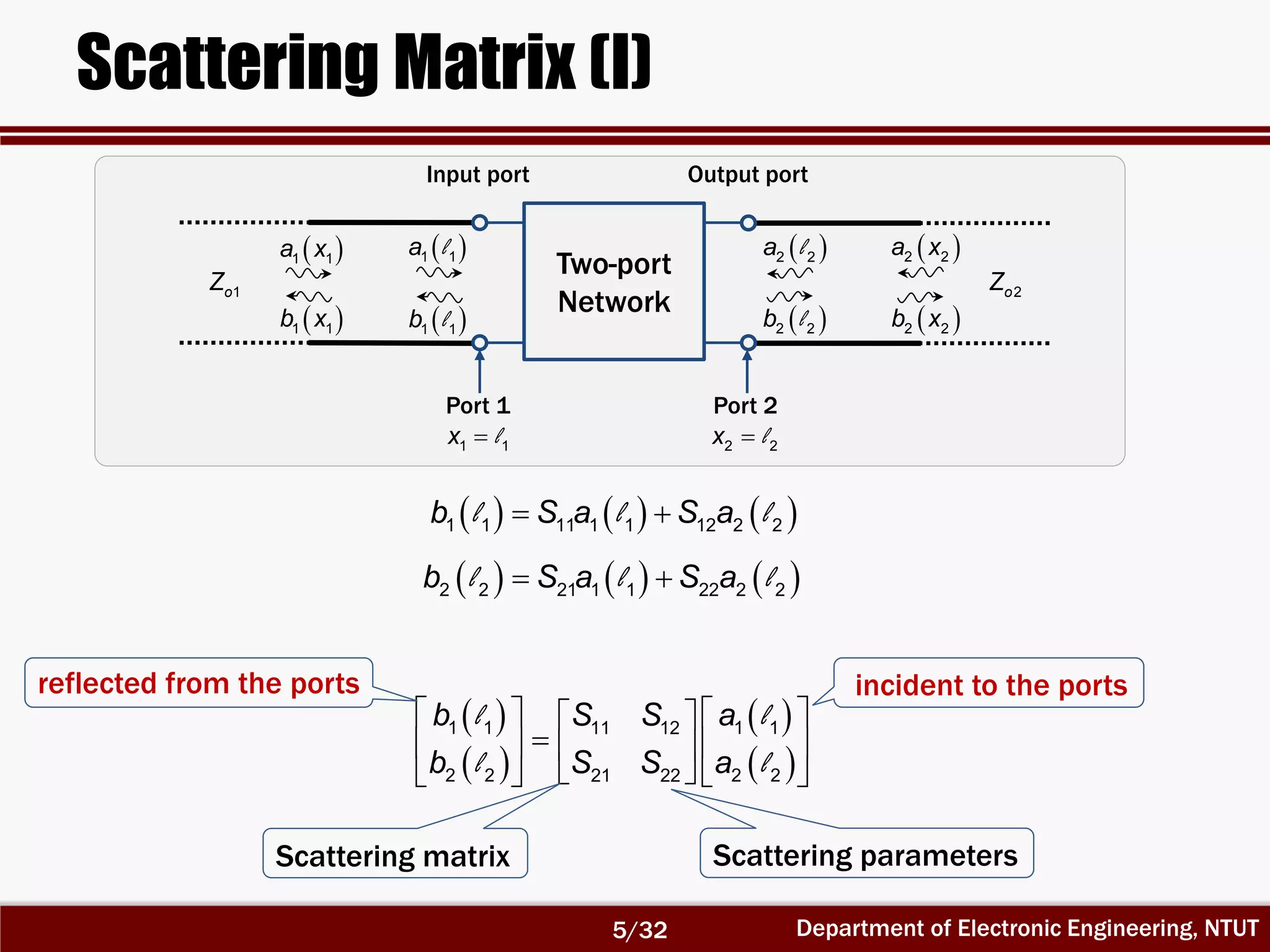
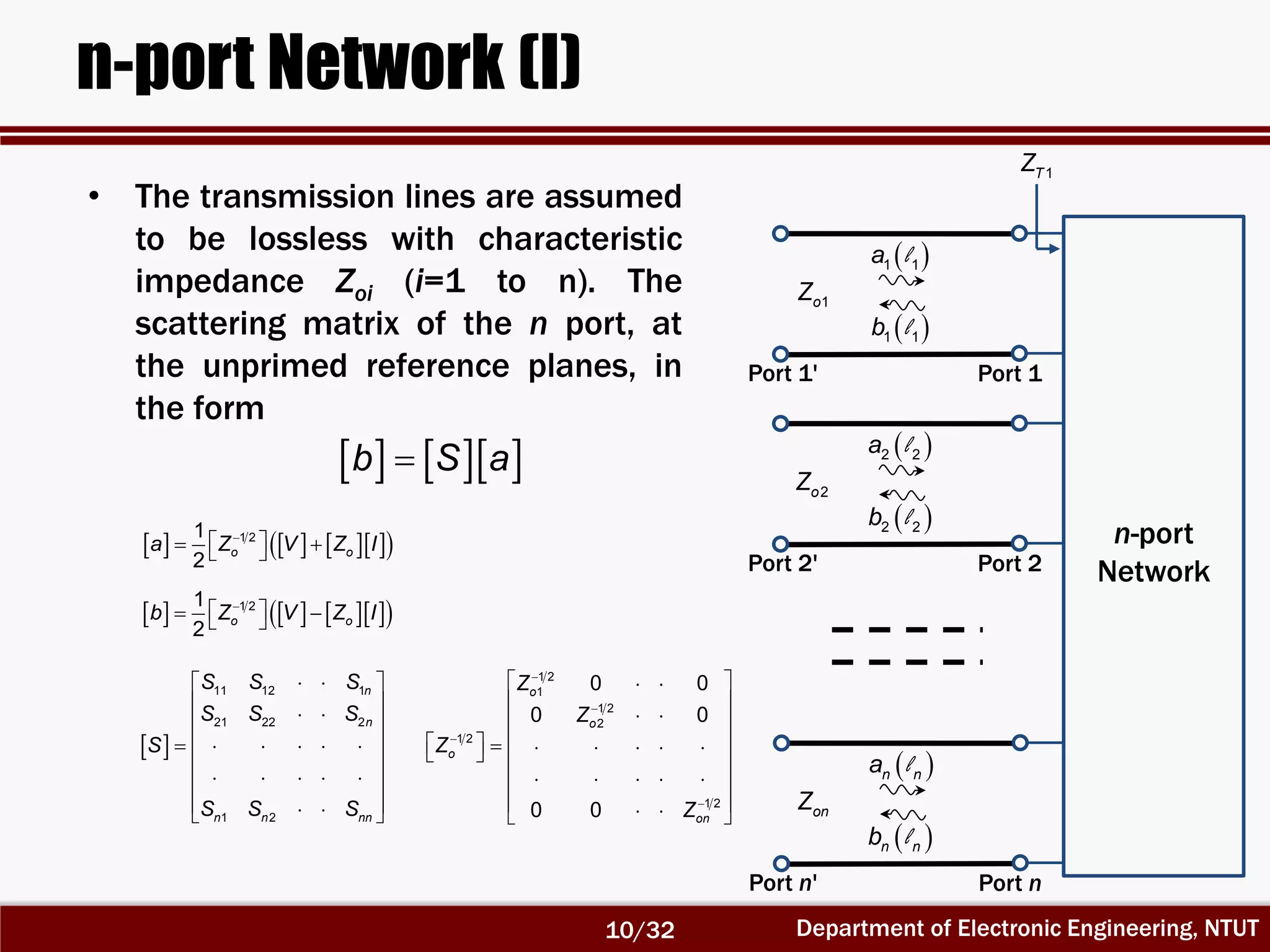
The document discusses the scattering matrix and microwave networks, detailing the concepts of traveling waves, normalized incident and reflected waves, and the use of two-port and n-port networks. It introduces key parameters such as reflection coefficients, transmission coefficients, return loss, and insertion loss alongside measurement procedures. Additionally, it emphasizes the importance of reference planes in practical measurements of the S-parameters.

1. Chapter 3-1
Scattering Matrix and
Microwave Network
Chien-Jung Li
Department of Electronics Engineering
National Taipei University of Technology

2. Department of Electronic Engineering, NTUT
Traveling Waves
   
 j x
V x Ae   
 j x
V x Be
         
   j x j x
V x V x V x Ae Be
     
    
 
   
0 0
V x V x
I x I x I x
Z Z
 
 
 


 
V x
x
V x
• Introducing the notation of the voltage and current traveling
waves:
and
• The reflection coefficient between incident and reflected
wave can be written as:
2/32

3. Department of Electronic Engineering, NTUT
Normalized Traveling Waves
                  0
0
1 1
2 2
b x v x i x V x Z I x
Z
                  0
0
1 1
2 2
a x v x i x V x Z I x
Z
• Normalized notation of voltage and current waves:
 
 
0
V x
v x
Z
    0i x Z I x
 
 

0
V x
a x
Z
 
 

0
V x
b x
Z
      v x a x b x
      i x a x b x
      b x x a x
 Normalized incident wave
 Normalized reflected wave
and
Introduce normalization to
relate voltage with power.
 
 
2
2
0
V x
a x
Z

  
     2
10log 10log 20logaP a x a x 
3/32

4. Department of Electronic Engineering, NTUT
Two-port Network
Two-port
Network
 2 2a l
 2 2b l
 2 2a x
 2 2b x
 1 1a l
 1 1b l
 1 1a x
 1 1b x
1oZ 2oZ
Input port Output port
Port 1
1 1x l
Port 2
2 2x l
• If instead of a one-port transmission line we have the two-port network
shown with incident wave and reflected wave at port 1
(located at ), and incident wave and reflected wave
 1 1a l  1 1b l
1 1x l  2 2a l
 2 2b l 2 2x lat port 2 (located at )
At port 1
Reflected wave
Incident wave  1 1a l
 1 1b l
At port 1
Reflected wave
Incident wave  2 2a l
 2 2b l
4/32

5. Department of Electronic Engineering, NTUT
Scattering Matrix (I)
      1 1 11 1 1 12 2 2b S a S al l l
      2 2 21 1 1 22 2 2b S a S al l l
 
 
 
 
    
    
    
1 1 1 111 12
2 2 2 221 22
b aS S
b aS S
l l
l l
Scattering matrix Scattering parameters
Two-port
Network
 2 2a l
 2 2b l
 2 2a x
 2 2b x
 1 1a l
 1 1b l
 1 1a x
 1 1b x
1oZ 2oZ
Input port Output port
Port 1
1 1x l
Port 2
2 2x l
incident to the portsreflected from the ports
5/32

6. Department of Electronic Engineering, NTUT
Scattering Matrix (II)
contribution to the reflected wave  1 1b l
due to incident wave  2 2a l at port 2
      2 2 21 1 1 22 2 2b S a S al l l
      1 1 11 1 1 12 2 2b S a S al l l
contribution to the reflected wave  1 1b l
due to incident wave  1 1a l at port 1
contribution to the reflected wave  2 2b l
due to incident wave  2 2a l at port 2contribution to the reflected wave  2 2b l
due to incident wave  1 1a l at port 1
Two-port
Network
 2 2a l
 2 2b l
 2 2a x
 2 2b x
 1 1a l
 1 1b l
 1 1a x
 1 1b x
1oZ 2oZ
Input port Output port
Port 1
1 1x l
Port 2
2 2x l
6/32

7. Department of Electronic Engineering, NTUT
Scattering Parameters
 
   

2 2
1 1
11
1 1 0a
b
S
a l
l
l
Input reflection coefficient with output properly terminated
 
   

1 1
2 2
22
2 2 0a
b
S
a l
l
l
Output reflection coefficient with input properly terminated
 
   

2 2
2 2
21
1 1 0a
b
S
a l
l
l
Forward transmission coefficient with output properly terminated
 
   

1 1
1 1
12
2 2 0a
b
S
a l
l
l
Reverse transmission coefficient with output properly terminated
(measured with port 2 properly terminated)
(measured with port 2 properly terminated)
(measured with port 1 properly terminated)
(measured with port 1 properly terminated)
7/32

8. Department of Electronic Engineering, NTUT
Return Loss and Insertion Loss
 
   

2 2
1 1
11
1 1 0a
b
S
a l
l
l
• Return Loss (RL)
 
   

2 2
2 2
21
1 1 0a
b
S
a l
l
l
 
 
2
2 1 1 1
11 2
1 1 1
b
a
b P
S
a P
 
l
l
 21
11 11
1
10log 10log 20log (dB)b
a
P
S S
P
 
  
 
11Return Loss (RL) 10log 20log (dB)in
reft
P
S
P
 
   
 
(折返損耗, 反射損耗)
 
 
2
2 2 2 2
21 2
1 1 1
b
a
b P
S
a P
 
l
l
 22
21 21
1
10log 10log 20log (dB)b
a
P
S S
P
 
  
 
21Insertion Loss (IL) 10log 20log (dB)transmit
receive
P
S
P
 
   
 
(植入損耗, 插入損耗)• Insertion Loss (IL)
8/32

9. Department of Electronic Engineering, NTUT
Procedure of Measuring S11
Two-port
Network
  2 2 0a l
 2 2b l
 1 1a l
 1 1b l
1oZ 2oZ
Port 1
1 1x l
Port 2
2 2x l
2 2oZ Z
1E
1 1oZ Z
 
   

2 2
1 1
11
1 1 0a
b
S
a l
l
l
OUTZ
• With Z2=Zo2 the condition is satisfied. Similar considerations
apply to measurements at the input port. Also the characteristic
impedances of the transmission lines are usually identical (i.e. Zo1=Zo2),
with a 50 Ω being the standard value.
  2 2 0a l
matched
 
   

2 2
1 1
11
1 1 0a
b
S
a l
l
l
      1 1 11 1 1 12 2 2b S a S al l l
0
9/32

10. Department of Electronic Engineering, NTUT
n-port Network (I)
• The transmission lines are assumed
to be lossless with characteristic
impedance Zoi (i=1 to n). The
scattering matrix of the n port, at
the unprimed reference planes, in
the form
    b S a
n-port
Network
1oZ
Port 1Port 1'
1TZ
 1 1a l
 1 1b l
2oZ
Port 2Port 2'
 2 2a l
 2 2b l
onZ
Port nPort n'
 n na l
 n nb l
       
   
1 21
2
o oa Z V Z I
       
   
1 21
2
o ob Z V Z I
 
  
   
      
 
     
   
11 12 1
21 22 2
1 2
n
n
n n nn
S S S
S S S
S
S S S




  
 
  
           
     
   
1 2
1
1 2
2
1 2
1 2
0 0
0 0
0 0
o
o
o
on
Z
Z
Z
Z
10/32

11. Department of Electronic Engineering, NTUT
n-port Network (II)
• The [a], [b], [V], and [I] are column matrices. That is
 
 
 
 
  
 
 
  
1
2
n
a
a
a
a
 
 
 
 
  
 
 
  
1
2
n
b
b
b
b
 
 
 
 
  
 
 
  
1
2
n
V
V
V
V
 
 
 
 
  
 
 
  
1
2
n
I
I
I
I
 
   
l
l  

 

1 1 1 1
11
1 1 1 10 2,3, ,j
T o
T oa j n
b Z Z
S
a Z Z
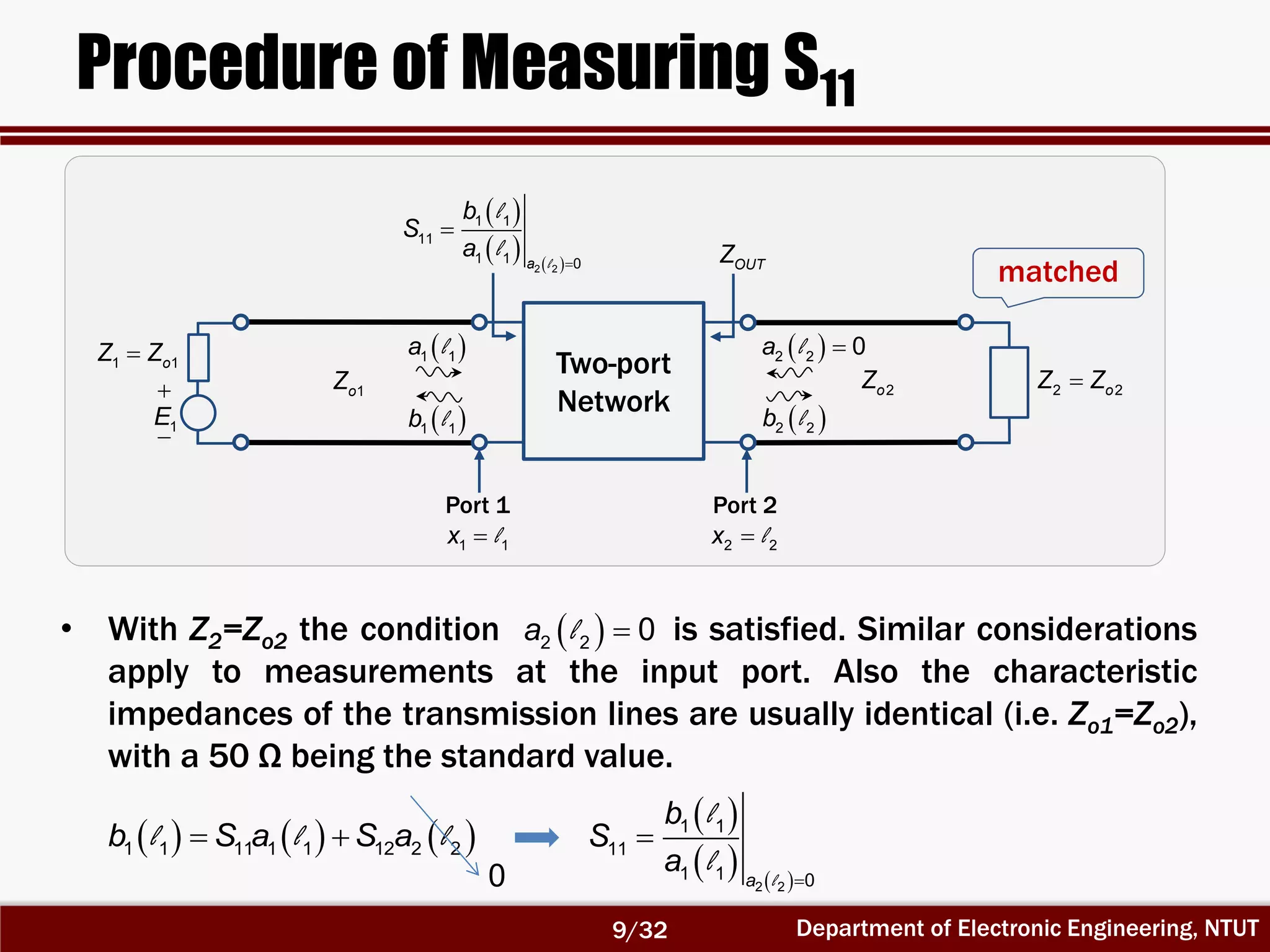
The S parameters of the n-port networks are easily measured.
For example S11 at x1=l1 is given by
where ZT1 is the impedance seen at port 1 with the other ports matched.
11/32

12. Department of Electronic Engineering, NTUT
Reference Planes
• In practice, we often need to attach transmission lines to
the network under test for the measurement. Since the S
parameters are measured using traveling waves, we need
to specify the positions where the measurements are
made.
Device Under Test
(DUT)
1l
2l
Unprimed reference plane
12/32

13. Department of Electronic Engineering, NTUT
Shifting the Reference Planes
 
 
 
 
    
    
    
1 1 1 111 12
2 2 2 221 22
b aS S
b aS S
l l
l l
 
 
 
 
     
         
1 111 12
2 221 22
0 0
0 0
b aS S
b aS S
• At port 1 and port 2
• At port 1' and port 2'
 The angles and are the electrical lengths of the transmission line
between the primed and unprimed reference planes.
Two-port Network
 2 2a l
 2 2b l
 1 1a l
 1 1b l
1oZ 2oZ
Port 1
1 1x l
Port 2
2 2x l
Port 1'
1 0x
 1 0a
 1 0b
Port 2'
2 0x
 2 0a
 2 0b
 2 2l 1 1l
Primed reference plane
1 2
Unprimed reference plane
 
 
 
11 12
21 22
S S
S S
13/32

14. Department of Electronic Engineering, NTUT
Shifting the Reference Planes
    
 1
1 1 1 0 j
b b el
    
 1
1 1 1 0 j
a a el
    
 2
2 2 2 0 j
b b el
    
 2
2 2 2 0 j
a a el
 
 
 
 
 
 
 
 
1 21
1 2 2
2
1 1 111 12 11 12
2
2 2 221 22 21 22
0 0 0
0 0 0
jj
j j
b a aS S S e S e
b a aS S S e S e
 
  
 
  
        
                   
 
 
 
  
 
  
   
         
1 21
1 2 2
2
11 12 11 12
2
21 22 21 22
jj
j j
S S S e S e
S S S e S e
 
 
 
  


   
   
     
1 21
1 2 2
2
11 12 11 12
2
21 22 21 22
jj
j j
S S S e S e
S S S e S e
 2 2a l
 2 2b l
 1 1a l
 1 1b l
1oZ 2oZ
Port 1
1 1x l
Port 2
2 2x l
Port 1'
1 0x
 1 0a
 1 0b
Port 2'
2 0x
 2 0a
 2 0b
 2 2l 1 1l
Reference planes
 
 
 
11 12
21 22
S S
S S
14/32

15. Department of Electronic Engineering, NTUT
Properties of Scattering Parameters
• In order to know the properties of scattering parameters, let’s start
with a two-port network that has two transmission lines attached at
its input and output terminals. (Without considering the source and
load)

1oZ 2oZ
Port 1
1 1x l
Port 2
2 2x l
Port 1'
1 0x
 1 1I x
Port 2'
2 0x
2l1l

 1 1V x
 2 2I x


 2 2V x
 
0iP
 
0iP
 
0iP
 
0iP
• Find the incident power and reflected power .
(i=1 for port 1 and i=2 for port 2)
 
0iP  
0iP
 
 
 
11 12
21 22
S S
S S
15/32

16. Department of Electronic Engineering, NTUT
Incident and Reflected Power
• Average power of incident wave on the primed ith port (x1=0, x2=0)
        
   

  
      
2
2 2
,
01 1 1
0 Re 0 0 0 0
2 2 2
i
i i i i i rms
oi
V
P V I a a
Z
   

21
0 0
2
i iP a
        
   

  
      
2
2 2
,
01 1 1
0 Re 0 0 0 0
2 2 2
i
i i i i i rms
oi
V
P V I b b
Z
• Average reflected power
• Since the transmission lines are assumed to be lossless, we have
    
0i i iP P l
    
0i i iP P l
   
2 21 1
0
2 2
i i ia a x
   
2 21 1
0
2 2
i i ib b x
No power loss everywhere on the lines
   
21
0 0
2
i iP b

16/32

17. Department of Electronic Engineering, NTUT
Consider Matched Source and Load (I)
    2 2 20 0oV Z I
                    2 2 2 2 2 2 2 2
2 2
1 1
0 0 0 0 0 0
2 2
o o o
o o
a V Z I Z I Z I
Z Z
It follows that
Two-port
Network

1oZ
Port 1
1 1x l
Port 2
2 2x l
Port 1'
1 0x
 1 0I
Port 2'
2 0x
2l1l

 1 0V
 2 0I


 2 2V l
2oZ
 1 1I l  2 2I l
 1 1V l


1TZ
 2 2a x
 2 2b x
 1 1a x
 1 1b x


 2 0V


1E
1 1oZ Z
2 2oZ Z
matched
matched
No reflection from load• At x2=0, we have
         
1
1 1 1 1
1 1
1
0 0 0
2 2
o
o o
E
a V Z I
Z Z
  
2
2 1
1
1
0
4 o
E
a
Z
    1 1 1 10 0oV E Z I• At x1=0, we have
It follows that and
Vpp
17/32

18. Department of Electronic Engineering, NTUT
Consider Matched Source and Load (II)
   
  
2
2 1
1 1
1
1
0 0
2 8
AVS
o
E
P P a
Z
• Since the line is lossless, we have
   
2 2
1 1 1
1 1
0
2 2
a a l
Power available from the source is independent of
the input impedance ZT1 of the two-port network
• The power available from the source E1 with internal resistance
Z1=Zo1 is equal to the power of incident wave at x1=0:
The available power PAVS is the incident power at x1=0.
18/32

19. Department of Electronic Engineering, NTUT
Mismatched Source (I)
 
       2 1 1 1 1 1 1
1
1
0 0 0 01
0
2 8
o o
o
V Z I V Z I
a
Z

       
                  
2 22
1 1 1 1 1 1 1 1 1
1
1
0 0 0 0 0 0
8
o o o
o
V Z I V Z V I Z I
Z
                    
2 2 22
1 1 1 1 1 1 1 1 1 1
1
1 1
0 0 0 0 0 0 0
2 8
o o o
o
b V Z I V Z I V Z I
Z
              
     
2 2
1 1 1 1 1 1 1
1 1 1
0 0 0 0 0 0 0
2 2 4
P a b I V I V
    
 1 1
1
Re 0 0
2
I V
• Consider that if Z1 is not equal to Zo1
Similarly,
• Power delivered to port 1', or to port 1 (since the line is lossless) is
19/32

20. Department of Electronic Engineering, NTUT
Mismatched Source (II)
    
2
1 1
1
0 0
2
AVSb P P
   l l 
2
1 1 1 1
1
2
AVSb P P
     l  
2
1 1 1 1
1
0 0
2
AVSP P P b
                       2 2 2 2 2 2 2 2 2 2
2 2
1 1
0 0 0 0 0 0
2 2
o o o o
o o
b V Z I Z I Z I Z I
Z Z
• Reflected power from port 1 (or port 1')
It can also be written as
• If ZT1=Zo1, then the reflected power is zero. However, if ZT1≠Zo1, part of
the incident power is reflected back to the generator. The net power
delivered to port 1 is
We can obtain
20/32

21. Department of Electronic Engineering, NTUT
Calculation of S11 and S21 (I)
      
2 2
2 2 2 2
1 1
0 0 0
2 2
oP b I Z
 
   
 
   l l
l l
l l 


 
 
2 2 2 2
1 1 1 1
11
1 1 1 10 0a V
b V
S
a V



1 1
11
1 1
T o
T o
Z Z
S
Z Z
• Power delivered to the load Z2 (=Zo2)
• Calculate the S-parameter
S11 is the reflection coefficient of port 1 with port 2 terminated in its
normalizing impedance Zo2. (a2=0)
• The evaluation of S11 at x1=0 (S'11) can be done using .
Alternately, we can calculate the input impedance at x1=0, and its
associated reflection coefficient would be S'11.
12
11 11
j
S S e 
  l
21/32

22. Department of Electronic Engineering, NTUT
Calculation of S11 and S21 (II)
 
   
 
l
l l
l


 
2 2
2
2 1 1 1 1
11 2
1 1
0
AVS
AVS
a
b P P
S
Pa
     l   
2
1 1 1 110 1AVSP P P S
 
   
 
   l l
l l
l l 


 
 
2 2 2 2
2 2 2 2 1
21
1 1 1 1 10 0
o
oa I
b Z I
S
a Z I
 
   l
l
l 




2 2
2 2 2
1 1 1 0
o
o I
Z I
Z I
• The ratio of the power reflected from port 1 to the power available at
port 1.
or
• If , the power reflected is larger than the power available at
port 1. In this case, port 1 acts as a source of power and oscillations
can occur.
• Evaluation of S21 at unprimed reference plane
            
      2 2 2 2 2 2 2 2 2 2since 0I I I I Il l l l l
11 1S 
22/32

23. Department of Electronic Engineering, NTUT
Find S Parameter by Excitation (I)
• Thevenin’s equivalent network

 1
1, 1
j
THE E e l
Two-port
Network
Port 1
1 1x l
Port 2
2 2x l


 2 2V l
 1 1I l  2 2I l
 1 1V l


1TZ
  2 2 0a l
 2 2b l
 1 1a l
 1 1b l


1,THE
1oZ
2oZ
Two-port
Network

1oZ
Port 1
1 1x l
Port 2
2 2x l
Port 1'
1 0x
 1 0I
Port 2'
2 0x
2l1l

 1 0V
 2 0I


 2 2V l
2oZ
 1 1I l  2 2I l
 1 1V l


1TZ
 2 2a x
 2 2b x
 1 1a x
 1 1b x


 2 0V


1E
1 1oZ Z
2 2oZ Z
matched
matched
23/32

24. Department of Electronic Engineering, NTUT
Find S Parameter by Excitation (II)
 
 
   
l
l l l
    
1 1
1 1 1 1 1 1 1
11
1
2
o
oo
a
I V Z I
ZZ
• Thevenin’s equivalent network
Two-port
Network
Port 1
1 1x l
Port 2
2 2x l


 2 2V l
 1 1I l  2 2I l
 1 1V l


1TZ
  2 2 0a l
 2 2b l
 1 1a l
 1 1b l


1,THE
1oZ
2oZ
   l l 1 1 1, 1 1 1TH oV E Z I
 l
 1,
1 1
12
TH
o
E
I
Z
 
 l
l  2 2
2 2
2o
V
I
Z
 
   
 
2 2
2 2 2 2 21
21
1,1 1 1 20
2o o
THo oI
Z I VZ
S
EZ I Z



 
l
l l
l
• At port 1:
• At port 2:
• The S21:
S21 represents a forward voltage
transmission coefficient from
port 1 to port 2.
24/32

25. Department of Electronic Engineering, NTUT
Find S Parameter by Excitation (III)
 
2
2 2
22
212
1,
1
1
2
8
o
T
TH
o
V
Z
G S
E
Z
 
l

 
 
 
2
21
1,
2
TH
V
S
E  
2
2 2
21
1, 2
L
T
AVS TH
P V
G S
P E
  
GT represents the ratio of the power delivered to the load Zo2 (i.e., PL) to the
power available from the source E1,TH (i.e., PAVS).
• If Z1 = Z2 = Zo
• Transducer Power Gain:
2
21TG S
and
25/32

26. Department of Electronic Engineering, NTUT
Find S Parameter by Excitation (IV)
 
   

 

1 1
2 2 2 2
22
2 2 2 20
T o
T oa
b Z Z
S
a Z Zl
l
l
 
   
 

 
1 1
1 1 2 1 1
12
2 2 1 2,0
2 o
o THa
b Z V
S
a Z El
l l
l
• Excitation at port2’ by E2 with source impedance Z2=Zo2 is placed at port 2’ and
port 1’ is matched (Z1=Zo1) we find that at the unprimed reference planes
S22 is the reflection coefficient of port 2 with port 1 terminated in its
normalizing impedance Z1= Zo1. (a1(l1)=0) , and S12 represents a reverse
voltage evaluate S’22 and S’12 at the primed reference planes.
Two-port
Network1oZ
Port 1
1 1x l
Port 2
2 2x l
Port 1'
1 0x
Port 2'
2 0x
2l1l
2oZ
2TZ
 2 2a l
 2 2b l
  1 1 0a l
 1 1b l


2E
2 2oZ Z
1 1oZ Z
26/32

27. Department of Electronic Engineering, NTUT
Find S Parameter by Excitation (V)
 
2
1 1
2 1
12 2
2,
2
1
2
8
o
TH
o
V
Z
S
E
Z

l
The S parameter of a transistor are commonly ,measured with Zo1=Zo2=Zo
and Z1 = Z2 = Zo. These S parameters are said to be measured in a Zo system.
If this transistor is then used in the circuit with arbitrary terminations Z1 and
Z2, the gain GT is no longer as given. GT can be expressed in terms of Z1, Z2,
and the S parameters of the transistor measured in a Zo system.
• Reverse Transducer Power Gain:
27/32

28. Department of Electronic Engineering, NTUT
Example – S Parameter of a Series Z (I)
• Evaluate the S parameters, in a Zo system, of a series impedance Z.
Z
oZ
Port 1
1 1x l
Port 2
2 2x l
Port 1'
1 0x
Port 2'
2 0x
oZ
1TZ
 2 2a l
 2 2b l
 1 1a l
 1 1b l


1E
1 oZ Z
2 oZ Z
matched
matched
Z
Port 1 Port 2
28/32

29. Department of Electronic Engineering, NTUT
Example – S Parameter of a Series Z (II)
• Thevenin’s equivalent network
 
   2 2
1 1 1
11
1 1 10
T o
T oa
b Z Z
S
a Z Z

 
l
l
l
1T oZ Z Z where 11
2 o
Z
S
Z Z


Z
Port 1 Port 2
1TZ
 1 1a l
 1 1b l


1,THE
oZ
oZ


 2 2V l
 2 2 1,
2
o
TH
o
Z
V E
Z Z


l
 
   
1,
2 2
21
1, 1,
2 2
22 2
o
TH
o o
oTH TH
Z
E
V Z Z Z
S
Z ZE E

  

l
(1)
(2)
For symmetry, we observe that S22=S11 and S12 =S21. (Reciprocal condition)
• For , and in a system:100Z j  50  
0.707 45 0.707 45
0.707 45 0.707 45
S
   
  
   
29/32

30. Department of Electronic Engineering, NTUT
Example – S Parameter of a Shunt Y (I)
• Evaluate the S parameters, in a Zo system, of a shunt admittance Y.
oZ
Port 1
1 1x l
Port 2
2 2x l
Port 1'
1 0x
Port 2'
2 0x
oZ
1TZ
 2 2a l
 2 2b l
 1 1a l
 1 1b l


1E
1 oZ Z
2 oZ Z
matched
matched
Y
Port 1 Port 2
Y
30/32

31. Department of Electronic Engineering, NTUT
Example – S Parameter of a Shunt Y (II)
• Thevenin’s equivalent network
 
   2 2
1 1 1
11
1 1 10
T o
T oa
b Z Z
S
a Z Z

 
l
l
l
1
1
||
1
o
T o
o
Z
Z Z
Y Z Y
 

where 11
2
o
o
Z Y
S
Z Y



Port 1 Port 2
1TZ
 1 1a l
 1 1b l


1,THE
oZ
oZ


 2 2V l
  1,1
2 2 1,
1 2
THT
TH
T o o
EZ
V E
Z Z Z Y
 
 
l
 
 
2 2
21
1,
2
22 oTH
V
S
Z YE
 

l
(1)
(2)
For symmetry, we observe that S22=S11 and S12 =S21. (Reciprocal condition)
• For , and in a system:10 mSY  50  
0.2 0.8
0.8 0.2
S
 
   
Y
31/32

32. Department of Electronic Engineering, NTUT
Summary
• For a 2-port network:   11 12
21 22
S S
S
S S
 
  
 
     l   
2
1 1 1 110 1AVSP P P S
   

21
0 0
2
i iP a
   
21
0 0
2
i iP b

• Average incident power:
• Average reflected power:
 With lossless lines:
       
2 21 1
0 0
2 2
i i i i i iP P x a a x 
  
       
2 21 1
0 0
2 2
i i i i i iP P x b b x 
  
   
2
1 1
1
0 0
2
AVSP P a
 • Available power from source:
 With matched condition:    
  
2
2 1
1 1
1
1
0 0
2 8
AVS
o
E
P P a
Z
       
2 2 2
1 1 1 1
1 1 1
0 0 0 0
2 2 2
AVSP a b P b   • Power delivered to port 1:
 With lossless lines:
32/32