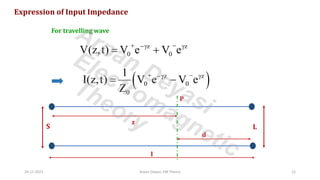
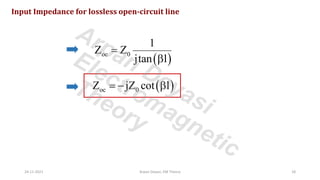
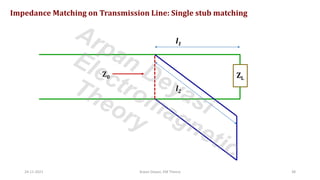
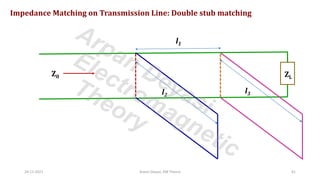
The document discusses transmission line impedance and input impedance. It defines characteristic impedance as the ratio of voltage to current waves travelling along a transmission line. It provides expressions for characteristic impedance in terms of line parameters R, L, G, C. It then derives expressions for input impedance of open circuit, short circuit, matched and mismatched lossless transmission lines. It shows that input impedance is capacitive for a short open circuit line and inductive for a short circuit line.

1. Course: Electromagnetic Theory
paper code: EI 503
Course Coordinator: Arpan Deyasi
Department of Electronics and Communication Engineering
RCC Institute of Information Technology
Kolkata, India
Topic: Transmission Line – Impedance
24-11-2021 Arpan Deyasi, EM Theory 1
Arpan Deyasi
Electromagnetic
Theory

2. Characteristic Impedance
It is the ratio of voltage wave travelling in positive direction to the current
wave along same direction, measured at any point in the transmission line
0
0
0
V
Z
I
+
+
=
Similarly, it is the negative ratio of voltage wave travelling in negative
direction to the current wave along same direction, measured at any point
in the transmission line
0
0
0
V
Z
I
−
−
= −
24-11-2021 Arpan Deyasi, EM Theory 2
Arpan Deyasi
Electromagnetic
Theory

3. Expression of Characteristic Impedance
From transmission line equation
V(z,t) RI(z,t) L I(z,t)
z t
 
− = +
 
Substituting j
t

 

( )
V(z,t) R j L I(z,t)
z

− = + 

Now z z
0 0
V(z,t) V e V e
+ −
− 
= +
…………….. (1)
24-11-2021 Arpan Deyasi, EM Theory 3
Arpan Deyasi
Electromagnetic
Theory

4. Expression of Characteristic Impedance
( )
z z
0 0
V(z,t) V e V e
z
+ −
− 

= − −

…………….. (2)
Substituting in (1)
( ) ( )
z z
0 0
R j L I(z,t) V e V e
+ −
− 
+  =  −
( )
( )
z z
0 0
I(z,t) V e V e
R j L
+ −
− 

= −
+ 
( )
( )
( )
z z
0 0
G j C
I(z,t) V e V e
R j L
+ −
− 
+ 
= −
+ 
24-11-2021 Arpan Deyasi, EM Theory 4
Arpan Deyasi
Electromagnetic
Theory

5. Expression of Characteristic Impedance
( ) ( )
( )
z z
0 0
R j L
V e V e I(z,t)
G j C
+ −
−  + 
− =
+ 
( )
z z
0 0 0
V e V e I(z,t)Z
+ −
− 
− =
where
( )
( )
0
R j L
Z
G j C
+ 
=
+ 
24-11-2021 Arpan Deyasi, EM Theory 5
Arpan Deyasi
Electromagnetic
Theory

6. Characteristic Impedance for Distortionless Line
( )
( )
0
R j L
Z
G j C
+ 
=
+ 
0
L
R 1 j
R
Z
C
G 1 j
G
 
+ 
 
 
=
 
+ 
 
 
LG RC
=
For distortionless line
0
R L
Z
G C
 = =
24-11-2021 Arpan Deyasi, EM Theory 6
Arpan Deyasi
Electromagnetic
Theory

7. A transmission line with air dielectric has characteristic impedance 60 Ω and
phase constant 4 rad/m at 500 MHz. Calculate inductance and capacitance.
Problem 1
Soln
0
L
Z
C
=
LC
 = 
0
Z 1
C
 =
 
24-11-2021 Arpan Deyasi, EM Theory 7
Arpan Deyasi
Electromagnetic
Theory

8. 0
C 21.2 pF/m
Z

= =

2
0
L Z C 334.2 mH/m
= =
24-11-2021 Arpan Deyasi, EM Theory 8
Arpan Deyasi
Electromagnetic
Theory

9. A distortionless line has Z0 = 60 Ω, α = 20 mNp/m, u = 0.6c. Find R, L, G, C at 100
MHz.
Problem 2
Soln
0
L
Z 60
C
= =
3
C
R 20 10
L
−
 = = 
R 1.2 /m
 = 
24-11-2021 Arpan Deyasi, EM Theory 9
Arpan Deyasi
Electromagnetic
Theory

10. 8
p
1
v 0.6 3 10
LC
= =  
0
L
Z 60
C
= =
L 333.3 nH/m
 =
& C 92.59 pF/m
=
24-11-2021 Arpan Deyasi, EM Theory 10
Arpan Deyasi
Electromagnetic
Theory

11. 0
R
Z 60
G
= =
R 1.2 /m
= 
G 333.3 S/m
 = 
24-11-2021 Arpan Deyasi, EM Theory 11
Arpan Deyasi
Electromagnetic
Theory

12. Expression of Input Impedance
For travelling wave
z z
0 0
V(z,t) V e V e
+ −
− 
= +
( )
z z
0 0
0
1
I(z,t) V e V e
Z
+ −
− 
= −
S L
P
z
d
l
24-11-2021 Arpan Deyasi, EM Theory 12
Arpan Deyasi
Electromagnetic
Theory

13. Expression of Input Impedance
( )
( )
z z
0 0
P
P 0 z z
P 0 0
V e V e
V
Z Z
I V e V e
+ −
− 
+ −
− 
+
= =
−
Substituting z l d
= −
l d l d
0 0
P 0 l d l d
0 0
V e e V e e
Z Z
V e e V e e
+ −
−   −
+ −
−   −
+
=
−
d d
l
P 0 d d
l
e e
Z Z
e e
 −
 −
+ 
=
− 
24-11-2021 Arpan Deyasi, EM Theory 13
Arpan Deyasi
Electromagnetic
Theory

14. d d
L 0
L 0
P 0
d d
L 0
L 0
Z Z
e e
Z Z
Z Z
Z Z
e e
Z Z
 −
 −
 
−
+  
+
 
=
 
−
−  
+
 
Expression of Input Impedance
( ) ( )
( ) ( )
d d
L 0 L 0
P 0 d d
L 0 L 0
Z Z e Z Z e
Z Z
Z Z e Z Z e
 −
 −
+ + −
=
+ − −
( ) ( )
( ) ( )
d d d d
L 0
P 0 d d d d
L 0
Z e e Z e e
Z Z
Z e e Z e e
 −  −
 −  −
+ + −
=
+ − −
24-11-2021 Arpan Deyasi, EM Theory 14
Arpan Deyasi
Electromagnetic
Theory

15. Expression of Input Impedance
( ) ( )
( ) ( )
L 0
P 0
0 L
Z cosh d Z sinh d
Z Z
Z cosh d Z sinh d
 + 
=
 + 
( )
( )
L 0
P 0
0 L
Z Z tanh d
Z Z
Z Z tanh d
+ 
=
+ 
Replacing ‘d’ by ‘l’
( )
( )
L 0
in 0
0 L
Z Z tanh l
Z Z
Z Z tanh l
+ 
=
+ 
24-11-2021 Arpan Deyasi, EM Theory 15
Arpan Deyasi
Electromagnetic
Theory

16. Input Impedance for lossless line
For lossless transmission line
0, j
 =  = 
( )
( )
L 0
in 0
lossless
0 L
Z Z tanh j l
Z Z
Z Z tanh j l
+ 
 =
+ 
( )
( )
L 0
in 0
lossless
0 L
Z jZ tan l
Z Z
Z jZ tan l
+ 
=
+ 
24-11-2021 Arpan Deyasi, EM Theory 16
Arpan Deyasi
Electromagnetic
Theory

17. Input Impedance for lossless open-circuit line
For open-circuit line
L
Z →
( )
( )
L 0
inll oc 0
o.c
0 L
Z jZ tan l
Z Z Z
Z jZ tan l
+ 
 = =
+ 
( )
( )
0
L
oc 0
0
L
Z
1 j tan l
Z
Z Z
Z
jtan l
Z
+ 
=
+ 
24-11-2021 Arpan Deyasi, EM Theory 17
Arpan Deyasi
Electromagnetic
Theory

18. Input Impedance for lossless open-circuit line
( )
oc 0
1
Z Z
jtan l
=

( )
oc 0
Z jZ cot l
= − 
24-11-2021 Arpan Deyasi, EM Theory 18
Arpan Deyasi
Electromagnetic
Theory

19. Input Impedance for lossless open-circuit line with small length
( )
oc 0
s
Z jZ cot l
= − 
0
oc s
jZ
Z
l
= −

( )
oc s
L
j
C
Z
LC l
= −

oc s
1
Z
j Cl
=

So, input impedance for lossless open-circuit transmission line
with small length is capacitive in nature
24-11-2021 Arpan Deyasi, EM Theory 19
Arpan Deyasi
Electromagnetic
Theory

20. Input Impedance for lossless short-circuit line
For short-circuit line
L
Z 0
=
( )
( )
L 0
inll sc 0
s.c
0 L
Z jZ tan l
Z Z Z
Z jZ tan l
+ 
 = =
+ 
( )
0
sc 0
0
jZ tan l
Z Z
Z

=
( )
sc 0
Z jZ tan l
= 
24-11-2021 Arpan Deyasi, EM Theory 20
Arpan Deyasi
Electromagnetic
Theory

21. Input Impedance for lossless short-circuit line with small length
( )
sc 0
s
Z jZ tan l
= 
( )
sc 0
s
Z jZ l
= 
( )
sc s
L
Z j LC l
C
= 
sc s
Z j Ll
= 
So, input impedance for lossless short-circuit transmission line
with small length is inductive in nature
24-11-2021 Arpan Deyasi, EM Theory 21
Arpan Deyasi
Electromagnetic
Theory

22. Problem 3
Find the input impedance of (λ/8) short circuited lossless transmission line
Soln
( )
( )
L 0
in 0
0 L
Z Z tanh l
Z Z
Z Z tanh l
+ 
=
+ 
For short-circuited line
L
Z 0
=
( )
0
in 0
0
Z tanh l
Z Z
Z

=
24-11-2021 Arpan Deyasi, EM Theory 22
Arpan Deyasi
Electromagnetic
Theory

23. ( )
in 0
Z Z tanh l
= 
( )
in 0 0 0
2
Z Z tanh j l Z tanh j Z tanh j
8 4
  
   
 =  = =
   

   
j j
4 4
0 0
j j
4 4
cos jsin cos jsin
e e 4 4 4 4
Z Z
cos jsin cos jsin
e e
4 4 4 4
 
−
 
−
   
   
+ − −
   
−    
= =
   
   
+ + −
+    
   
0 0
2jsin
4
Z Z j
2cos
4

= =
 in 0
Z jZ
=
24-11-2021 Arpan Deyasi, EM Theory 23
Arpan Deyasi
Electromagnetic
Theory

24. Input Impedance for lossless matched line
For matched line
L 0
Z Z
=
( )
( )
L 0
inll mc 0
m.c
0 L
Z jZ tan l
Z Z Z
Z jZ tan l
+ 
 = =
+ 
mc 0
Z Z
=
24-11-2021 Arpan Deyasi, EM Theory 24
Arpan Deyasi
Electromagnetic
Theory

25. Input Impedance for lossless matched line
mc 0
Z Z
=
( )
oc 0
Z jZ cot l
= − 
( )
sc 0
Z jZ tan l
= 
mc 0 oc sc
Z Z Z Z
= =
24-11-2021 Arpan Deyasi, EM Theory 25
Arpan Deyasi
Electromagnetic
Theory

26. Full wave lossless transmission line
l n
= 
2 2
l l n 2n
 
  = =  = 
 
( )
tan l 0
 =
( )
( )
L 0
in 0
0 L
Z Z tan l
Z Z
Z Z tan l
+ 
=
+ 
24-11-2021 Arpan Deyasi, EM Theory 26
Arpan Deyasi
Electromagnetic
Theory

27. Full wave lossless transmission line
L
in 0
0
Z
Z Z
Z
=
in L
Z Z
=
So, input impedance for lossless full-wave transmission line is equal to load impedance
24-11-2021 Arpan Deyasi, EM Theory 27
Arpan Deyasi
Electromagnetic
Theory

28. n
l
2

=
2 2 n
l l n
2
  
  = = = 
 
( )
tan l 0
 =
( )
( )
L 0
in 0
0 L
Z jZ tan l
Z Z
Z jZ tan l
+ 
=
+ 
Half wave lossless transmission line
24-11-2021 Arpan Deyasi, EM Theory 28
Arpan Deyasi
Electromagnetic
Theory

29. Half wave lossless transmission line
L
in 0
0
Z
Z Z
Z
=
in L
Z Z
=
So, input impedance for lossless half-wave transmission line is equal to load impedance
24-11-2021 Arpan Deyasi, EM Theory 29
Arpan Deyasi
Electromagnetic
Theory

30. Quarter wave lossless transmission line
n
l
4

=
2 2 n n
l l
4 2
   
  = = =
 
( )
tan l
 →
( )
( )
L 0
in 0
0 L
Z jZ tan l
Z Z
Z jZ tan l
+ 
=
+ 
24-11-2021 Arpan Deyasi, EM Theory 30
Arpan Deyasi
Electromagnetic
Theory

31. Quarter wave lossless transmission line
( )
( )
L
0
in 0
0
L
Z
jZ
tan l
Z Z
Z
jZ
tan l
+

=
+

2
0
in
L
Z
Z
Z
=
0 in L
Z Z Z
=
24-11-2021 Arpan Deyasi, EM Theory 31
Arpan Deyasi
Electromagnetic
Theory

32. If 120 Ω load is to be matched to 75 Ω line, then calculate characteristic impedance
of quarter-wave transformer
Problem 4
Soln
0 in L
Z Z Z
=
0
Z 120 75
= 
0
Z 120 75
= 
0
Z 94.86
= 
24-11-2021 Arpan Deyasi, EM Theory 32
Arpan Deyasi
Electromagnetic
Theory

33. 24-11-2021 Arpan Deyasi, EM Theory 33
Impedance Matching on Transmission Line: Quarter-wave Transformer
Input impedance of a lossless line
( )
( )
L 0
in 0
lossless
0 L
Z jZ tan l
Z Z
Z jZ tan l
+ 
=
+ 
For quarter-wave line
l
4

=
2
l .
4 2
  
  = =

Arpan Deyasi
Electromagnetic
Theory

34. 24-11-2021 Arpan Deyasi, EM Theory 34
2
0
in lossless
L
Z
Z
Z
 =
in 0
0 L
Z Z
Z Z
=
in
L
1
Z
Z
=
Impedance Matching on Transmission Line: Quarter-wave Transformer
Arpan Deyasi
Electromagnetic
Theory

35. 24-11-2021 Arpan Deyasi, EM Theory 35
Impedance Matching on Transmission Line: Quarter-wave Transformer
1. Normalized input impedance of a λ/4 transmission line is equal to the reciprocal of
normalized terminating impedance. Therefore, a quarter-wave section can be considered
as impedance converter between high to low and vice-versa.
2. Short-circuited λ/4 transmission line has infinite input impedance.
3. Open-circuited λ/4 transmission line has zero input impedance.
Drawback of this technique is that it needs special line of characteristics
impedance for every pair of resistances to be matched.
Arpan Deyasi
Electromagnetic
Theory

36. 24-11-2021 Arpan Deyasi, EM Theory 36
Stub
A stub is a short-circuited section of a transmission line connected in parallel to the
main transmission line.
A stub of appropriate length is placed at some distance from the load such that the
impedance seen beyond the stub is equal to the characteristic impedance.
Use of stub
Stubs can be used to match a load impedance to the transmission line characteristic
impedance
Arpan Deyasi
Electromagnetic
Theory

37. 24-11-2021 Arpan Deyasi, EM Theory 37
Impedance Matching on Transmission Line: Single stub matching
The single-stub matching technique is superior to the quarter wavelength
transformer as it makes use of only one type of transmission line for the main
line as well as the stub.
This technique also in principle is capable of matching any complex load to the
characteristic impedance/admittance.
The single stub matching technique is quite popular in matching fixed
impedances at microwave frequencies.
Arpan Deyasi
Electromagnetic
Theory

38. 24-11-2021 Arpan Deyasi, EM Theory 38
Impedance Matching on Transmission Line: Single stub matching
ZL
Z0
l1
l2
Arpan Deyasi
Electromagnetic
Theory

39. 24-11-2021 Arpan Deyasi, EM Theory 39
Impedance Matching on Transmission Line: Single stub matching
Suppose we have a load impedance ZL connected to a transmission line with
characteristic impedance Z0
The objective here is that no reflection should be seen by the generator. In other
words, even if there are standing waves in the vicinity of the load , the standing
waves must vanish beyond certain distance from the load.
Conceptually this can be achieved by adding a stub to the main line such that the
reflected wave from the short-circuit end of the stub and the reflected wave from
the load on the main line completely cancel each other.
Arpan Deyasi
Electromagnetic
Theory

40. 24-11-2021 Arpan Deyasi, EM Theory 40
Impedance Matching on Transmission Line: Single stub matching
The single stub matching technique although has overcome the drawback of the
quarter wavelength transformer technique, it still is not suitable for matching
variable impedances.
A change in load impedance results in a change in the length as well as the location
of the stub.
Even if changing length of a stub is a simpler task, changing the location of a stub
may not be easy in certain transmission line configurations.
Drawbacks Arpan Deyasi
Electromagnetic
Theory

41. 24-11-2021 Arpan Deyasi, EM Theory 41
Impedance Matching on Transmission Line: Double stub matching
ZL
Z0
l1
l3
l2
Arpan Deyasi
Electromagnetic
Theory

42. 24-11-2021 Arpan Deyasi, EM Theory 42
Impedance Matching on Transmission Line: Double stub matching
The technique uses two stubs with fixed locations.
As the load changes only the lengths of the stubs are adjusted to achieve matching.
Let us assume that a normalized admittance is to be matched using the double stub
matching technique. The first stub is located at a convenient distance from the load.
The second stub is located at a distance of 3λ/8 rom the first stub.
Arpan Deyasi
Electromagnetic
Theory