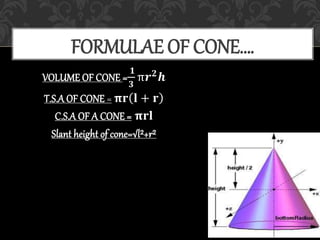
This document provides information about mensuration and different shapes used in mensuration. It defines mensuration as the assignment of numbers to measurements of objects or events. It then discusses different measurement systems like the metric system and imperial system. It provides details on common 3D shapes like cubes, cuboids, cylinders, cones, spheres, and hemispheres. For each shape, it lists key properties and provides formulas to calculate volume, total surface area, curved surface area, and other measurements.

1. MADE BY-NIKUND JAIN
CLASS-9TH-C
ROLL NO.-12
A PRESENTATIONON
MENSURATION

2. Mensuration comes from the word measurement which is the
assignment of a number to a characteristic of an object or event, which
can be compared with other objects or events. The scope and
application of a measurement is dependent on the context and
discipline. In the natural sciences and engineering, measurements do
not apply to nominal properties of objects or events.
WHATIS MENSURATION?.......

3. Before SI units were widely adopted around the world, the British systems
of English unitsand later imperial units were used in Britain,
the Commonwealth and the United States. The metric system is a
decimal systems of measurement based on its units for length, the metre and
for mass, the kilogram. It exists in several variations, with different choices
of base units, though these do not affect its day-to-day use. Since the 1960s,
the International System of Units (SI) is the internationally recognised metric
system.
DIFFERENTUNITSANDSYSTEMS….

4. CUBE
CUBOID
CYLINDER
CONE
SPHERE
HEMISPHERE etc.
DIFFERENTSHAPESUSEDIN MENSURATION…..

5. A cube is a three-dimensional solid object bounded by
six square faces, facets or sides, with three meeting at
each vertex.
The cube is the only regular hexahedron and is one of
the five Platonic solids. It has 12 edges, 6 faces and 8
vertices.
The cube is also a square parallelepiped, an
equilateral cuboid and a right rhombohedron. It is a
regular square prism in three orientations, and
a trigonal trapezohedron in four orientations.
CUBE

6. VOLUME OF CUBE = 𝒂 𝟑
VOLUME OF CUBE = 𝒂 𝟑
DIAGONAL OF A CUBE =√𝟑𝒂
T.S.A OF CUBE = 6 𝒂 𝟐
C.S.A OF A CUBE = 4 𝒂 𝟐
C.S.A OF A CUBE = 4 𝒂 𝟐
FORMULAE OF CUBE

7. A cuboid is a 3D shape. Cuboids have six faces, which form
a convex polyhedron. Simply speaking, cuboids are made
from 6 rectangles, which are placed at right angles.
Properties of a Cuboid are:
It has 12 edges
It has 8 corners or vertices
It has 6 faces.
The basic difference between a rectangle and a cuboid is
that one is a 2D shape and the other is a 3D shape.
CUBOID

8. VOLUME OF CUBOID = L*B*H
T.S.A OF CUBOID =2(l*b+b*h+h*l)
C.S.A OF A CUBOID =2h(l+b)
Diagonal of a cuboid=√l²+b²+H²
FORMULAE OF CUBOID….

9. A cylinder is one of the most basic curved geometric shapes, with
the surfaceformed by the points at a fixed distance from a
given line segment, known as the axis of the cylinder. The shape
can be thought of as a circular prism. Both the surface and the
solid shape created inside can be called a cylinder. The surface
area and the volume of a cylinder have been known since ancient
times.
In differential geometry, a cylinder is defined more broadly as any
ruled surface which is spanned by a one-parameter family
of parallel lines. A cylinder whose cross section is
an ellipse, parabola, or hyperbola is called an elliptic
cylinder, parabolic cylinder, or hyperbolic cylinder respectively.
CYLINDER

10. VOLUME OF cylinder = π 𝒓 𝟐
𝒉
T.S.A OF cylinder =2𝝅𝒓(𝒓 + 𝒉)
C.S.A OF A cylinder = 2𝝅𝒓𝒉
FORMULAE OF CYLINDER…..

11. A cone is a three-dimensional geometric shape that tapers
smoothly from a flat base (frequently, though not
necessarily, circular) to a point called the apex or vertex.
A cone is formed by a set of line segments, half-lines,
or lines connecting a common point, the apex, to all of the
points on a base that is in a plane that does not contain the
apex.
CONE

12. VOLUME OF CONE =
𝟏
𝟑
π𝒓 𝟐
𝒉
T.S.A OF CONE = 𝛑𝐫 𝐥 + 𝐫
C.S.A OF A CONE = 𝛑𝐫𝐥
Slant height of cone=√l²+r²
FORMULAE OF CONE….

13. A sphere is a perfectly round geometrical object in three-
dimensional space that is the surface of a completely round ball.
Like a circle, which geometrically is a two-dimensional object, a
sphere is defined mathematically as the set of points that are all at
the same distance r from a given point, but in three-dimensional
space. This distance r is the radius of the ball, and the given point
is the center of the mathematical ball. The longest straight line
through the ball, connecting two points of the sphere, passes
through the center and its length is thus twice the radius; it is
a diameter of the ball.
SPHERE

14. VOLUME OF SPEHERE =
𝟏
𝟑
𝝅𝒓 𝟑
S.A OF A SPEHERE =𝟒𝛑𝒓 𝟐
VOLUME OF SPERICAL SHELL ;
𝟏
𝟑
𝝅 (𝑹 𝟑-𝒓 𝟑)
FORMULAE OF SPHERE…

15. Any plane that includes the center of a sphere divides it into two
equal hemispheres. Any two intersecting planes that include the
center of a sphere subdivide the sphere into four lunes or
biangles, the vertices of which all coincide with the antipodal
points lying on the line of intersection of the planes.
The antipodal quotient of the sphere is the surface called the real
projective plane, which can also be thought of as the northern
hemisphere with antipodal points of the equator identified.
HEMISPHERE

16. VOLUME OF HEMISPEHERE =
𝟐
𝟑
𝝅𝒓 𝟑
T.S.A OF A HEMISPEHERE = 3𝛑𝒓 𝟐
C.S.A. OF HEMISPERE = 2𝛑𝒓 𝟐
FORMULAE OF HEMISPHERE